Подходы к понятию вектор

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Различные подходы к введению понятия вектора

Вектор — одно из фундаментальных понятий современной математики, оно широко используется в различных её областях. В работах Г. Бесселя,

Ж. Аргана и К. Ф. Гаусса по теории комплексных чисел установлена связь между арифметическими операциями над комплексными числами и геометрическими операциями над векторами в двумерном пространстве. В работах В. Гамильтона, Г. Грассмана, Ф. Мёбиуса понятие вектора нашло широкое применение при изучении свойств трёхмерного и многомерного пространств.

В настоящее время на векторной основе излагаются линейная алгебра, аналитическая и дифференциальная геометрия, функциональный анализ и др.

В математике иод вектором понимают элемент векторного пространства. Векторное пространство трактуется как множество объектов, на котором введены операции сложения объектов и умножения объекта на действительное число так, что выполняются известные вам аксиомы:

• 1) внутренний закон композиции: для любых элементов я, Ъ, принадлежащих множеству V, существует единственный элемент (а+Ъ)_у принадлежащий множеству К;
• 2) закон ассоциативности: а + (Ь + с) = (а + Ъ)+с, для любых элементов а , Ь, с, принадлежащих множеству V;
• 3) закон коммутативности: а + Ъ = Ь+а, для любых элементов# ,6, принадлежащих множеству V;
• 4) для любых элементов а, Ь, принадлежащих множеству V, существует такой элемент х, принадлежащий множеству V, что а + х = b;
• 5) внешний закон композиции: дтя любого элемента а, принадлежащего множеству V и для любого элемента а, принадзежащего множеству R. существует элемент аа, принадлежащий множеству V.

• 6) закон ассоциативности для умножения: <а(3)а = а((3а), где 0 и противоположно ему, если m Достоинства трактовки вектора как направленного отрезка:

• 1) Трактовка вектора как направленного отрезка придает этим объектам и операциям над ними хорошую наглядность. Это очень важно, гак как в процессе формирования понятия большую роль играет образный компонент, поэтому желательны такие определения, которые позволяют воображению легко конструировать образы определяемых объектов. Такой вывод согласуется с результатами психологических исследований.
• 2) Трактовка вектора как направленного отрезка обычно используется в физике. Таким образом, она способствует осуществлению межпредметных связей. Следует отметить и то, что в решении геометрических задач вектор используется как направленный отрезок.

Недостатки трактовки вектора как направленного отрезка:

1) Её реализация связана с громоздкостью доказательства свойств сложения векторов и умножения вектора на число. Так, доказательство переместительного свойства сложения векторов предполагает рассмотрение двух случаев: а) векторы а и b коллинеарны; б) векторы а и b неколлинеарны. Доказательство свойства: для любых k, I и вектора a (kl)a = к(1а) требует рассмотрение четырех случаев.

Кроме того, реализация трактовки вектора как направленного отрезка отличается непоследовательностью. При этой трактовке векторы считаются равными, если они имеют одинаковую длину и направление. Такое определение нельзя считать математически корректным, так как «равные векторы» — это по существу «один и тот же вектор» (аналогично тому, как «равные числа» — по существу «одно и то же число»), тогда как направленные отрезки АВ и CD — это различные отрезки, а не один и тот же отрезок. Тем самым, приняв это определение вектора, мы отождествляем два различных (хотя и родственных) математических понятия: понятие равенства и понятие эквивалентности.

Равенство двух математических объектов есть их совпадение; эквивалентность же объектов означает любое отношение, обладающее свойствами рефлексивности, симметричности и транзитивности.

Непоследовательность такой трактовки вектора проявляется при доказательстве теорем или решении задач. Например, доказательство того, что сумма векторов зависит от выбора «начальной» точки предполагает не различать равные векторы, то есть понимать под вектором множество сонаправленных отрезков равной длины, хотя вектор определен как направленный отрезок.

Конечно, эту непоследовательность легко можно исключить, если с самого начала вектор определить как множество сонаправленных отрезков равной длины, но в этом случае наглядность затруднительна.

Трактовка вектора как параллельного переноса наиболее абстракта, лишена наглядности, неприемлема в физике. Ее достоинства — это отсутствие непоследовательностей в действиях с векторами, естественное введение сложения векторов и умножения вектора на число, более простые доказательства основных законов векторной алгебры. Ее реализация требует обширных знаний теории геометрических преобразований. Но геометрические преобразования не составляют основу наших учебников, поэтому такой подход к введению понятия вектора нс используется в настоящее время.

Трудность выбора того или иного определения вектора возникает потому, что в различных научных дисциплинах используются различные виды векторов. Так, в механике обычно рассматриваются так называемые скользящие векторы (вектор, начало которого можно выбирать на некоторой прямой, по которой он может перемещаться) и связанный вектор (вектор, начало которого отождествляется с некоторой фиксированной точкой); в математике же обычно имеют дело с так называемым свободным вектором (не связанным ни с какой прямой и ни с какой фиксированной точкой).

Итак, рассмотрение различных интерпретаций векторного пространства приводит к выводу о том, что наиболее приемлемой в средней школе является интерпретация вектора как направленного отрезка.

Следует заметить, что есть предложения отказаться в школьном курсе геометрии от определения вектора. В этом случае вектор появляется как термин, обозначающий векторные величины; направленный отрезок выступает как изображение этой величины (вектора).

Такой подход реализуется в учебнике геометрии А. Д. Александрова, А. Л. Вернера и В. И. Рыжика и в «Экспериментальном учебном пособии по математике» для ПТУ М. И. Баш макова (М., 1987).

Последовательность изучения векторных понятий в действующих учебниках геометрии представлена в таблице 14.

Л. С. Атанасян и др.

8 класс (последняя глава)

Понятие вектора, нулевой вектор, длина или модуль вектора, равные векторы, откладывание вектора от точки, сложение и вычитание векторов, умножение вектора на число

Понятие вскгора, абсолютная величина (модуль) вскгора, равные векторы, нулевой вектор, откладывание вектора от точки, координаты вектора, сложение векторов. умножение вектора на число, коллинсарныс вектора, скалярное произведение векторов.

Скалярное произведение векторов

Изложение теории векторов в учебнике А. В. Погорелова отличается от соответствующего изложения в учебнике Л. С. Атанасяна и др. не только последовательностью, но и методом изложения.

В основу изложения векторов в учебнике А. В. Погорелова положен координатный метод, поэтому здесь широко используются координатные модели векторных понятий и доказательства теорем с использованием координат вектора.

В учебнике Л. С. Атанасяна и др., а также в учебнике А. Д. Александрова и др. используется метод изложения без использования координат. Это создаст определенные трудности в обосновании законов векторной алгебры. Трудности возникают, главным образом, за счет необходимости рассмотрения большого количества частных случаев. Так, доказательство независимости суммы векторов от выбранной точки требует рассмотрения кроме стандартного случая (точки А, В,С,А, В|, С не лежат на одной прямой), который приведен в учебнике Л. С. Атанасяна и др., случая, при котором все точки Л, В, С, А₉ В_ь С расположены на одной прямой. Доказательство переместительного свойства сложения векгоров предполагает рассмотрение двух частных случаев, а доказательство сочетательного свойства умножения вектора на число — четырех случаев.

В учебнике Л. С. Атанасяна и др. большинство теорем, связанных со свойствами векторов, сообщаются без доказательства. В учебнике А.Д. Александрова и др. — все свойства обосновываются.

Тема «Векторы» как в учебнике Л. С. Атанасяна и др., так и в учебнике А. В. Погорелова, является последней в курсе геометрии 8 класса. Это, очевидно, отражает точку зрения авторов на функции векторов в изложении геометрии: им отводится, в основном, служебная роль (способствовать изучению физических векторных величин). Об этом говорит и то, что векторы никак нс связаны с изучением основного содержания курса геометрии.

В действующих учебниках геометрии вектор трактуется как направленный отрезок. При введении понятия вектора следует обратить внимание на понимание различия между отрезком и направленным отрезком. Ученики должны усвоить, что отрезок АВ и отрезок В А — один и тот же объект, направленный отрезок АВ и направленный отрезок ВА — разные объекты. Для этого можно использовать упражнения.

• 1. Сколько отрезков и сколько векторов определяют две (три) различные точки?
• 2. Начертите параллелограмм. Назовите все отрезки, концами которых являются вершины параллелограмма. Назовите все векторы, определяемые вершинами параллелограмма. И т. д.

Видео:8 класс, 40 урок, Понятие вектораСкачать

Различные подходы к определению понятия вектора в математике и в школьном курсе математики

Различные подходы к определению понятия вектора в математике и в школьном курсе математики

Вектор является одним из фундаментальных понятий современной математики. Эволюция этого понятия осуществлялась благодаря широкому использованию его в различных областях математики, механики, а так же в технике.

Уже на уроках физики в 7 классе изложение материала ведется с широким привлечением векторного аппарата. Понятно, что это заставляет задуматься, прежде всего, над тем, как наиболее естественно ввести в курс математики средней школы понятие вектора, как эффективнее применять его при изложении теории и решении задач, как рассматривать основные действия над векторами.

Известно, что существует несколько подходов к ведению этого понятия.

В учебнике Л.Я. Куликова по алгебре [17] «n-мерным вектором над полем F (где F-поле скаляров) называется любой кортеж из n элементов поля F».

При таком подходе вектор обычно записывается в виде строки или столбца. Например, (?1, ?2,…, ?n), где ?i-скаляры.

Вводится определение равных векторов.

Определение1: Векторы (?1, ?2,…, ?n) и (?1,?2,…, ?n) называются равными, если ?i=?i, .

Так же на множестве n-мерных векторов определены операции сложения, умножения вектора на скаляр.

Определение 2: Суммой векторов (?1, ?2,…, ?n) и (?1,?2,…, ?n) называется вектор (?1+?1,?2+?2,…, ?n+?n).

Определение 3: Произведением скаляра ? на вектор (?1, ?2,…, ?n) называется вектор (??1, ??2,…, ??n).

Определение 4: Вектор (0,0,…,0) называется нулевым вектором и обозначается символом 0. Нулевой вектор является нейтральным элементом относительно сложения.

Определение 5: Вектор (-1)(?1, ?2,…, ?n) называется вектором, противоположным вектору а=(?1, ?2,…, ?n), и обозначается символом – а.

В теории линейной алгебры можно встретить другой, абстрактный подход. Например, в учебном пособии [4] вектор определяется как элемент векторного пространства V, который обладает рядом свойств:

1. () 1?=;
2. () 0?=;
3. () ??=;
4. () (-1)?= —

В данном случае определение вектора вводится аксиоматически, через систему свойств.

В качестве векторных пространств в смысле этого определения можно привести следующие:

1. V2-множество векторов на плоскости. Тогда V2- векторное пространство над |R.

2. С — векторное пространство над |R, Q. |R-векторное пространство над Q.

3. Нулевое векторное пространство V=<> над Р.(+=, ??=).

Анализируя оба подхода к определению понятия вектора, лежащих в основе линейной алгебры, можно сделать вывод, что в данном случае геометрия полностью заменяется алгеброй, а все арифметические операции над векторами сводятся к аналогичным операциям над числами.

В геометрии к определению понятия вектора другой подход:

«Вектор — геометрический объект, характеризующийся направлением и длиной».

Кроме того, существуют различные конкретизации.

I. Предметом векторного исчисления служит вектор как множество сонаправленных отрезков, имеющих одинаковую длину.

Соответственно этому подходу векторы рассматривают с точностью до их положения (т.е. не различая равных векторов, получающихся друг из друга параллельным переносом). В этом смысле векторы называют свободными. Таким образом, свободные векторы вполне определяются заданием его длины и (если он не нулевой) направления. Равные векторы, не совпадающие по положению, рассматриваются как различные конкретные изображения одного и того же свободного вектора.

Данный подход имеет ряд преимуществ. Во-первых, он упрощает понятие равенства, а во-вторых, однозначно определяет операции для свободных векторов. Так, сумма двух свободных векторов есть определенный свободный вектор, тогда как, к примеру, суммой двух направленных отрезков служит любой из направленных отрезков, полученных соответствующим построением. Тем не менее, этот подход осложняется большим числом оговорок. Например, из начального курса физики хорошо известно, что сила может быть изображена направленным отрезком. Но она не может быть изображена вектором в смысле этого определения, поскольку силы, изображаемые равными направленными отрезками, производят, вообще говоря, различные действия. (Если сила действует на упругое тело, то изображающий её отрезок не может быть перенесен даже вдоль той прямой, на которой он лежит).

II. В основу теории движения заложено понятие вектора как параллельного переноса.

Параллельным переносом называется такое движение, при котором точки смещаются по параллельным прямым на одно и то же расстояние в одном и том же направлении. Действительно, задать параллельный перенос – это все равно, что задать длину (а именно расстояние, на которое смещаются все точки) и направление (а именно, направление, в котором смещаются все точки), а задать длину и направление – все равно, что задать свободный вектор.

В этом случае сложение векторов соответствует сочетанию (композиции) параллельных переносов.

Такое определение вектора позволяет устранить противоречия с теоретико-множественной точки зрения на понятие равенства, которое возникло при традиционном определении вектора как направленного отрезка. Кроме того, такой подход к введению понятия вектора является логически безупречным, но, между тем, он недостаточно нагляден.

III. В аналитической геометрии вектор определяется как направленный отрезок.

«Пара точек называется упорядоченной, если про эти точки известно, какая из них первая, а какая-вторая» [4, с. 15].

Определение 1: Отрезок, концы которого упорядочены, называется вектором. Нулевой вектор – вектор, у которого начало и конец вектора совпадают.

Определение 2: Векторы называются коллинеарными, если существует такая прямая, которой они параллельны.

Определение 3: Расстояние между началом и концом вектора называется его длиной.

Определение 4: Два вектора называются равными, если они коллинеарные, одинаково направлены и имеют равные длины.

При данном подходе операции сложения векторов и умножения вектора на число определяются следующим образом:

Определение 5: Пусть даны 2 вектора и . Суммой называется вектор, который идет из начала вектора в конец вектора , при условии, что вектор приложен к концу вектора .

Определение 6: Пусть даны вектор и число ?. Обозначим их модули соответственно через || и |?|. Произведением ? называется вектор, который коллинеарен вектору , имеет длину, равную |?|?||, и направление такое же, как у вектора , если ?>0, и противоположное, если ?

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Вектор: определение и основные понятия

Видео:Видеоурок "Понятие вектора"Скачать

Определение вектора

рис. 1

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Обозначение вектора

Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Длина вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Нулевой вектор

Нулевой вектор обычно обозначается как 0 .

Длина нулевого вектора равна нулю.

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Коллинеарные вектора

рис. 2

Видео:Координаты вектора. 9 класс.Скачать

Сонаправленные вектора

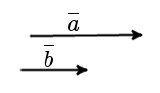рис. 3

Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Противоположно направленные вектора

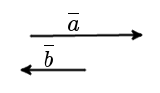рис. 4

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Компланарные вектора

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Видео:10 класс, 38 урок, Понятие вектораСкачать

Равные вектора

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Единичный вектор

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

💡 Видео

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Понятие вектора | Геометрия 7-9 класс #76 | ИнфоурокСкачать

Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Векторы для чайников (что потребуется знать при решении физических задач)Скачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать