По данным векторам а и б построить вектор а 2б (7 видео)

Для данных векторов а и Ь постройте векторы: а) а + 2b; б) ½ b — а; в) За + ½ b; г) 11/2 а – 3b.

Содержание

Ваш ответ
Похожие вопросы
По данным векторам а и б построить вектор а 2б
3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»
🌟 Видео

Видео:№776. Начертите два неколлинеарных вектора х и у и постройте векторы: a) x+2y; б) ½y + х; в) 3x+½yСкачать

Ваш ответ

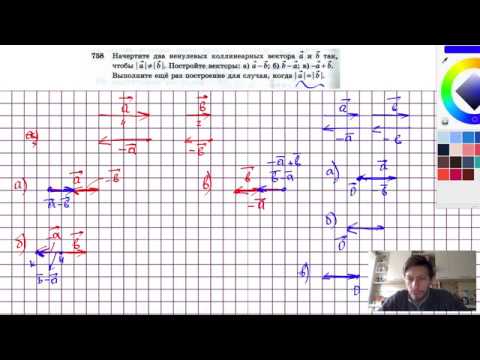
Видео:№758. Начертите два ненулевых коллинеарных вектора а и b так, чтобы | а |≠| b |. Постройте векторыСкачать

По данным векторам а и б построить вектор а 2б

Глава I. Векторы на плоскости и в пространстве

Задачи к главе I

1.1. По данным векторам а и b постройте следующие векторы:

1.2. На рис. 66 окружность разделена на три, четыре или шесть конгруэнтных дуг. Найдите в каждом случае сумму изображенных на рисунках векторов.

1.3. Для векторов а, b, с, изображенных на рис. 67, найдите сумму а + b + с.

1.4. На материальную точку действуют две силы F₁ и F₂. Найдите величину их равнодействующей, если | F₁ |=8H, | F₂ | = 6Н и (F₁; ^ F₂) = 90°.

1.5. Начертите любой пятиугольник ABCDE и найдите сумму векторов AB > , BC > , CD > , DE > , EA > .

1.6. К центру правильного шестиугольника приложены три силы, направленные в три последовательные вершины. Найдите величину равнодействующей, если величина каждой из данных сил равна 1Н.

1.7. Найдите равнодействующую трех сил, приложенных в точке М, если известно, что эти силы изображаются векторами MA > , MB > , MC > где точки А, В, С являются вершинами равностороннего треугольника, вписанного в окружность с центром О (рис. 68).

1.8. Докажите, что из медиан любого треугольника можно построить треугольник.

1.9. Дан тетраэдр ABCS. Найдите сумму векторов:
а) AB > + BC > + CS > ;
б) AC > + CS > + SA > + AB > .

1.10. Дана правильная четырехугольная пирамида ABCDS (S — вершина, О — основание высоты). Докажите, что сумма векторов OS > , DS > , BC > , SB > , AO > равна сумме векторов AS > , AD > , AB > , DA > .

1.15. На прямой взяты три точки А, В, С так, что CA > = 3 CB > Выразите вектор AB > через вектор CB > .

1.16. В прямоугольнике ABCD проведены диагонали: DB > = a ; AC > = b. Представьте векторы BC > , CB > , BD > , AD > + CD > в виде линейной комбинации векторов а и b.

1.17. В параллелограмме ABCD: AB > = a, AD > = b, О — точка пересечения диагоналей. Разложите векторы BO > , OB > , AC > и CO > по векторам а и b.

1.18. В равнобедренной трапеции ABCD величина угла BAD равна 60°,
|АВ | = | ВС | = | CD | = 2. Точки М и N — середины сторон ВС и DC. Разложите векторы AB > , CD > , BC > , AM > , AN > и MN > по векторам

1.19. На окружности с центром О даны точки А и В. Касательные к окружности в этих точках пересекаются в точке С. Разложите вектор OC > по векторам OA > и OB > , если: а) = 60°; б) =90°.

1.21. Дан треугольник ABC. Взяв за базис векторы е₁ = AB > , е₂ = AC > , найдите координаты векторов AM > , BN > , CP > в этом базисе. Точки М, N, Р — середины сторон ВС, АС, АВ треугольника.

1.22. Дан правильный шестиугольник ABCDEF.
Взяв за базис вектеры е₁ = AF > , е₂ = AC > , найдите координаты следующих векторов: а) AB > ; б) BC > ; в) CD > ; г) DE > ; д) EF > ; е) AD > ; ж) AE > ; з) FC > ; и) DB > ; к) BE > .

1.23. На плоскости дан правильный шестиугольник. Разложите по ортам i и j все векторы, изображенные на рис. 69, если | OE > | = 4.

1.24. В кубе ABCDA₁B₁C₁D₁ (рис. 70) точки М, N, Р, Q, R, S, T — середины ребер.

1.25 В прямоугольной декартовой системе координат даны точки
А (3; — 1; 2) и В (—1; 2; 2). Найдите координаты векторов AB > и BA > , их длины и координаты единичного вектора, направленного так же, как и вектор BA > .

1.26. Дан вектор а = 2i — 3j + 4k. Найдите вектор b, если | а | = | b |, абсцисса вектора b равна ординате вектора а, а ордината вектора b равна нулю.

1.27. Вычислите длины диагоналей параллелограмма, построенного на векторах
а = i + j и b = k — 2j.

1.28. Найдите проекцию вектора а на направление вектора b и проекцию вектора b на направление вектора а, если | а | = 2, | b | = 1, (a; ^ b) = 120°.

1.29. Найдите скалярное произведение векторов а и b, если | а | = 4, | b |= 6 и (a; ^ b) равен: а) 45°; б) 0°; в) 135°; г) 90°; д) 180°.

1.34. Дан вектор a = (3; —4). Найдите координаты единичных векторов, перпендикулярных вектору а.

1.35. Дан вектор с = (4; —7). Найдите координаты какого-либо вектора, перпендикулярного вектору с. Сколько решений имеет задача?

1.36. Дан вектор а = (1; 2; —3). Известно, что абсцисса перпендикулярного ему вектора b равна 3, а ордината равна 6; требуется найти аппликату вектора b.

1.37. Дан вектор a = (3; —4). Известно, что абсцисса перпендикулярного ему вектора b равна 8; определите ординату вектора b.

1.38. Дан вектор a = (5; 3). Известно, что ордината перпендикулярного ему вектора b равна 10; определите абсциссу вектора b.

1.39. Найдите значение α, при котором следующие векторы взаимно перпендикулярны:

1.40. Найдите значения α и β, при которых векторы а = (3; —1; α) и
b = (2; β; 1) взаимно перпендикулярны, если | b | = 3.

1.42. Даны два вектора: а = (3; — 1; 5) и b = (1; 2; — 3). Найдите вектор х, перпендикулярный оси Оz и удовлетворяющий условиям x • a = 9, x • b = —4.

1.43. Найдите вектор b, коллинеарный вектору а и удовлетворяющий данному условию:

1.44. Найдите вектор b, длина которого равна 50, коллинеарный вектору а и образующий острый угол с заданной осью:

1.45. Даны три вектора: а = (2; —1; 3), b = (1; —3; 2), с = (3; 2; —4). Найдите вектор х, удовлетворяющий условиям x • a = —5, x • b = —11, x • c = 20.

1.46. Найдите косинус угла между вектором а = (3; —4) и осью Ох.

1.47. Найдите косинусы углов между вектором а = (3; —4; 12) и осями координат.

1.48. Найдите угол между диагоналями параллелограмма, построенного на векторах а = 2i + j и b = — j + 2k.

1.49. Определите угол между вектором а = AB > + CD > и осью абсцисс, если
А (—2; 3), В (0; 8), С (5; 3) и D (10; 5).

1.51. В треугольнике с вершинами A (5; 0; 0), В (1; 1; 1) и С (3; — 1; 2) найдите величины углов.

1.62. Даны три последовательные вершины параллелограмма:
А (—3; —2; 0), В (3; —3; 1) и С (5; 0; 2). Найдите четвертую вершину D и угол между векторами AC > и BD > .

1.83. Дан треугольник с вершинами в точках А (3; —2; 1), В (3; 0; 2) и С (1; 2; 5). Вычислите угол между медианой [BD] и стороной [АС].

1.54. Дан четырехугольник с вершинами в точках А (2; —3; 1), В (1; 4; 0), С (—4; 1; 1) и D (— 5; —5; 3). Найдите угол между диагоналями [АС] и [BD] .

1.55. Дан треугольник с вершинами в точках А (—1; 4; 1), В (3; 4; —2) и С (5; 2; —1). Вычислите косинус угла при вершине В.

1.57. Выясните, правой или левой является тройка векторов а, b, с, если:

1.58. Найдите вектор [а; b] и изобразите его, если:

1.59. Найдите площадь параллелограмма, построенного на векторах а = (3; 4) и b = (4; — 3).

1.61. Найдите площадь треугольника с вершинами в точках А (0; 2; 6), В (4; 0; 0) и С (8; —2; 0).

1.62. Даны вершины параллелограмма: А (1; —2), В (—2; 2), С (4; 10) и D (7; 6). Вычислите его площадь и высоты.

1.63. Сила F = 2i — 3j + 4k приложена к точке M (1; 5; —2). Найдите величину момента силы F относительно начала координат.

1.68. Покажите, что объем параллелепипеда, построеннного на диагоналях граней данного параллелепипеда, имеющих общую вершину, равен удвоенному объему данного параллелепипеда.

1.69. Найдите смешанное произведение (а; b; с) векторов а = (0; 3; —1), b =(5; 0; 0),
с = (7; —2; 4).

1.70. Установите, компланарны ли векторы а = (8; 5; —13), b = (— 4; 2; 8),
с = (4; 7; —4); если векторы некомпланарны, то какую они образуют тройку правую или левую.

1.72. Найдите объем параллелепипеда, построенного на векторах
а = (1; 2; 3), b = (— 1; 3; 4), с = (2; 5; 2).

1.73. Центр тяжести однородного стержня находится в точке М (2; —4), один из его концов в точке A (—1; 1). Найдите координаты другого конца стержня.

1.74. Дан треугольник с вершинами в точках A (2; —5), В (1; —2) ; и С (4; 7). Найдите точку пересечения биссектрисы / B со сторoной AС.

1.75. Докажите, что если в правильной треугольной пирамиде SABC вершину А соединить с точкой М пересечения медиан противолежащей грани, то (AM)_|_.(BC).

1.76. В треугольнике ABC точки A₁, В₁ и C₁ — середины сторон ВС, АС, АВ, Докажите, что у треугольников ABC и A₁B₁C₁ точки пересечения медиан совпадают.

1.77. Докажите, что середины оснований трапеции и точка пересечения продолжений ее боковых сторон принадлежат одной нрямой.

1.78. Точки М и N — середины сторон АВ и CD четырехугольника ABCD. Докажите, что середины диагоналей четырехугольников AMND и BMNC являются вершинами параллелограмма или лежат на одной прямой.

1.79. Вычислите работу, совершаемую равнодействующей двух сил F₁ (5; — 1; 3) и F₂ (—3; —2; 4) при прямолинейном перемещении материальной точки из положения В (10; 8; —2) в положение С (9; 4; 1).

1.80. Сила F = 3i + k приложена к точке A (2; 1; 4). Найдите момент и величину момента этой силы относительно точки O (2; —1; 3).

1.81. К материальной точке приложены две силы F₁ и F₂, причем | F₁| + | F₂| = 4 Н и (F₁; ^ F₂) = 120°. Найдите наименьшее значение величины равнодействующей этих сил.

1.82. Определите, лежат ли в одной плоскости следующие четыре точки:

1.83. Вершины пирамиды находятся в точках A(2; 1; —1), В (3; 0; 1), С (2; —1; 3) и D (0; —7; 0). Найдите высоту пирамиды, опущенную из вершины D.

1.84. На плоскости даны четырехугольник ABCD и точка М. Докажите, что точки, симметричные точке М относительно середин сторон данного четырехугольника, являются вершинами параллелограмма.

1.85. Докажите, что высоты произвольного треугольника пересекаются в одной точке.

1.86. Докажите, что для взаимной перпендикулярности диагоналей четырехугольника необходимо и достаточно, чтобы суммы квадратов длин его прoтивоположных сторон были равны.

1.87. Велосипедист едет со скоростью 15 км/ч в северном направлении и ему кажется, что ветер (который дует со скоростью 9 км/ч откуда-то с северо-востока) направлен под углом 15° к линии его движения. Найдите истинное направление ветра.

1.88. На стороне АВ треугольника ABC дана точка Р, через которую проведены прямые параллельно его медианам АМ₁ и ВМ₂ и пересекающие соответствующие стороны треугольника в точках A₁ и B₁. Докажите, что середина отрезка A₁B₁ точка Р и точка пересечения медиан данного треугольника лежат на одной прямой.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»

Даны векторы А = (-2; 3; 5) и B = (4; -1; 7). Найти координаты вектора

При умножении вектора на число все его координаты

Умножаются на это число, при сложении векторов складываются их соответствующие координаты.

Координаты коллинеарных векторов пропорциональны.

Если A || B, то . Отсюда:

Ответ: .

Найти направляющие косинусы вектора А = .

Направляющие косинусы являются координатами орта (единичного вектора) данного направления.

Найдем модуль вектора А:

Разделив все координаты вектора А на его модуль, получим координаты орта:

Ответ:

Тогда AA + BB + GC = <2A + B— 3G; —A + B+ G; 3A — B+ 2G>, причем координаты этого вектора должны равняться соответствующим координатам вектора D. Приравнивая эти координаты, получаем систему уравнений для определения A, B, G:

Для векторов A = , B = , C = , D = найти такие числа A, B, G, чтобы векторы AA, BB, GC и D образовали замкнутую ломаную линию, если начало каждого последующего вектора совместить с концом предыдущего.

C = линейно зависимой или линейно независимой.

Система векторов называется линейно независимой, если равенство

Вычислим главный определитель Δ системы уравнений

По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).

Поскольку других решений нет, данная система векторов линейно независима.

Ответ: Система векторов линейно независима.

Найти координаты какого-либо вектора, направленного по биссектрисе угла между векторами А = (-4; 3; 0) и B = (12; -15; 16).

Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.

Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.

Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.

При каких значениях X, Y, Z точки А(Х; -1; 3), В(5; -4; Z), C(-2; Y; 9), D(-5; 1; 7) являются вершинами параллелограмма?

Для выполнения условия задачи требуется коллинеарность векторов и и и .