Плоскость общего положения заданная параллельными прямыми

Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.

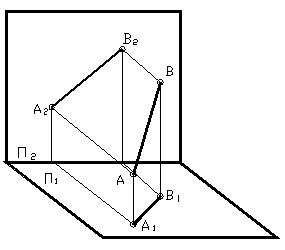
Рисунок 8

а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.

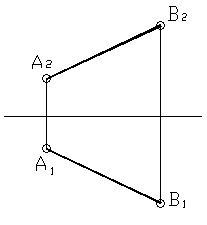
Рисунок 9

б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

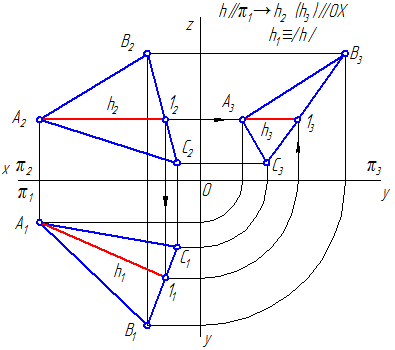
Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

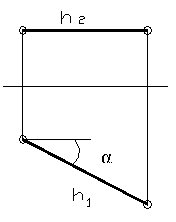
Рисунок 10

Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.

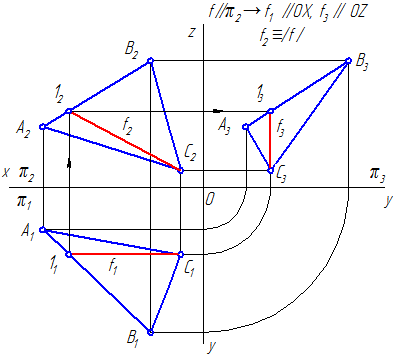
Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

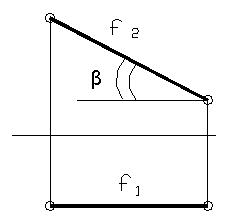
Рисунок 11

Горизонтальная проекция фронтали параллельна оси Х, а угол β — угол наклона фронтали к горизонтальной плоскости проекций; f₂ // П2, β= Ð f1 П1.

Профильная прямая – это прямая, параллельная профильной плоскости П 3 . Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β — соответственно, углы наклона прямой к плоскостям П 1 и П2.

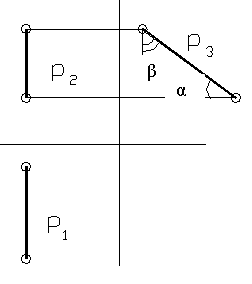
Рисунок 12.

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).

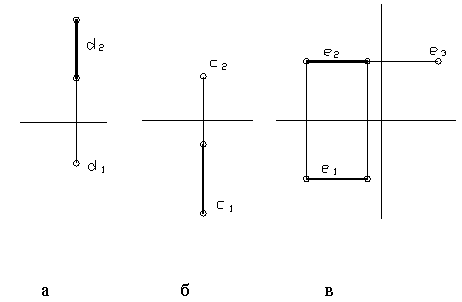
Рисунок 13

Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

а) три точки, не лежащие на одной прямой;

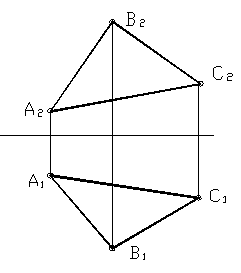
Рисунок 14

б) прямая и точка, не лежащая на ней;

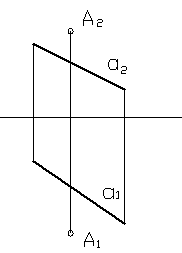
Рисунок 15

в) две параллельные прямые;

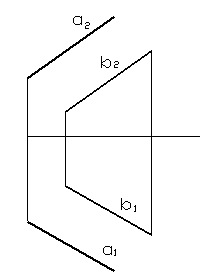
Рисунок 16

г) две пересекающиеся прямые;

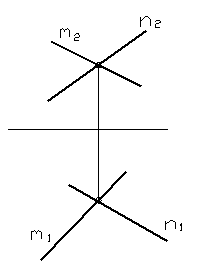
Рисунок 17

д) плоская фигура (многоугольник, круг и т.д.).

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

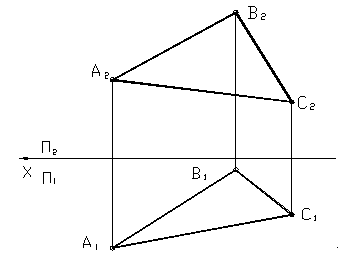
Рисунок 18

Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.

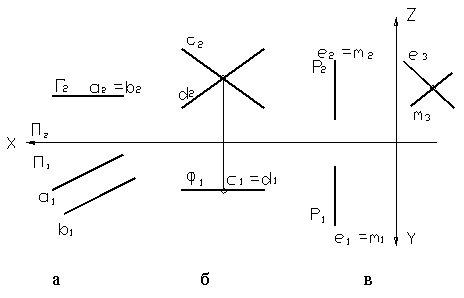
Рисунок 19

На рисунке 20 (а, б, в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) — параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.

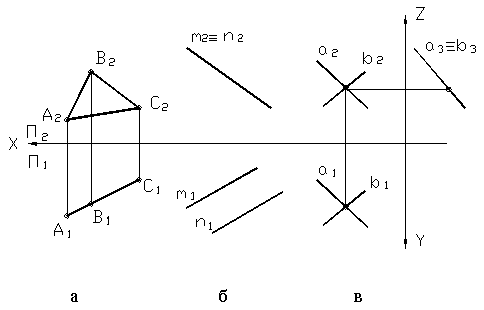
Рисунок 20

1. Как образуется комплексный чертеж прямой линии?

2. Прямые какого положения вы знаете?

3. Назовите прямые уровня.

4. Как называется прямая, проекцией которой на горизонтальной плоскости будет точка?

5. Перечислите способы задания плоскости.

6. Дайте определение плоскости общего положения.

7. Какие бывают плоскости частного положения? Как они называются и как выглядят на комплексном чертеже?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Видео:Точка встречи прямой с плоскостьюСкачать

Лекция 3. Плоскость

Видео:Проецирование плоскости общего положенияСкачать

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

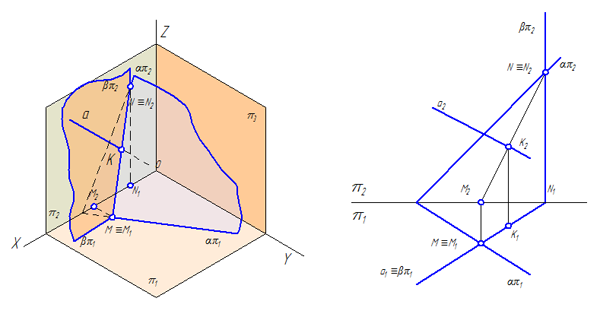
Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

Видео:Параллельность прямой к плоскостиСкачать

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

Видео:Строим фронталь и горизонталь в плоскости общего положения удаленную от П1 П2 на какое то расстояниеСкачать

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

left.beginalpha=mparallel n,\Dinalpha\Cinalpha\endright> Longrightarrow CDinalpha

Видео:Проецирование прямой общего положенияСкачать

Упражнение

Рисунок 3.7 – Решение задачи

Решение :

1. ABCD – плоский четырехугольник, задающий плоскость.
2. Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
3. Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A₂C₂ ∩ B₂D₂=K₂.
4. Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B₁D₁ строим К₁.
5. Через А₁К₁ проводим проекцию диагонали А₁С₁.
6. Точку С₁ получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А₁К₁.

Видео:Следы плоскости общего положения заданной фронталью и горизонталью. Начертательная геометрия легкоСкачать

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Интерактивная модель Горизонталь плоскости

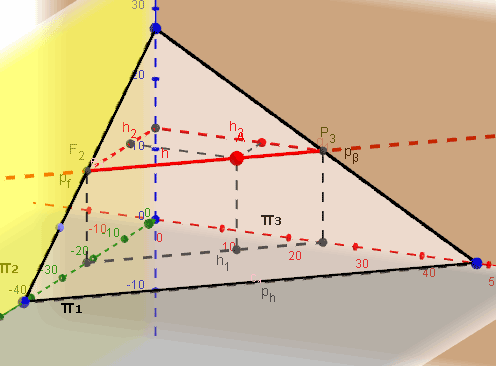Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Интерактивная модель Фронталь плоскости

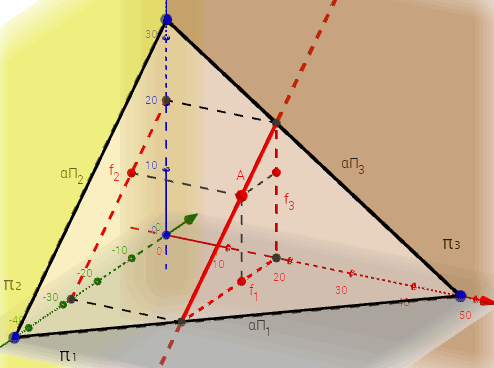Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Интерактивная модель Профильная прямая плоскости

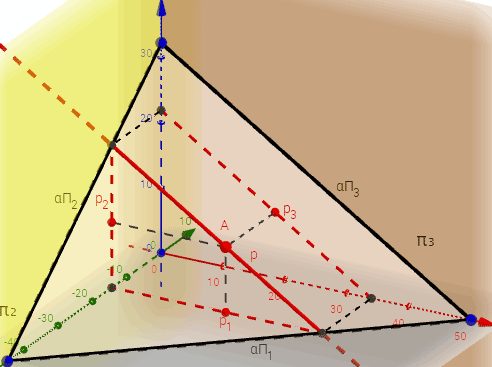Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

Видео:Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

alpha=mcap n\left.begina_2parallel m_2\a_1parallel m_1\endright> Rightarrow aparallelalpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

1. Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
2. Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
3. Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Видео:Пересечение плоскостей, заданных параллельными и пересекающимися прямымиСкачать

Упражнение

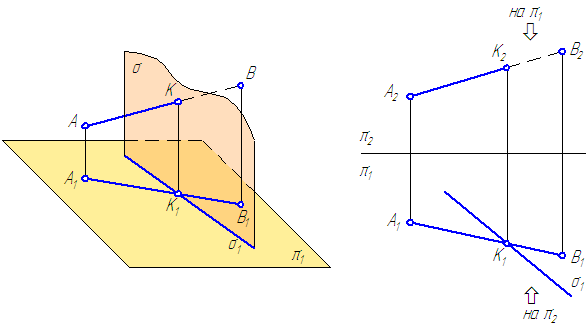
Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Решение :

1. 1. Точка К должна принадлежать прямой АВ ⇒ К₁∈А₁В и заданной плоскости σ ⇒ К₁∈σ, следовательно, К₁ находится в точке пересечения проекций А₁В₁ и σ₁;
   2. Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ₁ (горизонтальный след плоскости);
   3. Фронтальную проекцию точки К находим посредством линии проекционной связи: К₂∈А₂В₂.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Видео:Построение следов плоскостиСкачать

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

Решение:

1. Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
2. Если α⊥π₁, то на плоскость проекций π₁ плоскость α проецируется в прямую (горизонтальный след плоскости απ₁ или α₁), совпадающую с E₁F₁;
3. Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
4. Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.

Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:

1. left.beginalpha perp pi_1\alphain EF\endright> Longrightarrow alpha_1in E_1F_1
2. alphacapsigma=(1-2)left.begin|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\endright.
3. (1_2-2_2)cap E_2F_2=K_2\left.beginKin EF\Kin (1-2)Rightarrow Kinsigma\endright>Longrightarrow K=EFcap (sigma =triangle ABC)

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

Решение : В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.

1. Через точку F проводим прямую m, параллельную, например, АВ.
2. Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
3. β = m∩n и β//α по определению.

Интерактивная модель Параллельность двух плоскостей

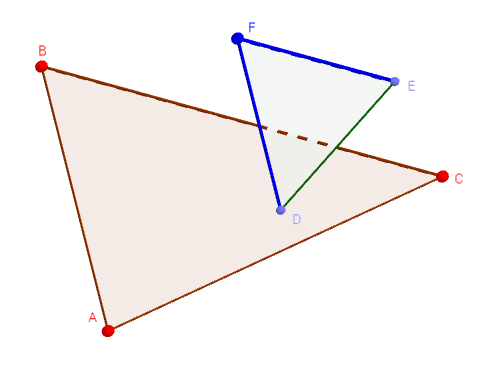3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Видео:Следы прямой Взаимное положение двух прямыхСкачать

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Порядок построения линии пересечения плоскостей:

1. Найти точку пересечения горизонтальных следов — это точка М (её проекции М₁ и М₂, при этом М₁=М, т.к. М – точка частного положения, принадлежащая плоскости π₁).
2. Найти точку пересечения фронтальных следов — это точка N (её проекции N₁ и N₂, при этом N₂=N, т.к. N – точка частного положения, принадлежащая плоскости π₂).
3. Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М₁N₁ и М₂N₂.

МN – линия пересечения плоскостей.

Видео:Лекция 1. Классификация прямых линий.Скачать

Упражнение

Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K₁ и L₁ , на пересечении горизонтального следа (α₁) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А₁В₁ и A₁C₁. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K₂ и L₂ на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K₁ и L₁; K₂ и L₂. Линия пересечения заданных плоскостей построена.

Алгоритм решения задачи :

left.beginABcapsigma=K\ACcapsigma=L\endright> left.beginRightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\endright.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Видео:Метод замены плоскостей. Нахождение расстояния между прямыми общего положенияСкачать

Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

left.beginalphacapsigma=(4-5)\betacapsigma=(3-2)\endright>\left.beginalphacaptau=(6-7)\betacaptau=(1-8)\endright>left.begin(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\endright>rightarrow\left.beginM_1N_1\M_2N_2\endright>Rightarrowalphacapbeta=MN

Видео:Взаимное пересечение двух плоскостейСкачать

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

Видео:Пересечение прямой с плоскостью общего положения. Определение видимости методом конкурирующих точекСкачать

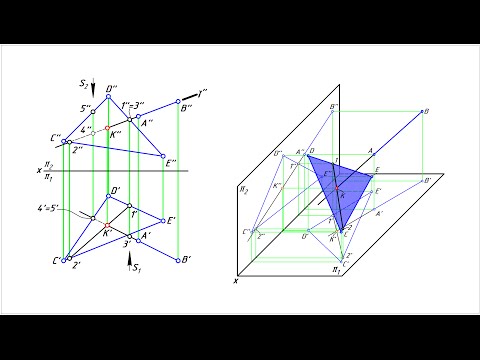
3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Комплексный чертёж плоскости. Взаимное положение плоскостей

Федеральное агентство по образованию

Государственное образовательное учреждение

«Алтайский государственный технический университет им. »

Бийский технологический институт (филиал)

КОМПЛЕКСНЫЙ ЧЕРТЁЖ ПЛОСКОСТИ.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Методические указания по изучению курса начертательной
геометрии для студентов специальностей 120100 всех форм обучения

, Левин чертёж плоскости.

Взаимное положение плоскостей: Методические указания по изучению курса начертательной геометрии для студентов специальностей 120100 всех форм обучения.

Алт. гос. техн. ун-т, БТИ. – Бийск.

Изд-во Алт. гос. техн. ун-та, 2005. – 28.

В методических указаниях представлен теоретический материал для изучения темы «Комплексный чертёж плоскости, взаимное положение плоскостей». Методические указания предназначены для самостоятельного изучения начертательной геометрии студентами специальностей 120100 дневной, вечерней
и заочной форм обучения.

Рассмотрены и одобрены

на заседании кафедры

Протокол №17 от 16.г.

доцент кафедры технической механики БТИ,

© БТИ АлтГТУ, 2005

1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ

На эпюре плоскость может быть задана проекциями геометрических элементов, определяющих ее (рисунок 1): проекциями трех точек (А, В, С), не лежащих на одной прямой; проекциями прямой (EF)
и точки (D) вне её; двумя пересекающимися прямыми (m, n); двумя параллельными прямыми (k, l).

Кроме этого, плоскость может быть задана проек­циями любой плоской фигуры — треугольника, квадрата, круга и т. д.

Из рисунка 1 нетрудно видеть, что от одной формы задания плоскости путем несложных построений можно перейти к любой другой форме. Так, соединив точки А и В прямой линией, перейдем от способа задания плоскости проекциями трех точек к способу задания плоскости проекциями прямой и точки вне ее и т. д.

1.2 Следы плоскости

На рисунке 2 изображена некоторая плоскость Р в системе V, Н, W. Эта плоскость пересекает плоскости проекций по прямым, обозначенным на чертеже Pv, PH и Pw.

Прямые, по которым некоторая плоскость Р пересе­кает плоскости проекций, называются следами этой плос­кости :

Pv — фронтальный след плоскости Р;

PH — горизонтальный след плоскости Р ;

Pw — профильный след плоскости Р.

Точки Рх, Pу, Pz — точки пересечения следов плос­кости (точки схода следов), лежащие на соответствующих осях.

На рисунке 3 дан эпюр плоскости Р в системе V, H,W.

Следовательно, плоскость на эпюре может быть задана проекциями ее следов.

На рисунке 4 дан эпюр плоскости Р, заданной проекциями ее следов, в системе V/H.

Следует иметь в виду, что фронтальная проекция фронтального следа плоскости совпадает с самим следом, а горизонтальная проекция его — с осью X. Аналогично, горизонтальная проекция горизонтального следа совпадает с самим следом, а фронтальная проекция горизонтального следа — с осью X.

Рисунок 3 Рисунок 4

2 ПРЯМАЯ В ПЛОСКОСТИ

Из элементарной геометрии известно, что прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости, или проходит через точку, принадлежащую данной плоскости, и параллельна какой-либо прямой, находящейся в этой плоскости или ей параллельной.

Рисунок 5 Рисунок 6

2.1 Построение следов плоскости

От любого из перечисленных выше способов задания плоскости можно перейти к заданию её следами, т. е. построить следы заданной плоскости.

Рисунок 7 Рисунок 8

На рисунках 7 и 8 построены следы плоскостей, заданных двумя параллельными и двумя пересекающимися прямыми. Построения в обоих случаях аналогичны: вначале построены следы прямых и через одноименные следы прямых проведены следы плоскости (так как следы прямых, принадлежащих плоскости, всегда находятся на одноименных следах плоскости).

2.2 Прямые особого положения в плоскости

К прямым особого положения в плоскости относятся следующие.

Горизонтали плоскости.─ это прямые, лежащие в данной плоскости и параллельные плоскости проекций Н.

Горизонтальная проекция горизонтали всегда параллельна горизонтальному следу плоскости, а фронтальная ─ параллельна оси X.

На рисунке 9 изображена горизонталь MN плоскости, заданной двумя пересекающимися прямыми Е и F .

Фронтали плоскости ─ это прямые, лежащие в данной плоскости и параллельные плоскости проекций V.

Фронтальная проекция фронтали всегда параллельна фронтальному следу плоскости, а горизонтальная ─ параллельна оси X (рису-
нок 10).

Рисунок 9 Рисунок 10

На рисунке 11 изображена фронталь AD плоскости, заданной треугольником ABC, проходящая через точку А.

Рисунок 11 Рисунок 12

Линии наибольшего ската плоскости относительно плоскости Н ─ это прямые, лежащие в заданной плоскости и перпендикулярные к горизонталям этой плоскости, в том числе и к её горизонтальному следу (рисунок 12).

ВК ─ линия наибольшего ската плоскости Q. BК ^ QH, но и bk^ QH (на основании теоремы о проекциях прямого угла). Значит, угол ВКb— линейный угол двугранного угла, образованного плоскостями Q и Н. Следовательно, линия наибольшего ската плоскости может служить для определения угла наклона этой плоскости к плоскости проекций Н.

На рисунках 13 и 14 приведено построение линии наибольшего ската ВК в плоскостях, заданных следами (рисунок 13) и треугольником ABC (рисунок 14).

3 ХАРАКТЕРНЫЕ ПОЛОЖЕНИЯ ПЛОСКОСТИ
ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ

По положению плоскостей относительно плоскостей проекций различают:

1. Плоскости, не перпендикулярные ни к одной из плоскостей проекций. Это плоскости общего положения (рисунок 15). Следы плоскостей общего положения никогда не перпендикулярны к осям проекций.

2. Плоскости, перпендикулярные к одной из плоскостей проекций:

а) плоскости, перпендикулярные к горизонтальной плоскости проекций ─ это горизонтально проектирующие плоскости (рисунок 16),

у которых фронтальный след всегда перпендикулярен к оси X. Если
в горизонтально проектирующей плоскости находится точка или прямая, то их горизонтальные проекции всегда будут находиться на горизонтальном следе плоскости. Угол b (рисунок 16) равен углу между горизонтально проектирующей плоскостью и плоскостью проекций V;

б) плоскости, перпендикулярные к фронтальной плоскости проекций — это фронтально проектирующие плоскости (рисунок 17), у которых горизонтальный след всегда перпендикулярен к оси X. Если во фронтально проектирующей плоскости находится точка или прямая, то их фронтальные проекции всегда лежат на фронтальном следе плоскости. Угол a (рисунок 17)—угол между фронтально проектирующей плоскостью
и плоскостью проекций Н;

в) плоскости, перпендикулярные к профильной плоскости проекций, ─ это профильно проектирующие плоскости (рисунок 18).

Рисунок 19 Рисунок 20

3. Плоскости, перпендикулярные к двум плоскостям проекций:

а) плоскости, перпендикулярные к плоскостям V и W , т. е. параллельные плоскости Н, ─ это горизонтальные плоскости (рисунок 21);

б) плоскости, перпендикулярные к плоскостям Н и W, т. е. параллельные плоскости V, ─ это фронтальные плоскости (рисунок 22);

в) плоскости, перпендикулярные к плоскостям Н и V, т. е. параллельные плоскости W, ─ это профильные плоскости (рисунок 23).

4 ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ

Две плоскости могут быть параллельны или пересекаться.

Из элементарной геометрии известно, что две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Иными словами, если плоскости параллельны, то всегда в каждой из них можно построить по две пересекающиеся прямые так, чтобы прямые одной плоскости были соответственно параллельны двум прямым другой плоскости (рисунок 24). Все три плоскости (см. рисунок 24) параллельны между собой.

Но такими пересекающимися прямыми могут быть и следы плоскости. Следовательно, если два пересекающихся между собой следа одной плоскости параллельны одноименным следам другой плоскости, то обе плоскости параллельны между собой (рисунок 25).

Если хотя бы одна пара одноименных следов двух плоскостей пересекается, то плоскости пересекаются (рисунок 26).

Если же плоскости заданы не пересекающимися, а параллельными следами (рисунок 27), то для решения вопроса, пересекаются они или параллельны, надо построить их следы на третьей плоскости проекций (рисунок 28).

Изображенные на рисунке 28 плоскости Р и Q пересекаются,
а плоскости R и S параллельны.

4.1 Построение взаимно параллельных плоскостей

На рисунке 29 через точку К проведена плоскость, параллельная плоскости, заданной двумя пересекающимися прямыми АВ и ВС. Искомая плоскость также выражена двумя пересекающимися прямыми, соответственно параллельными заданным.

На рисунке 30 через точку С проведена плоскость, параллельная плоскости, заданной двумя параллельными прямыми Е и F. Искомая плоскость выражена двумя пересекающимися прямыми, одна из которых проведена параллельно прямым, определяющим заданную плоскость, а вторая — параллельно произвольной прямой 1—2, взятой в заданной плоскости.

На рисунке 31 через точку А проведена плоскость Q, параллельная плоскости Р, заданной следами. Для этого через точку А проведена вначале горизонталь AN искомой плоскости (горизонтальная проекция горизонтали искомой плоскости должна быть параллельна Рн), определен фронтальный след (N) этой горизонтали и через фронтальную проекцию (п’) следа проведен фронтальный след (Qv) искомой плоскости. Горизонтальный след (Qn) плоскости проведен из тачки Qx параллельно Рн (или параллельно горизонтальной проекции горизонтали AN).

4.3 Линия пересечения двух плоскостей

Линия пересечения двух плоскостей — это прямая, принадлежащая как одной, так и другой плоскости. Но положение любой прямой
в пространстве определяется положением двух ее точек. Следовательно, для построения линии пересечения двух плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям.

Если плоскости заданы следами, то эти точки находят в точках пересечения одноименных следов плоскостей. Линия, проходящая через эти точки, и будет линией пересечения плоскостей.

На рисунках 33—38 приведены примеры построения линии пересечения двух плоскостей, заданных следами.

В тех случаях, когда одна или обе плоскости заданы не следами, для построения линии их пересечения обычно применяют способ дополнительных секущих плоскостей.

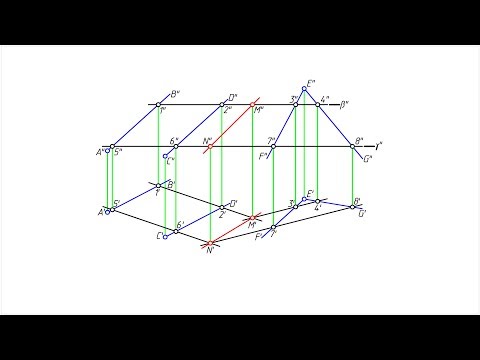
На рисунке 39 плоскости заданы двумя пересекающимися прямыми АВ и ВС и двумя параллельными прямыми d и е. Для нахождения линии их пересечения проведена вспомогательная горизонтальная плоскость Т1. Эта плоскость пересекла плоскость, заданную пересекающимися прямыми, по прямой /—2, а плоскость, заданную параллельными прямыми, по прямой 3—4. Точка пересечения этих прямых — точка К1 является общей для обеих заданных плоскостей, т. е. одной из точек линии пересечения. Вторая точка К2 найдена аналогично при помощи вспомогательной горизонтальной плоскости Т2. Линия, проходящая через точки К1 и К2, является искомой линией пересечения двух плоскостей.

Способ построения линии пересечения двух плоскостей при помощи дополнительных секущих плоскостей применим также и в тех
случаях, когда обе плоскости заданы следами. На рисунке 40 одна точка линии пересечения плоскостей Т и R (точка М) найдена в точке пересечения горизонтальных следов плоскостей, а вторая точка (точка К) — при помощи дополнительной секущей горизонтальной плоскости S.

В тех случаях, когда одна из заданных пересекающихся плоскостей является плоскостью частного положения, построение линии пересечения их значительно упрощается. На рисунке 41 одна из заданных плоскостей (плоскость треугольника DEF) является горизонтально проектирующей. Построение линии пересечения этих плоскостей свелось к построению фронтальных проекций точек 1 и 2, принадлежащих искомой линии.

Вопросы для самопроверки

1. Покажите способы задания плоскости общего положения и проецирующих плоскостей.

2. Как строят прямые линии и точки в плоскости?

3. Изложите особенности проецирующих плоскостей.

4. Покажите способы построения горизонтали, фронтали и линии наибольшего наклона плоскостей общего положения и проецирующих плоскостей.

5. Какое положение могут занимать плоскости относительно друг друга?

6. Признак параллельности двух плоскостей.

7. Как построить линию, общую для двух пересекающихся плоскостей?

1. Гордон, В. О. Курс начертательной геометрии / , -Огиевский; под ред. . – 25-е изд., стер. – М.: Высш. шк., 2003.

2. Гордон, В. О. Сборник задач по курсу начертательной геометрии / , , ; под ред. . – 9-е изд., стер. – М.: Высш. шк., 2003.

3. Курс начертательной геометрии / под ред. . – 24-е изд, стер. – М.: Выcшая школа, 2002.

4. Начертательная геометрия / под ред. . – 7-е изд., перераб. и доп. – М.: Выcшая школа, 2000.

5. Начертательная геометрия. Инженерная и машинная графика: программа, контрольные задания и методические указания для студентов-заочников инженерно-технических и педагогических специальностей вузов / , , ; под ред. . – 2-е изд., испр. – М.: Выcшая школа, 2001.

6. Фролов, геометрия / . – М.: Машиностроение, 1978.

7. Бубенников, геометрия / , . – М.: Высшая школа, 1973.

8. Начертательная геометрия / под общей ред. . – Минск: Вышейшая школа, 1967.

9. Боголюбов, : учебник для машиностроительных специальностей средних специальных учебных заведений / . – 3-е изд., испр. и дополн. – М.: Машиностроение, 2000.

1 Способы задания плоскости…………………………………………….3

2.1 Построение следов плоскости…………………………………..5

2.2 Прямые особого положения в плоскости………………………6

3 Характерные положения плоскости относительно плоскостей

4 Взаимное положение двух плоскостей………………………………..13

4.1 Построение взаимно параллельных плоскостей……………..16

4.3 Линия пересечения двух плоскостей……………………….…18

Вопросы для самопроверки………………………………………….…..25

Комплексный чертёж плоскости.

Взаимное положение плоскостей

Методические указания по изучению курса начертательной геометрии для студентов специальностей 120100 всех форм обучения

Подписано в печать 25.10.04. Формат 60х84 1/16.

Усл. п. л. 1,63 Уч.-изд. л. 1,75

Печать – ризография, множительно-копировальный

аппарат «RISO TR -1510»

Тираж 60 экз. Заказ 2005-03.

Издательство Алтайского государственного

Оригинал-макет подготовлен ИИЦ БТИ АлтГТУ.

Отпечатано в ИИЦ БТИ АлтГТУ.

КОМПЛЕКСНЫЙ ЧЕРТЁЖ ПЛОСКОСТИ.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Методические указания по изучению курса начертательной
геометрии для студентов специальностей 120100 всех форм обучения