- Отношение и пропорциональность отрезков
- Работа моих учеников. Презентация «Исторические факты о подобии треугольников» (8 класс)
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Описание презентации по отдельным слайдам:
- Подобные треугольники
- Скачать:
- Предварительный просмотр:
- 📸 Видео
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Отношение и пропорциональность отрезков
Идея отношения и Пропорции зародилась в глубокой древности. Об этом свидетельствуют древнеегипетские храмы, детали гробницы Менеса и знаменитых пирамид в Гизе (III тысячелетие до н. э.), вавилонские зиккураты (ступенчатые культовые башни), персидские Дворцы, Индийские и другие Памятники древности, Многие обстоятельства. В том числе особенности архитектуры, требования Удобства, Эстетики, техники и экономичности при возведении зданий и сооружений, вызвали возникновение и развитие понятий отношения и пропорциональности отрезков, площадей и других величин.
В «Московском» папирусе при рассмотрении, отношения большего катета к меньшему в одной из задач на прямоугольный треугольник применяется специальный знак для понятия «отношение».
В «Началах» Евклида учение об отношениях излагается дважды, В VII книге содержится арифметическая теория. Она относится только к соизмеримым величинам и к целым числам. Эта теория создана на основе практики действия с дробями. Евклид применяет ее для исследования свойств целых чисел. В V книге излагается общая теория отношений и пропорций, разработанная Евдоксом. Она лежит в основе учения о подобии фигур, изложенного в VI книге «Начал».
Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Работа моих учеников. Презентация «Исторические факты о подобии треугольников» (8 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Работа ученика 8 «б» класса МБОУ СОШ № 50 г. Новосибирска Грецких Константина
Уже в XVI в. нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.
Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей. Немного из истории Вот один пример из «Устава ратных, пушечных и других дел, касающихся до военной науки»:
За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени. ПРИТЧА:
« Усталый чужеземец пришёл в страну Великого Хапи. Солнце уже садилось, когда он подошёл к великолепному дворцу фараона. Он что-то сказал слугам. По мановению руки распахнулись перед ним двери и провели его в приёмную залу. И вот он стоит в запылённом походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители великих тайн природы. — Кто ты? – спросил верховный жрец. — Зовут меня Фалес. Родом я из Милета. Жрец надменно продолжал: — Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на неё? – Жрецы согнулись от хохота. — Будет хорошо, — насмешливо продолжал жрец, — если ты ошибёшься не более чем на 100 локтей. — Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра. Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они – жрецы великого Египта. — Хорошо, — сказал фараон. – Около дворца стоит пирамида, мы знаем её высоту. Завтра проверим твоё искусство».
На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.
Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида. СЕ=ED, т.е. H=b Преимущества: не требуются вычисления. Недостатки: нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.
«Таинственный остров» (фр. L’Île mystérieuse) — роман-робинзонада французского писателя впервые опубликованный в 1874 году. Является продолжением известных произведений Верна «20000 лье под водой» и «Дети капитана Гранта». В книге повествуется о событиях, происходящих на вымышленном острове, где остановился капитан Немо на своей подводной лодке «Наутилус». Основными персонажами являются пятеро американцев, которые оказываются на необитаемом острове в Южном полушарии.
Нахождения четвертого неизвестного члена пропорции. Преимущества: можно производить измерения в любую погоду; простота формулы. Недостатки: нельзя измерить высоту предмета не испачкавшись, так как приходится ложиться на землю.
АВD подобен EFD (по двум углам): ВАD= FED=90°; АDВ = EDF, т.к. угол падения равен углу отражения. В подобных треугольниках сходственные стороны пропорциональны: ; . ; . ; .
Преимущества: можно производить измерения в любую погоду; одежда будет чистой; простота формулы; Недостатки: нужно специальное приспособление: зеркало.
По построению АВС подобен А1В1С1 (по двум углам). В подобных треугольниках сходственные стороны пропорциональны: А В С А1 В1 С1
Нахождение ширины озера Длина тени земного шара
Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Подобные треугольники
Представленная работа посвящена подобию треугольников. В работе показано:
— применение дополнительных построений: использование в решении задач «выносного» чертежа, то есть фрагмента, имеющегося достаточно сложного чертежа, вынесенного отдельно для специального изучения;
— необходимость выработки умений и навыков по решению практических задач, так как, столкнувшись с реальными подобными ситуациями, они будут нужны в жизни;
— быстрота и красота решений.
И что еще немало важно – эти задачи связывают несколько дисциплин – алгебру, геометрию и физику и показывают насколько целостный и взаимосвязанный мир наук.
Видео:Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать

Скачать:
| Вложение | Размер |
|---|---|
| Подобные треугольники | 648 КБ |
| Презентация | 1.84 МБ |
Видео:Подобные треугольникиСкачать

Предварительный просмотр:
Краевой конкурс научных проектов школьников в рамках краевой научно-практической конференции «Эврика» Малой академии наук учащихся Кубани
Секция: «Математика, компьютерные технологии»
Михайленко Яна Юрьевна
Россия, Краснодарский край
Каневской район, ст. Каневская
МБОУ СОШ №6, 10 класс
Михайленко Любовь Александровна,
учитель математики и физики
ст. Каневская 2012 год
Михайленко Яна Юрьевна
Россия, Краснодарский край, Каневской район,
станица Каневская МБОУ СОШ №6,10 класс
Научный руководитель: Михайленко Любовь Александровна,
учитель математики и физики МБОУ СОШ №6
Представленная работа посвящена подобию треугольников.
Актуальность настоящей работы обусловлена тем, что зная, признаки подобия можно научиться рационально решать задачи, как по математике, так и по физике.
Цель исследования: выявить геометрические теоремы, свойства и показать их применение в решениях задач, связанных с треугольниками.
В работе использован поисково-исследовательский метод, способствующий нахождению более простых решений предложенных заданий.
В работе показано:
— применение дополнительных построений: использование в решении задач «выносного» чертежа, то есть фрагмента, имеющегося достаточно сложного чертежа, вынесенного отдельно для специального изучения;
— необходимость выработки умений и навыков по решению практических задач, так как, столкнувшись с реальными подобными ситуациями, они будут нужны в жизни;
— быстрота и красота решений.
И что еще немало важно – эти задачи связывают несколько дисциплин – алгебру, геометрию и физику и показывают насколько целостный и взаимосвязанный мир наук.
1.Из истории подобия……………………………………………….5 стр
2.Подобные треугольники………………. 6 стр
3.Применение подобия при доказательстве теорем и задач……..7 стр
4.Применение подобия при решении задач по математике…….11 стр
5.Применение подобия при решении задач по физике………….14 стр
СПИСОК ЛИТЕРАТУРЫ……………………………………….. 20 стр
Михайленко Яна Юрьевна
Россия, Краснодарский край, Каневской район,
станица Каневская МБОУ СОШ №6,10 класс
Научный руководитель: Михайленко Любовь Александровна,
учитель математики и физики МБОУ СОШ №6
Геометрия – это не просто наука о свойствах треугольников, параллелограммов, окружностей. Геометрия – это целый мир, который окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.
Треугольник – самая простая геометрическая фигура, знакомая нам с детства. К треугольнику на уроках геометрии мы обращаемся чаще всего. Эта фигура таит в себе немало интересного и загадочного, как Бермудский треугольник, в котором бесследно исчезают корабли и самолеты. Один мудрец сказал: “Высшее проявление духа – это разум. Высшее проявление ума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная”.
Изучая геометрию, я поняла, что тема «Подобные треугольники» является одной из самых актуальных, обширных и распространенных в математике. Много теорем, следствий рассматривает этот раздел. Умение решать задачи на применение признаков подобия широко используется в геометрии, физике, астрономии.
Поэтому цель моей работы – выявить теоремы и показать их применение и рациональное использование в решении задач.
Идея отношения и пропорции зародилась в глубокой древности. Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров. Особенности архитектуры, требования удобства, эстетики, техники и экономичности при возведении зданий и сооружений, вызвали возникновение и развитие понятий отношения и пропорциональности отрезков, площадей и других величин. До наших дней сохранилась клинописная табличка, в которой речь идет о построении пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов.
Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V—IV вв. до н. э. трудами Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге «Начал» Евклида, начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».
Греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и фараон, собравшиеся у подножия высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывавшего высоту огромного сооружения.
Фалес,– говорит предание,– избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна так же равняться длине отбрасываемой ею тени. Конечно, длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить непосредственно. Изменим, этот способ так, чтобы в солнечный день можно было воспользоваться любой тенью, какой бы длины она ни была. Пусть длина шеста 1м, а его тени 1,2м. Найти высоту дерева, если ее тень 6м.
Таких красивых задач, которые решаются с применением признаков подобия, очень много.
Два треугольника называют подобными, если их углы соответственно равны, и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Признаки подобия треугольников
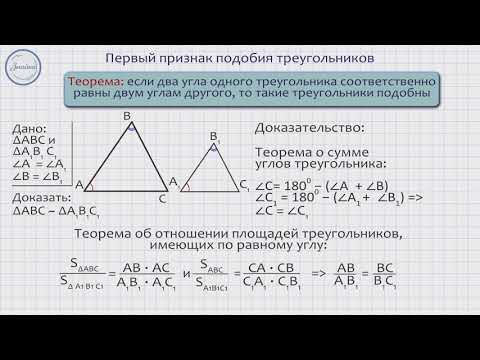
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
3) Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Теорема о площадях двух подобных треугольников
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
- Применение подобия при доказательстве теорем и задач [1]
Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство. Пусть MN– средняя линия треугольника ABC. Докажем, что MN//AC и MN = ½ АС
Треугольники BMN и ВАС подобны по второму признаку подобия треугольников (угол B – общий) ВМ/ВА = BN/BC = ½ ), поэтому углы 1 и 2 равны и MN/AC = ½ . из равенства углов 1 и 2 следует, что MN//AC, а из второго равенства, что MN = ½ АС
Задача. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Решение. Рассмотрим произвольный треугольник ABC. Обозначим буквой О точку пересечения его медиан AA 1 и BB 1 и проведём среднюю линию A 1 B 1 ,этого треугольника. Отрезок A 1 B 1 параллелен стороне АВ, поэтому углы 1 и 2, 3 и 4 равны. Следовательно,
треугольники АОВ u A 1 OB 1 подобны по двум углам, и, значит, их стороны пропорциональны: AO/A 1 O = BO/B 1 O = AB/A 1 B 1 . Но АВ = 2А 1 В 1 , поэтому АО = 2A 1 O и ВО = 2B 1 O. Таким образом, точка О пересечения медиан AA 1 и BB 1 делит каждую из них в отношении 2:1, считая от вершины.
Аналогично доказывается, что точка пересечения медиан BB 1 и СС 1 делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О. Итак, все три медианы треугольника ABC пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.
Следующие утверждения также доказываются с помощью подобия
1 0 Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
2 0 Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.
3 0 Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
4 0 Если хорды АВ и CD окружности пересекаются в точке S, то AS ∙BS = CS∙DS, то есть DS/BS = AS/CS.
5 0 Если из точки Р к окружности проведены две секущие, пересекающие окружность в точках А, В и С, D соответственно, то АР/СР = DP/BP.
6 0 Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.
7 0 Середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон трапеции лежат на одной прямой.
Теорема Чевы [ 2 ]
Пусть точки A 1 , B 1 и С 1 принадлежат сторонам BC, AC и AB треугольника ABC. Отрезки AA 1 , BB 1 и CC 1 пересекаются в одной точке тогда и только тогда, когда
Доказательство: Докажем сначала, что если отрезки пересекаются, то произведение отношений равно 1. Пусть O — точка пересечения отрезков AA 1 , BB 1 и CC 1 . Проведём через точку A прямую q, параллельную прямой BC . Продолжим отрезки BB 1 и CC 1 за точки В 1 и C 1 до пересечения с прямой q в точках В 2 и C 2 соответственно. Тогда треугольники ВОА 1 и В 2 0А подобны по двум углам. Также подобны треугольники COA 1 и C 2 OA. Следовательно, . Также подобны треугольники BB 1 C и B 2 B 1 A, а значит, . Аналогично . Перемножив три получившихся равенства, получим:
Докажем обратное утверждение. Пусть отрезки AA 1 и BB 1 пересекаются в точке O. Проведем через точки C и O прямую. Пусть эта прямая пересекает сторону AB в точке K. В этом случае точки A 1 , B 1 и K удовлетворяет данному соотношению по выше доказанному. Но точки A 1 , B 1 и C 1 также удовлетворяют данному соотношению. Значит, точки K и C 1 делят сторону AB в равном соотношении, то есть они совпадают. Но CK проходит через точку O. Следовательно, отрезок CC 1 также проходит через эту точку. Значит, отрезки AA 1 , BB 1 и CC 1 пересекаются в точке O. Что и требовалось доказать.
- Применение подобия при решении задач по математике
1. Внутри треугольника ABC взята точка М, через которую проведена прямая, параллельная сторонам треугольника. При этом площади трёх образовавшихся треугольников с вершиной М равны S 1, S 2 , S 3 . Найдите площадь треугольника ABC.
Решение. Т. к. ΔАВ С
ΔА 1 А 2 М, ΔАВС
Δ С 2 МС 1 , то их площади относятся как квадраты соответствующих элементов, а именно: . Тогда . Отсюда .
2. В трапеции MNPK (MK и NP — основания) О — точка пересечения диагоналей. Площади Δ MOK и Δ NOP равны S 1 и S 2 соответственно. Найдите площадь трапеции.
Решение. Проведём OO 1┴ NР, OO 2┴ MK, тогда O€O 1 O 2 , и O 1 O 2┴ NP, O 1 O 2┴ MK. ΔMOK
ΔPON по двум углам, отсюда , т.е. ;
Ответ:
3. Расстояния от точки пересечения диагоналей равнобокой трапеции до середин её сторон равны 2 см, 1 см и 2 см соответственно. Найдите радиус окружности, описанной около трапеции.
Решение. Радиус окружности, описанной около трапеции, найдём как радиус окружности, описанной около ΔACD. Точки F, N, М — середины отрезков ВС, CD, AD соответственно. Тогда по условию, FO=1, ON=OM=2. Треугольники ВОС и AOD подобны, а потому, АO=2OС. Построим DK // ON, тогда АК .= КО = ОС и KD = 4. KD — медиана ΔAOD, ОМ — серединный перпендикуляр к AD и медиана ΔAOD. Точка Т — точка пересечения медиан ΔAОD делит медиану DK на отрезки: 8/3 и 4/3, делит медиану ОМ на отрезки: 4/3 и 2/3.
Пусть L — середина ОК, тогда L — середина АС. ΔКТО — равнобедренный, т. к. ОТ = КТ =4/3 и TL — является серединным перпендикуляром к отрезку АС. Следовательно, точка Т является центром окружности, описанной около ΔACD, радиус которой равен 8/3.
4. На сторонах АВ и АС треугольника ABC взяты соответственно точки М и N так, что ВМ = MN = NC. Отрезки ММ 1 и NN 1 — биссектрисы треугольника AMN. Докажите, что M 1 N 1 // ВС.
Решение. Угол MNA — внешний для равнобедренного треугольника MNC, поэтому угол MNA = NMC + NCM = 2NCM. Так как NN 1 — биссектриса, то угол ANN 1 = 1/2MNA = NCM. Получим, что ΔANN 1 подобен ΔАСМ по двум углам (угол А — общий). Следовательно,
AN 1 /AN = AM/AC. (1)
Проводя аналогичные рассуждения, из подобия треугольников АММ 1 и ABN получим
Поделив равенство (1) на (2) получим AN 1 /AM 1 = АВ/АС, и так как угол А — общий для треугольников AN 1 M 1 и ABC, то они подобны. Значит, угол AN 1 M 1 =АВС. Следовательно, M 1 N 1 // СВ
5. Дан правильный тетраэдр SABC, объем которого равен V. На ребрах SA и SB взяты их середины D и E, а на ребре SC взята точка F такая, что SF:FC=1:3. Найдите объем пятигранника DEFABC.
Пусть G – середина ребра SC. Тогда F – середина отрезка SG и поэтому EF – средняя линия в треугольнике SBG. Аналогично, DF – средняя линия в треугольнике SAG и по условию DE – средняя линия в треугольнике SAB. Значит, при гомотетии с центром S и коэффициентом 2 пирамида SDEF перейдет в пирамиду SABG, то есть эти пирамиды подобны с коэффициентом 2. Следовательно, объем пирамиды SDEF в 8 раз меньше объема пирамиды SABG.
Но последний объем составляет половину всего объема V. Действительно, отрезок SG перпендикулярен отрезкам AG и BG, так как они являются высотами в соответствующих гранях. Значит, прямая SC перпендикулярна плоскости ABG, и поэтому при симметрии относительно этой плоскости пирамида SABG перейдет в пирамиду CABG. Поэтому их объемы равны, в сумме они составляют V и, значит объем каждой из них равен половине V.
В итоге, V SDEF =1/8 V SABG = 1/8*1/2 V=1/16 V и поэтому V DEFABC =15/16 V.
- Применение подобия при решении задач по физике
1. Найти высоту предмета, к основанию которого можно подойти с помощью подобия треугольников?
Берем два кола BD и CE и устанавливаем их так, чтобы точки А, В и C находились на одной прямой.
Измеряем BD и СЕ, а также DG и DE. Если провести прямую CH ║ EG, то ∆ACH
∆BCF , следовательно, , откуда ;
2. Лодочник, направляясь из пункта А в пункт В, всё время направляет лодку под углом α к берегу. Найти скорость лодки относительно воды, если скорость течения реки равна u, а лодку снесло ниже пункта В на расстояние l.
В основу решения положен факт подобия треугольников сложения скоростей и сложения перемещений.
НСО – неподвижная система отсчёта (берег), ПСО – подвижная система отсчёта (вода).
Из условия задачи следует, что АС – перемещение лодки относительно берега – . Вектор скорости направлен вдоль .
Однако величина этого вектора неизвестна. Достроим треугольник скоростей, используя закон сложения скоростей
для чего через конец вектора проведём линию, параллельную берегу, до пересечения с АС. Получившийся отрезок не что иное, как , а точка пересечения линии, вдоль которой он направлен, и АС – конец вектора . Треугольник скоростей готов.
Теперь достроим треугольник перемещений. Продлив линию, вдоль которой направлен вектор , до пересечения с противоположным берегом, получим вектор – перемещение лодки в ПСО. Вектор, соединяющий концы векторов и , есть не что иное, как вектор перемещения ПСО относительно НСО – . Треугольник перемещений готов.
Треугольники скоростей и перемещений подобны по определению.
Составим отношение подобия
После подстановки и сокращений получаем конечную формулу.
3. Фонарь весом 43 Н укреплён на подвесе. Определите силу упругости бруска
АВ и проволоки ВС [ 4 ]
Решение. Запишем условие равновесия точки В
Расставить эти силы на чертеже сразу невозможно. Не определены направления и величины действующих на точку В сил упругости и .
Преобразуем формулу (1).
Используя формулу (1.1), построим силы, начиная с . От точки В в сторону, противоположную , построим –
Разложим вектор – на направления действия сил и .
Треугольник BKL, образованный силами, подобен треугольнику АВС по построению.
Составим отношения подобия
4. Два заряда по 10 -8 Кл находятся в воздухе на расстоянии 8 м друг от друга. Найдите
напряженность на расстоянии 5 м от обоих зарядов. [4]
Решение. Как видно из рисунка, таких точек две (D и Е). Решение проводят для одной из них, например для D. Заряды в точках А и В обозначают соответственно q A и q B , Е А и Е в — модули напряженностей в точке D, созданные зарядами q A и q B . По условию задачи q A = q B . Общая напряженность электрического поля в точке D: E D = Е А + Е в , которую находят как диагональ параллелограмма со сторонами векторов напряженности Е А и Е в .
Модули напряженностей Е А = Е в = k , а модуль напряженности E D определяют
из подобия ∆ ACD и ∆ DMF: DF = DM
Подставляя числовые данные, получим E D = 4,3 Н/Кл.
Приведённые примеры показывают, что использование способа, основанного на подобии треугольников, позволяет существенно упростить и сократить решение задачи. Особенно примечательно, что он не требует знакомства с дополнительным математическим материалом и основывается на часто используемых в геометрии подходах к решению стандартных геометрических задач.
Как найти расстояние до недоступной точки? Как путём построения подобных треугольников найти расстояние между двумя недоступными пунктами А и В? Как найти высоту предмета, к основанию которого можно подойти?
Решение подобных задач способствует развитию логического мышления, умению анализировать ситуацию, а использование метода подобия треугольников в их решении, повышает тем самым математическую культуру, развивая математические способности. Использовать рассмотренный мною геометрический материал можно как на уроках геометрии и физики, так и при подготовке к Единому государственному экзамену, а также на элективных курсах математического и физического направления.
- Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7-9 классы: учебник для общеобразовательных учреждений – М.: «Просвещение», 2010
- Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 10-11 классы: учебник для общеобразовательных учреждений – М.: «Просвещение», 2010
- Дениз Сечеи. Геометрия. Шаг за шагом- М.: Аст: Астрель, 2006
- Каменецкий С.Е., Орехов В.П. Методика решения задач по физике в средней школе. — М.: «Просвещение, 1987
📸 Видео
Подобные треугольникиСкачать

Первый признак подобия треугольников. Доказательство. 8 класс.Скачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Первый признак подобия треугольниковСкачать

Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Геометрия 8 класс. Первый признак подобия треугольниковСкачать
Задача на подобие треугольников 1частьСкачать

Признаки равенства и подобия треугольниковСкачать

Второй признак подобия треугольников. Доказательство. 8 класс.Скачать

Первый признак подобия треугольников.Скачать
8 класс, 23 урок, Второй признак подобия треугольниковСкачать

Геометрия 8 класс. Третий признак подобия треугольниковСкачать

Первый признак подобия треугольников | Геометрия 7-9 класс #59 | ИнфоурокСкачать

8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать




