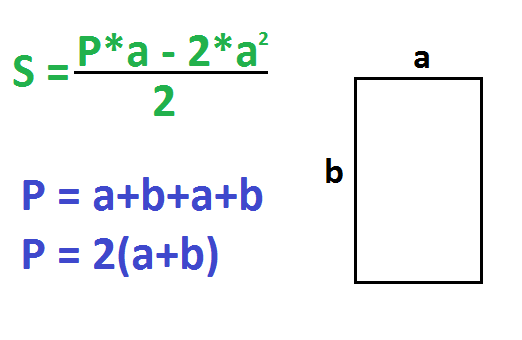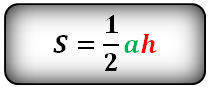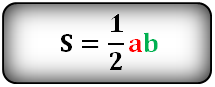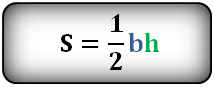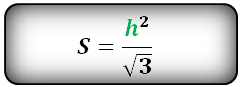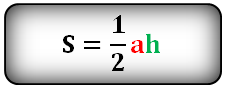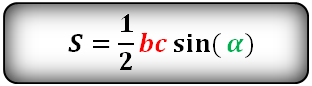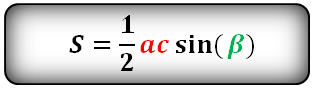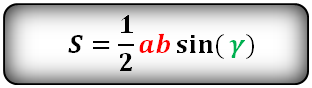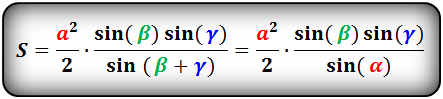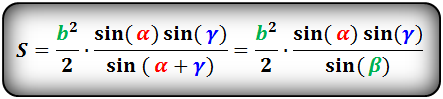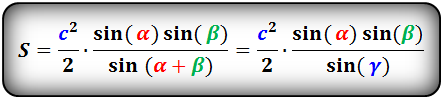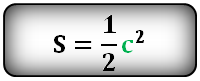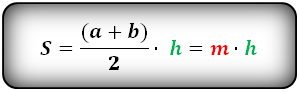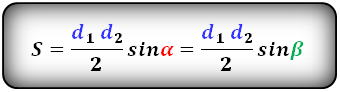Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
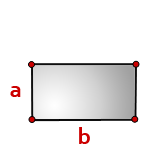
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
- По диагонали и стороне
- По стороне и диаметру описанной окружности
- По радиусу описанной окружности и стороне
- По стороне и периметру – 1 способ
- По стороне и периметру – 2 способ
- По диагонали и углу между диагоналями
- По радиусу описанной окружности и углу между диагоналями – первый способ
- По радиусу описанной окружности и углу между диагоналями – второй способ
- Площадь прямоугольника через окружность
- Как найти площадь прямоугольника – 9 способов с формулами и примерами
- По диагонали и стороне
- По стороне и диаметру описанной окружности
- По радиусу описанной окружности и стороне
- По стороне и периметру – 1 способ
- По стороне и периметру – 2 способ
- По диагонали и углу между диагоналями
- По радиусу описанной окружности и углу между диагоналями – первый способ
- По радиусу описанной окружности и углу между диагоналями – второй способ
- Прямоугольник. Онлайн калькулятор
- Свойства прямоугольника
- Диагональ прямоугольника
- Окружность, описанная около прямоугольника
- Формула радиуса окружности описанной около прямоугольника
- Периметр прямоугольника
- Формулы сторон прямоугольника через его диагональ и периметр
- Признаки прямоугольника
- Формулы площадей всех основных фигур
- 1. Формула площади круга через радиус или диаметр
- 2. Формула расчета площади треугольника
- 3. Площадь треугольника, формула Герона
- 4. Площадь прямоугольного треугольника по катетам
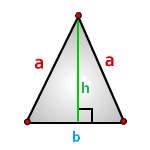
- 5. Как вычислить площадь равнобедренного треугольника ?
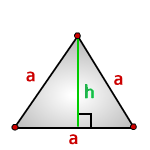
- 6. Площадь равностороннего треугольника равна:
- 7. Найти площадь треугольника, угол и две стороны
- 8. Площадь треугольника по стороне и двум углам, формула.
- 9. Формула расчета площади прямоугольника
- 10. Как рассчитать площадь квадрата через диагональ или сторону
- 11. Формулы площади параллелограмма
- 12. Площадь произвольной трапеции
- 13. Площадь равнобедренной трапеции
- Прямоугольник. Онлайн калькулятор
- Свойства прямоугольника
- Диагональ прямоугольника
- Окружность, описанная около прямоугольника
- Формула радиуса окружности описанной около прямоугольника
- Периметр прямоугольника
- Формулы сторон прямоугольника через его диагональ и периметр
- Признаки прямоугольника
Видео:Площадь треугольника через радиус описанной окружности: ОГЭ - ЕГЭСкачать

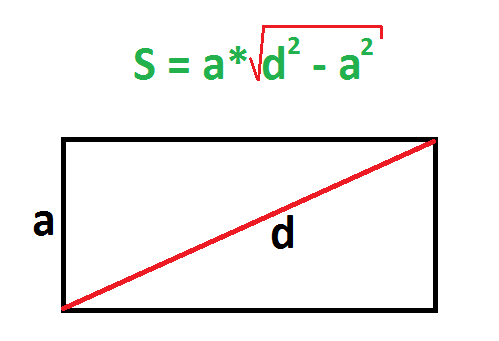
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

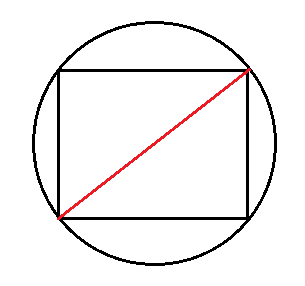
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
Видео:Радиус описанной окружностиСкачать

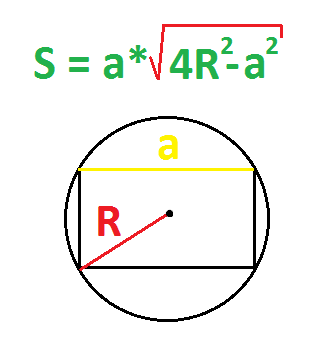
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

По стороне и периметру – 2 способ
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

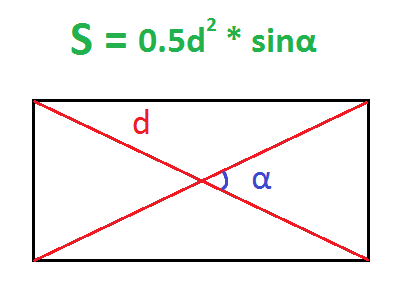
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
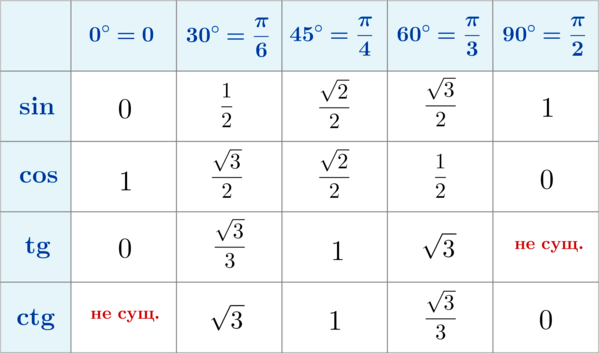
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
Видео:Площадь треугольника через радиус вписанной окружностиСкачать

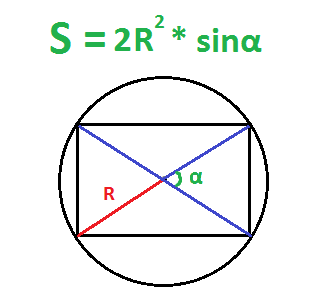
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
Видео:Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

По радиусу описанной окружности и углу между диагоналями – второй способ
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Площадь прямоугольника через окружность
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Как найти площадь прямоугольника – 9 способов с формулами и примерами
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
Видео:Площадь треугольника через периметр и радиусСкачать

По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
Видео:Формулы площади треугольника. Вписаная и описаная окружностьСкачать

По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
Видео:ЕГЭ профиль #3 / Радиус описанной окружности / прямоугольник / диагонали / решу егэСкачать

По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

По стороне и периметру – 2 способ
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
Видео:Задание 24 Площадь описанного треугольникаСкачать

По радиусу описанной окружности и углу между диагоналями – второй способ
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Видео:Найти площадь квадрата описанного около окружности радиуса 19Скачать

Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
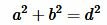 . . | (1) |
Из равенства (1) найдем d:
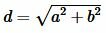 . . | (2) |
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
 |
Ответ:
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac ) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac ) | (4) |
Пример 2. Стороны прямоугольника равны 
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя 
 |
 |
Ответ:
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
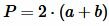 | (5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
 |
Ответ:
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
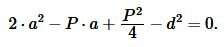 | (10) |
Вычислим дискриминант квадратного уравнения (10):
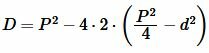 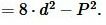 | (11) |
Сторона прямоугольника вычисляется из следующих формул:
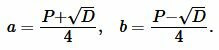 | (12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*). |
Пример 4. Диагональ прямоугольника равна 

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим 

 |
Подставляя значения 

 |
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения 

 |
Ответ: 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Формулы площадей всех основных фигур
1. Формула площади круга через радиус или диаметр
Зная диаметр или радиус круга, можно найти его площадь.
r — радиус круга
D — диаметр
Формула площади круга, (S):
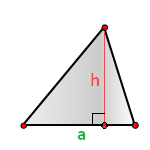
2. Формула расчета площади треугольника
h — высота треугольника
a — основание
Площадь треугольника (S):
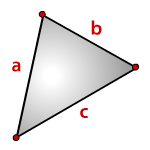
3. Площадь треугольника, формула Герона
a , b , c , — стороны треугольника
p— полупериметр, p=( a + b + c )/2
Формула ( Герона ) площади треугольника через полупериметр ( S ):
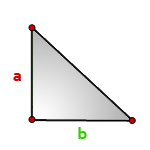
4. Площадь прямоугольного треугольника по катетам
Зная катеты прямоугольного треугольника, можно по формуле, найти его площадь.
a , b — катеты треугольника
Формула площади прямоугольного треугольника, (S):
5. Как вычислить площадь равнобедренного треугольника ?
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b , ( S ):
Формула площади треугольника через, стороны a , b , (S):

6. Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь треугольника только через сторону a , (S):
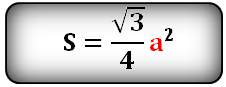
Площадь треугольника только через высоту h , ( S ):
Площадь треугольника через сторону a и высоту h , (S):
7. Найти площадь треугольника, угол и две стороны
Зная у треугольника, две стороны и синус угла между ними, находим по формуле, его площадь.
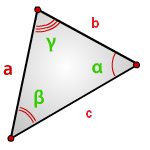
a , b , c — стороны треугольника
α , β , γ — углы
Формулы площади треугольника, через две стороны и угол между ними, ( S ):
8. Площадь треугольника по стороне и двум углам, формула.
a , b , c — стороны треугольника
α , β , γ — противолежащие углы
Площадь треугольника через сторону и два угла (S):
9. Формула расчета площади прямоугольника
b — длина прямоугольника
a — ширина
Формула площади прямоугольника, (S):
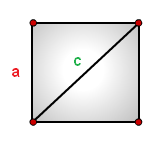
10. Как рассчитать площадь квадрата через диагональ или сторону
a — сторона квадрата
c — диагональ
Формула площади квадрата через сторону a , (S):
Формула площади квадрата через диагональ c , (S):
11. Формулы площади параллелограмма
1. Формула площади параллелограмма через стороны и углы
a, b — стороны параллелограмма
α , β — углы параллелограмма
Формула площади через стороны и углы параллелограмма, ( S ):
2. Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
Формула площади через стороны и высоты параллелограмма, (S):
3. Формула площади параллелограмма через диагонали и угол между ними
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формула площади через диагонали параллелограмма и угол между ними , (S):
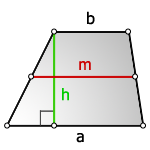
12. Площадь произвольной трапеции
1. Формула площади трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
m — средняя линия
h — высота трапеции
Формула площади трапеции, (S):
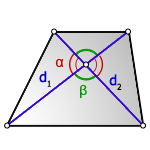
2. Формула площади трапеции через диагонали и угол между ними
d 1, d 2 — диагонали трапеции
α , β — углы между диагоналями
Формула площади трапеции, (S):
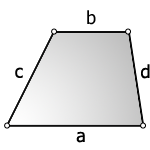
3. Формула площади трапеции через четыре стороны
b — верхнее основание
a — нижнее основание
c, d — боковые стороны
Формула площади трапеции, (S):
13. Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α , β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α , β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α , β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
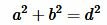 . . | (1) |
Из равенства (1) найдем d:
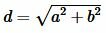 . . | (2) |
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
 |
Ответ:
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac ) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac<large sqrt> ) | (4) |
Пример 2. Стороны прямоугольника равны 
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя 
 |
 |
Ответ:
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
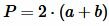 | (5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
 |
Ответ:
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
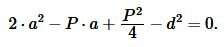 | (10) |
Вычислим дискриминант квадратного уравнения (10):
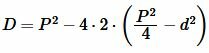 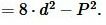 | (11) |
Сторона прямоугольника вычисляется из следующих формул:
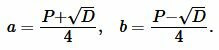 | (12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*). |
Пример 4. Диагональ прямоугольника равна 

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим 

 |
Подставляя значения 

 |
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения 

 |
Ответ: 
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.