Как сравнить два вектора unity (2 видео) | Курс школьной геометрии

DenTNT.trmw.ru

Содержание

Записная книжка
Unity: Операции с векторами
Game Dev Math. Векторы и интегралы
Векторная математика
Векторная арифметика и полезные функции
Интегралы
Как я могу сравнить два кватерниона для логического равенства?
🔍 Видео

Видео:Векторы и Манипуляции с ними, Vector3 - Unity урокиСкачать

Записная книжка

Видео:Unity 18 C# Урок 5 - Векторы и Манипуляции с ними, Vector3Скачать

Unity: Операции с векторами

В одном из проектов мне встретился такой код:

здесь transform.forward представлен как Vector3,
moveSpeed и Time.deltaTime — float
Т.е. тут идет умножение ненулевого ВЕКТОРА на число. Поскольку я учился на физмате, то сейчас у меня чуть не съехала крыша, когда я пытался вспомнить все то, что я знаю о векторах, ведь если вернутся к математике, формула выше решается так:

Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа. OnlineMSchool

К счастью, до того, как окончательно треснул мой череп, я успел понять, что Vector3 в Unity — это не совсем ВЕКТОР (отрезок, имеющий направление), здесь это прежде всего КООРДИНАТЫ x, y для Vector2 и x. y, z — для Vector3. Хотя наверное на вектор это похоже, т.к. начало его лежит в точке 0.
В документации Unity есть несколько статей про операции с векторами:
1. Понимание векторной арифметики
2. Направление и расстояние от одного объекта до другого
3. Вычисление нормали/перпендикуляра
4. Величина одного вектора, лежащая в направлении другого вектора

Видео:Unity/C# Векторы, модуль, направлениеСкачать

Game Dev Math. Векторы и интегралы

Сегодня хотелось бы поговорить о математике. Математика очень интересная наука и она может сильно пригодиться при разработке игр, да и в целом при работе с компьютерной графикой. Многие (особенно новички) просто не знают о том, как она применяется при разработке. Существует множество задач, не требующих глубокого понимания таких понятий как: интегралы, комплексные числа, группы, кольца и др, но благодаря математике вы можете решать многие интересные задачи. В этой статье мы рассмотрим векторы и интегралы. Иллюстрирующий Unity проект прилагается.

Видео:Unity For Beginners - Vector 2 explainedСкачать

Векторная математика

Векторы и векторная математика являются необходимыми инструментами для разработки игр. Многие операции и действия завязаны на ней целиком. Забавно, что для реализации класса, который отображает стрелочку вектора в Unity, уже потребовалось большинство типовых операций. Если вы хорошо разбираетесь в векторной математике данный блок вам будет неинтересен.

Видео:Unity vector3Скачать

Векторная арифметика и полезные функции

Аналитические формулы и прочие детали легко нагуглить, так что не будем тратить на это время. Сами операции будут проиллюстрированы гиф-анимациями ниже.

Важно понимать, что любая точка в сущности является вектором с началом в нулевой точке.

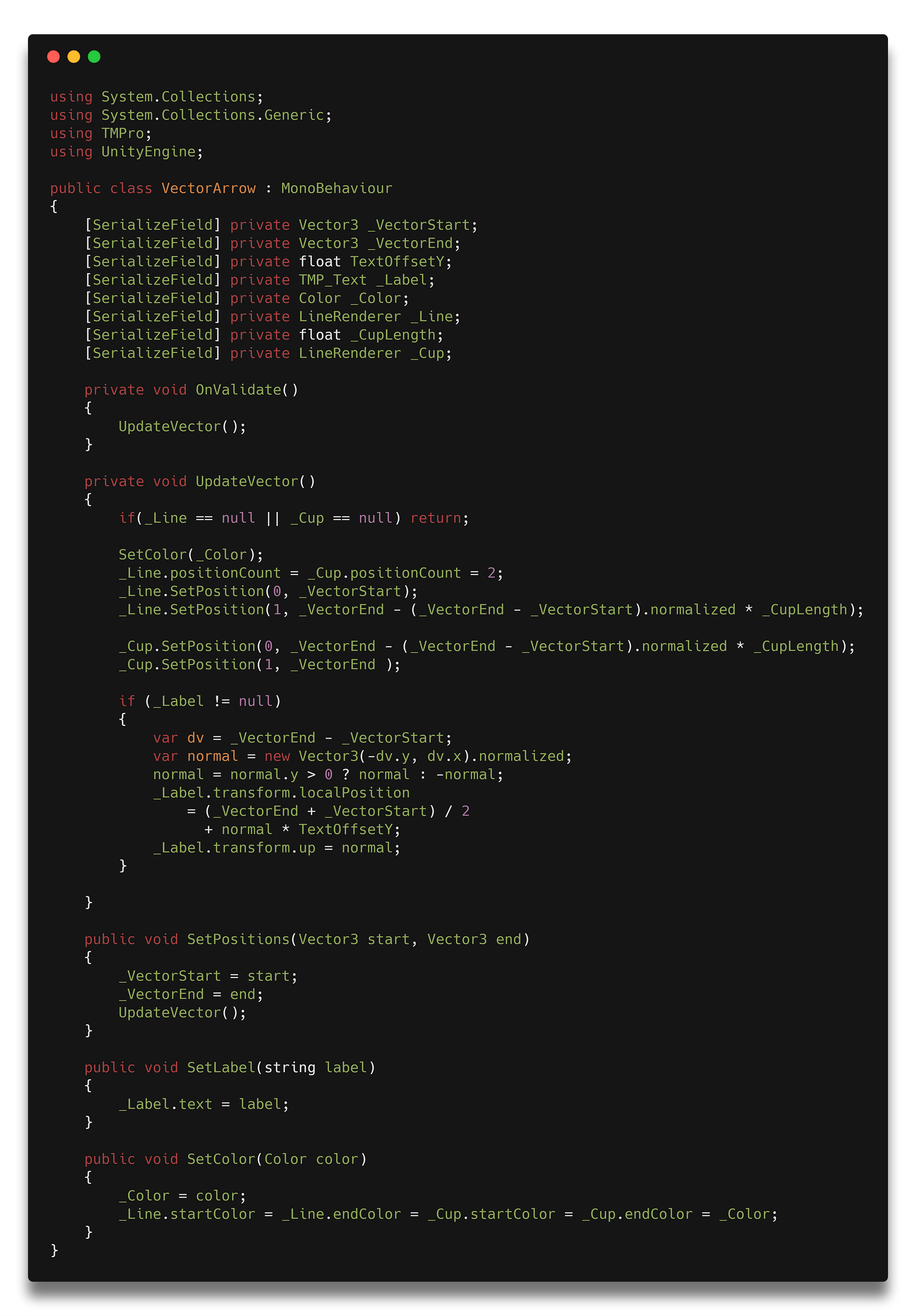
Гифки делались с помощью Unity, так что нужно было бы реализовывать класс, отвечающий за отрисовку стрелочек. Стрелка вектора состоит из трех основных компонент — линии, наконечника и текста с именем вектора. Для отрисовки линии и наконечника я воспользовался LineRenderer. Посмотрим на класс самого вектора:

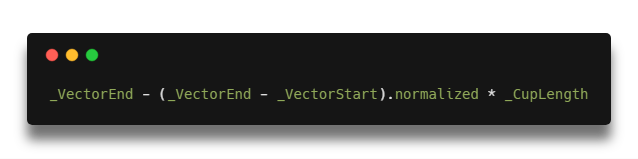
Так как мы хотим, чтобы вектор был определённой длинны и точно соответствовал точкам, которые мы задаём, то длинна линии рассчитывается по формуле:

В данной формуле (_VectorEnd — _VectorStart).normalized — это направление вектора. Это можно понять из анимации с разницей векторов, приняв что _VectorEnd и _VectorStart — это вектора с началом в (0,0,0).

Дальше разберём две оставшиеся базовые операции:

Нахождение нормали (перпендикуляра) и середины вектора — это очень часто встречающиеся задачи при разработке игр. Разберём их на примере размещения подписи над вектором.

Для того, чтобы разместить текст перпендикулярно вектору нам понадобится нормаль. В 2D графике нормаль находится достаточно просто.

Вот мы и получили нормаль к отрезку.

normal = normal.y > 0? normal: -normal ; — эта операция отвечает за то, чтобы текст всегда показывался над вектором.

Дальше остаётся поместить его в середину вектора и поднять по нормали на расстояние, которое будет смотреться красиво.

В коде использованы локальные позиции, чтобы можно была возможность двигать получившуюся стрелочку.

Но это было про 2D, а что же с 3D?

В 3D плюс-минус всё тоже самое. Отличается только формула нормали, так как нормаль уже берётся не к отрезку, а к плоскости.

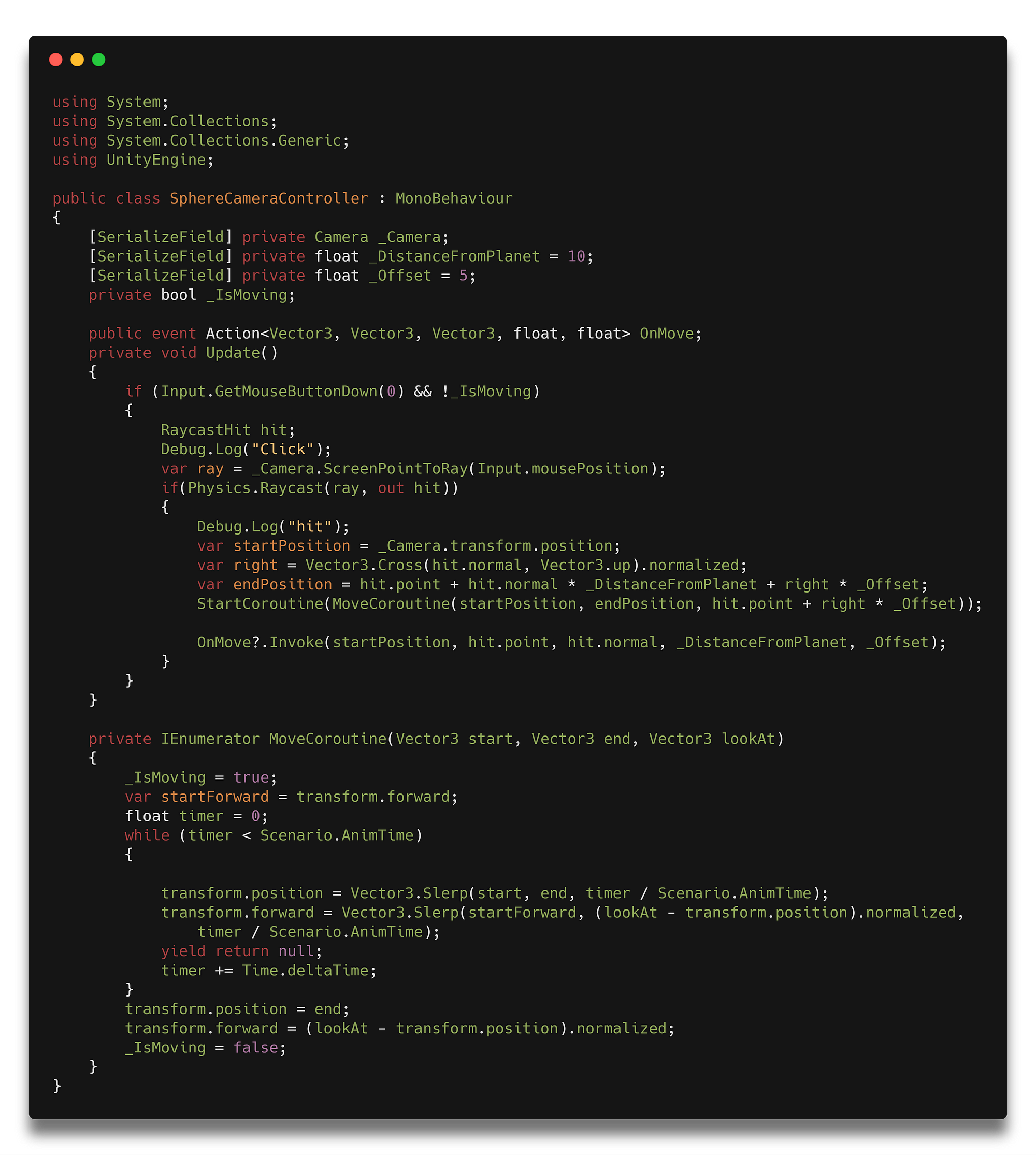
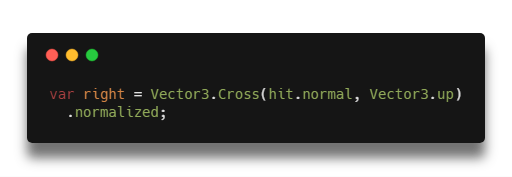
В данном примере контролла нормаль к плоскости используется, чтобы сместить конечную точку траектории право, чтобы планету не загораживал интерфейс. Нормаль в 3д графике — это нормализованное векторное произведение двух векторов. Что удобно, в Юнити есть обе эти операции и мы получаем красивую компактную запись:

Думаю, многим, кто думает, что математика не нужна и зачем вообще это знать, стало чуть понятнее какие задачи с помощью неё можно решать просто и элегантно. Но это был простой вариант, который должен знать каждый разработчик игр не стажёр. Поднимем планку — поговорим об интегралах.

Видео:Что такое Trigger и Collision | Взаимодействие объектов в UnityСкачать

Интегралы

Вообще у интегралов очень много применений, таких как: физические симуляции, VFX, аналитика и многое другое. Я не готов сейчас детально описывать все. Хочется описать простой и визуально понятный. Поговорим про физику.

Допустим есть задача — двигать объект в определённую точку. К примеру, чтобы при вхождении в определённый триггер, должны вылетать книги с полок. Если вы хотите двигать равномерно и без физики, то задача тривиальна и не требует интегралов, но когда книги выталкивает с полки призрак, такое распределение скорости будет смотреться совсем не так.

Что такое интеграл?

По сути это площадь под кривой. Но что это означает в контексте физики? Допустим у вас есть распределение скорости по времени. В данном случае площадь под кривой — это путь который пройдёт объект, а это как раз то, что нам и нужно.

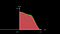
Если перейти от теории к практике, то в Unity есть замечательный инструмент под названием AnimationCurve. С помощью него можно задать распределение скорости с течением времени. Создадим вот такой класс.

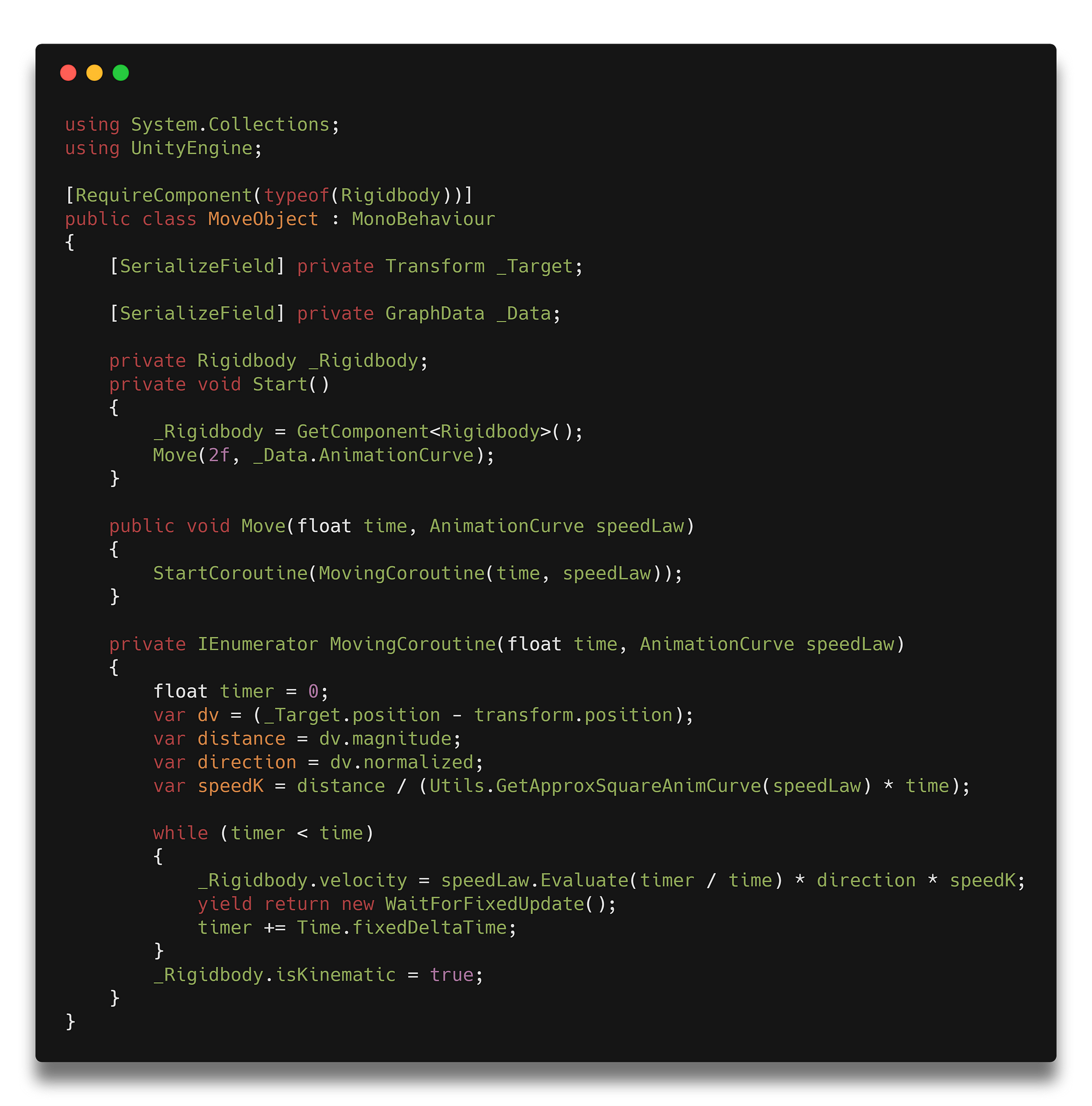
Метод GetApproxSquareAnimCurve — это и есть наше интегрирование. Мы делаем его простейшим численным методом, просто идём по значениям функции и суммируем их определённое число раз. Я выставил 1000 для верности, в целом можно подобрать оптимальнее.

Благодаря этой площади мы дальше уже знаем, какое относительное расстояние. А дальше сравнив два пройденных пути мы получаем коэффициент скорости speedK, который отвечает за то, чтобы мы прошли заданное расстояние.

Можно заметить, что объекты не совсем совпадают, это связано с ошибкой float. В целом можно пересчитать тоже самое в decimal, а потом перегнать в float для большей точности.

Собственно на этом на сегодня всё. Также вот ссылка на GitHub проект, в котором все исходники по данной статье. И с ними можно поиграться.

Видео:Unity Как узнать угол между двумя объектамиСкачать

Как я могу сравнить два кватерниона для логического равенства?

Я пытаюсь написать несколько юнит-тестов и понимаю, что не знаю, как сравнивать кватернионы. Мне нужно знать, представляют ли два кватерниона одинаковую ориентацию (объект будет смотреть одинаково). С векторной позицией я бы просто сравнил детали и проверил, что они достаточно близки, но для кватернионов значения могут сильно отличаться.

Как я могу сравнить два кватерниона?

Если ваши два кватерниона равны q1 и q2 , они представляют один и тот же поворот, если выполняется любое из этих двух условий:

q1 компонентный примерно равен q2 ИЛИ
q1 компонентный примерно равен -q2

Зная это, вы можете написать довольно упрощенный тестер равенства, который соответствует вашей цели.

Просто потому, что это не было упомянуто. Поскольку кватернионы, используемые для пространственной ориентации, всегда имеют единичную длину (или должны быть), будет также работать следующее.

где EPS — некоторый коэффициент выдумки, чтобы учесть небольшие ошибки из-за ограниченной точности с плавающей запятой. Если (и только если) оба кватерниона представляют одну и ту же ориентацию, то q1 = +- q2 и так q1.dot(q2) = +- 1 . Если вы хотите убедиться, что они имеют одинаковое вращение (а не просто ориентацию), то удалите abs .

Кватернионы хранятся как 4 числа с плавающей точкой или двойные, часто называемые x, y, z и w, где первые три представляют ось, а w — степень вращения вокруг этой оси.

Наивным подходом было бы просто сравнить эти числа двух кватернионов на равенство. Однако, поскольку вычисления с плавающей запятой связаны с ошибкой, вы должны по крайней мере использовать ошибку, часто называемую eps (для epsilon), и сравнивать каждый компонент следующим образом.

Лучшим тестом было бы рассчитать скалярное произведение двух кватернионов и проверить, близко ли оно к 1,0. Вы должны посмотреть на уравнение кватернионов с sin и cos и просто поставить два кватерниона, тогда вы должны легко понять, почему это работает.