Этот калькулятор оценивает число малых окружностей заданного радиуса r можно разместить внутри большой окружности заданного радиуса R.
Этот калькулятор выводит максимальное число малых окружностей заданного радиуса r можно разместить внутри большой окружности заданного радиуса R. Например это могут быть малые трубы внутри большой, провода в кабель канале, круги, вырезаемые из круговой же заготовки и так далее.
Вы можете подумать, что для решения такой задачи должна быть выведена формула, но на самом деле это не так — формулы нет. Эта задача относится к классу оптимизационных задач, а точнее, задач упаковки. Эта задача известна как Упаковка кругов в круге. Упаковка кругов в круге — это двумерная задача упаковки, целью которой является упаковка единичных кругов в как можно меньший круг. См. Упаковка кругов в круге.
Для этой задачи найденное решение еще и должно быть проанализировано на оптимальность. Статья в википедии по ссылке выше приводит первые 20 решений (иными словами, приводит минимальные радиусы больших окружностей вмещающих заданное число единичных окружностей. Между прочим, по умолчанию входные параметры калькулятора дают ответ 11 кругов, что соответствует следующей диаграмме:
Хорошей новостью является то, что есть проект в интернете, целиком посвященный задачам упаковки — сайт Packomania. На сегодняшний день он содержит все найденные решения, автор сайта, Экард Спехт (Eckard Specht), сам участвует в поиске решений, и большинство решений, на самом деле найдены им. Оттуда можно взять соотношения r к R для решений, позволяющих упаковать от 1 до 2600 окружностей внутри большой, с графическими диаграммами решения.
Соотношения r/R, приведенные на сайте и использует калькулятор ниже для поиска оптимального решения. Если соотношение не попадает в диапазон известных решений, калькулятор выдает ошибку.
- Сколько окружностей в прямоугольнике
- Прямоугольник. Онлайн калькулятор
- Свойства прямоугольника
- Диагональ прямоугольника
- Окружность, описанная около прямоугольника
- Формула радиуса окружности описанной около прямоугольника
- Периметр прямоугольника
- Формулы сторон прямоугольника через его диагональ и периметр
- Признаки прямоугольника
- Вписанная окружность
- Свойства вписанной окружности
- В треугольник
- В четырехугольник
- Примеры вписанной окружности
- Верные и неверные утверждения
- Окружность вписанная в угол
- Что такое прямоугольник: определение, свойства, признаки, формулы
- Определение прямоугольника
- Свойства прямоугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Признаки прямоугольника
- Формулы
- Вписанная окружность
- Свойства вписанной окружности
- В треугольник
- В четырехугольник
- Примеры вписанной окружности
- Верные и неверные утверждения
- Окружность вписанная в угол
- 📺 Видео
Видео:Три окружности в прямоугольнике.Скачать
Сколько окружностей в прямоугольнике
Видео:Геометрия В прямоугольнике ABCD известно, что AB = 12 см, угол CAD = 30. Найдите радиус окружностиСкачать

Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Видео:№708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любойСкачать

Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Видео:В любой прямоугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
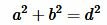 . . | (1) |
Из равенства (1) найдем d:
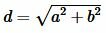 . . | (2) |
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
 |
Ответ:
Видео:Любой прямоугольник можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Видео:Геометрия Докажите, что если в прямоугольник можно вписать окружность, то этот прямоугольникСкачать

Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac ) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac ) | (4) |
Пример 2. Стороны прямоугольника равны 
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя 
 |
 |
Ответ:
Видео:Если в четырёхугольник можно вписать окружностьСкачать

Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
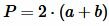 | (5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
 |
Ответ:
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
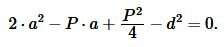 | (10) |
Вычислим дискриминант квадратного уравнения (10):
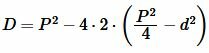 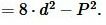 | (11) |
Сторона прямоугольника вычисляется из следующих формул:
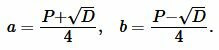 | (12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*). |
Пример 4. Диагональ прямоугольника равна 

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим 

 |
Подставляя значения 

 |
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения 

 |
Ответ: 
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Видео:Длина окружности. Математика 6 класс.Скачать

Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Что такое прямоугольник: определение, свойства, признаки, формулы
В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Определение прямоугольника
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
- длины – более длинная пара сторон. Обычно обозначаются латинской буквой, например, a;
- ширины – более короткая пара сторон. Чаще всего обозначаются как b.
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Видео:Прямоугольник. Что такое прямоугольник?Скачать

Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.
- a– это высота h1, проведенная к стороне b
- b– это высота h2, проведенная к стороне a
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.
Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d 2 = a 2 + b 2
Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.
Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Видео:Математика 2 класс (Урок№36 - Прямоугольник.)Скачать

Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
- Его диагонали равны.
- Все его углы равны.
- Если квадрат диагонали равен сумме квадратов его смежных сторон.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Формулы
1. Площадь прямоугольника (S):
2. Периметр прямоугольника (P):
Видео:Периметр прямоугольника. Как найти периметр прямоугольника?Скачать

Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac(a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
📺 Видео
найти сторону четырехугольника, в который вписана окружностьСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / прямоугольник / диагонали / решу егэСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать















