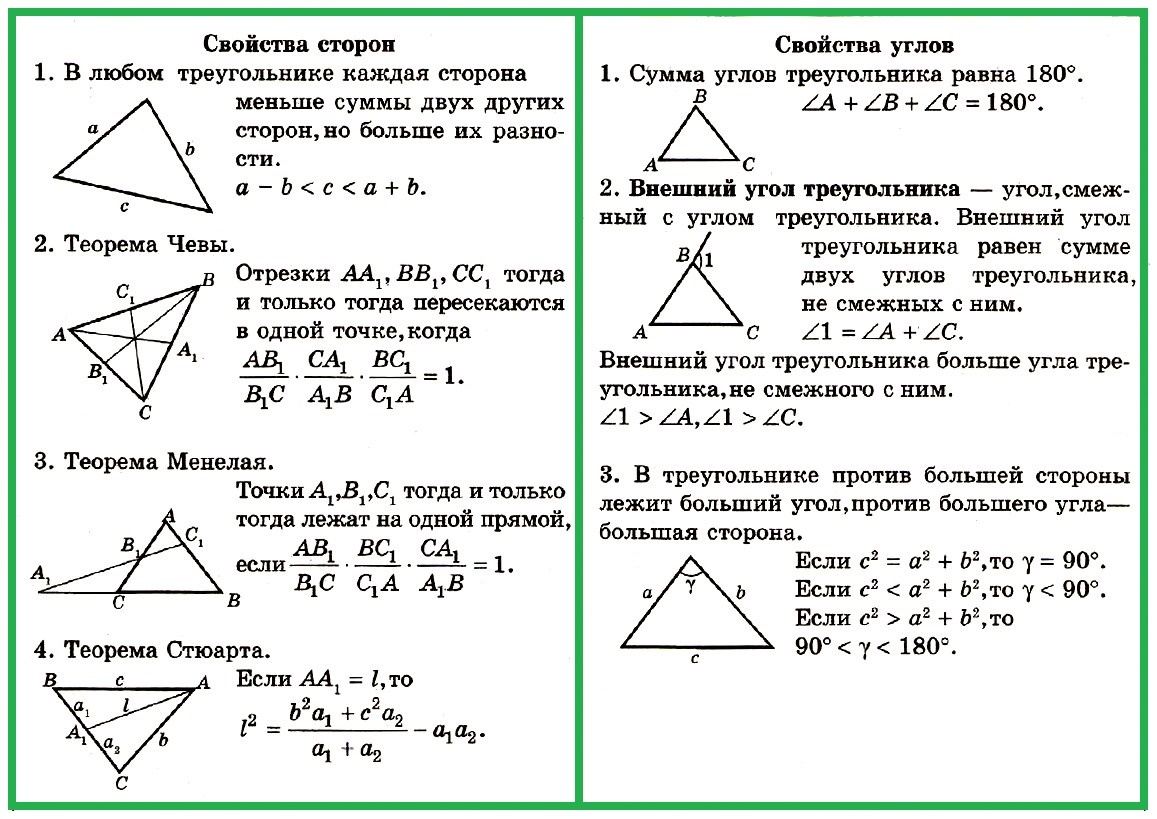
Внешний угол треугольника задачи (4 видео)

Внешний угол треугольника задачи

Свойства углов
1. Сумма углов треугольника равна 180°.
2. Внешний угол треугольника — угол, смежный с углом треугольника.
3. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
4. Внешний угол треугольника больше угла треугольника, не смежного с ним.
5. В треугольнике против большей стороны лежит больший угол, против большего угла — большая сторона.

Содержание

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
Задачи по геометрии по темам:»Внешний угол треугольника. Параллельность прямых» 7 класс
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Теорема о внешнем угле треугольника: формулировка и задачи
Определение внешнего угла
Формулировка теоремы
Примеры задач
🔥 Видео

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

Задача № 1. Дано: AB = BC, CD AB, ∠ABC = 32. Найти: ∠ACD

Задача № 2. Дано: ABC, AB = BC, ∠DBC — внешний угол ABC, ∠DBC = 52. Найти: ∠BAC, ∠BCA.

Задача № 3. Дано: ABC, AB = BC, ∠C = 64, AD — биссектриса ∠A. Найти: ∠ADB.

Задача № 4. Дано: AD = DB, BK = KC, ∠BAD = 38, ∠BCK = 26. Найти: ∠BDK, ∠BKD, ∠DBK.

Это конспект по теме «Свойства сторон и углов треугольника». Выберите дальнейшие действия:

Видео:Внешний угол треугольникаСкачать

Задачи по геометрии по темам:»Внешний угол треугольника. Параллельность прямых» 7 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:7 класс. Внешний угол треугольника.Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

§ 12. Сумма внутренних углов треугольника.
Свойство внешнего угла треугольника.

Сумма внутренних углов треугольника.

230. 1) Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один угол прямой, а другой острый?

2) Какому условию должна удовлетворять сумма острого и тупого углов тупоугольного треугольника?

231. 1) Можно ли построить треугольник, чтобы каждый его угол был:
а) меньше 60°, б) больше 60°?

2) Может ли треугольник иметь такие внутренние углы:
а) 78°, 56°, 63°; б) 42°, 89°, 49°?

232. Один из острых углов прямоугольного треугольника равен:
а) 48°; б) 17°18′; в) 63°4’28». Вычислить другой острый угол.

233. В треугольнике два угла равны 47° и 56°. Вычислить третий угол.

234. Точка D, взятая внутри треугольника ABC, соединена с вершинами Aи С. Доказать, что угол ADC больше угла AВС.

235. Какой вид имеет треугольник, если:
а) один из его углов равен сумме двух других углов;
б) один из его углов больше суммы двух других углов?

236. В остроугольном треугольнике ABC / В = 70°. Из вершины угла Aпроведена высота AD. Найти углы образовавшегося треугольника ABD.

237. В треугольнике ABC / А = 65°, / В = 73°. Определить углы, которые образует высота треугольника, проведённая из вершины С, со сторонами АС и ВС.

238. На чертеже 94 отрезки ЕС и BD пересекаются в точке А, / D = / C.
Доказать, что / В = / Е.

239. В треугольнике ABC (черт. 95) проведён отрезок MN так, что / 1 = / 2. Доказать, что / 3 = / 4.

240. На чертеже 96 / 2 = / 3. Доказать, что / 1 = / 4.

241. Из точки, взятой вне прямой, проведены к ней две наклонные, образующие между собой угол, равный 60°. Длина каждой наклонной равна 18 см. Найти проекции наклонных на эту прямую.

242. Из точки, взятой вне прямой, проведены к ней две наклонные, образующие с ней углы, равные 60°. Расстояние между основаниями наклонных равно 16 см. Найти длины наклонных.

243. Угол при вершине равнобедренного треугольника равен: а) 72°; б) 16°48′. Вычислить угол при его основании.

244. Один из углов при основании равнобедренного треугольника равен:
а) 17°; б) 46°17′. Вычислить угол при его вершине.

245. Биссектриса угла при вершине равнобедренного треугольника составляет с боковой стороной угол, равный 15°24′. Найти все внутренние углы треугольника.

246. В равнобедренном треугольнике высота, проведённая к основанию, в два раза меньше этого основания. Найти углы треугольника.

247. На чертеже 97 изображена фигура, состоящая из квадрата и равностороннего треугольника. Найти величину углов 1, 2, 3 и 4.

248. Доказать, что треугольник будет прямоугольным, если медиана треугольника, проведённая к большей его стороне, равна её половине.

249. В треугольнике ABC / А= 35°, / В = 68°. Через вершину В проведён отрезок BD (точка D лежит на стороне АС) так, что ВС = CD. Найти меньший из углов, вершины которых находятся в точке D.

250. В треугольнике ABC (черт. 98). / 1 = 55°, / 2 = 84°. Прямая DE пересекает треугольник ABC так, что / 3 = 140°. Определить углы треугольников BDF и CDE.

251. В треугольнике ABC / А = 65°, / В = 73°. Биссектриса CD угла С делит треугольник на два треугольника — CBD и ACD. Определить углы этих треугольников.

252. В треугольнике два угла равны соответственно 65° и 42°. Найти, под каким углом пересекаются биссектрисы этих углов.

253. В треугольнике ABC / A = 44°, / В = 57°. Определить, под каким углом пересекаются биссектрисы углов А и С.

254. 1) Острый угол прямоугольного треугольника равен 24°. Найти углы, образованные биссектрисами этого и прямого углов треугольника.

2) Найти углы между биссектрисами острых углов прямоугольного треугольника.

255. 1) Найти, под каким углом пересекаются биссектрисы двух углов треугольника, если третий угол равен 28°.

2) Найти, под каким углом пересекаются биссектрисы острых углов тупоугольного треугольника, если тупой угол равен 135°.

256. В треугольнике ABC / А= 42°, / В = 86°. Через вершины А и В проведены прямые, параллельные противоположным сторонам треугольника. Найти меньший из углов, образованных этими прямыми.

257. 1) В треугольнике ABC / А = 60°, / С = 72°. Определить меньший угол между высотами, проведёнными через вершины углов А и С.

2) Найти меньший угол между двумя высотами равностороннего треугольника.

258. Построить прямоугольный треугольник:
а) по катету, равному 6,2 см, и противолежащему углу, равному 65°;
б) по гипотенузе, равной 6,5 см, и острому углу, равному 42°.

259. Построить прямоугольный треугольник:
а) по катету а и противолежащему углу α;
б) по гипотенузе с и острому углу α.

260. Построить равнобедренный прямоугольный треугольник по его гипотенузе.

261. Доказать, что равнобедренные треугольники равны, если у них равны основания и углы при вершине.

262. Измерить длины всех высот прямоугольного треугольника, гипотенуза которого равна 6 см, а острый угол равен 40°.

263. Два отрезка АВ и CD пересекаются в точке О и делятся в этой точке пополам. Точки А и D и точки С и В соединены отрезками прямых. Доказать, что точка О одинаково удалена от отрезков AD и СВ.

264. В треугольнике ABC через вершину С проведена медиана CD. Доказать, что высоты треугольников DBC и DAC, проведённые из вершин В и А, равны.

265. Даны точки А, В и С, не лежащие на одной прямой. Через точку В провести прямую так, чтобы отрезки перпендикуляров, проведённых из точек С и Ак этой прямой до пересечения с ней (расстояния от точек С и Адо прямой), были бы равны между собой.

Свойство внешнего угла треугольника.

266. Один из внешних углов треугольника равен 95°. Чему равна сумма двух внутренних углов, с ним не смежных?

267. 1) В треугольнике ABC / C = 35°, внешний угол треугольника при вершине В равен 72°. Определить все внутренние углы треугольника ABC.

2) Внешний угол прямоугольного треугольника равен 128°. Найти его острые углы. Задача эта может быть решена двумя способами. Укажите их.

268. 1) Какое соотношение существует между внутренним углом при основании равнобедренного треугольника и его внешним углом при вершине?

2) Может ли внешний угол при основании равнобедренного треугольника быть: прямым, острым, тупым?

3) Если один из внешних углов треугольника острый, то какими являются остальные внешние углы треугольника? Почему?

269. Доказать, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию треугольника.

270. 1) Внешний угол при вершине равнобедренного треугольника равен 68°. Найти углы при основании треугольника.

2) Внешний угол при вершине равнобедренного треугольника равен 162°. Найти внешний угол при основании треугольника.

271. В треугольнике ABC / А = 48°, / В = 56°. На продолжении АС отложены отрезки СЕ и AD (черт. 99) так, что ВС = СЕ и AD = АВ. Найти углы треугольника BDE.

272. Две прямые образуют с третьей прямой углы, равные 48° и 63°. Вычислить величину меньшего угла, образованного этими прямыми. Сколько решений имеет задача? Выполнить для каждого случая чертёж.

273. Внешний угол треугольника равен 90°. Найти величину каждого из внутренних углов, не смежных с ним, если они относятся, как 3 : 5.

274. 1) Два внутренних угла треугольника равны 62° и 105°. Вычислить сумму их внешних углов.

2) Сумма двух внешних углов треугольника равна 258°. Чему равен внутренний угол треугольника, не смежный ни с одним из них?

275.1) На чертеже 100 АВ || CD, отрезки AD и СВ пересекаются в точке О. Найти угол BOD.

2) Доказать, что / 3 = / l + / 2, если АВ || CD (черт. 101).

276. В треугольнике ABC / В = 110°, / C = 50°, AD — высота треугольника. Доказать, что / DAC = 2 / DAB.

277. В равнобедренном треугольнике сумма внутренних углов вместе с одним внешним составляет 310°. Определить внутренние углы треугольника (два решения).

278. В треугольнике ABC (черт. 102) проведён отрезок BD так, что АВ = AD. Внешний угол при вершине А равен 140°, а угол С равен 35°. Доказать, что BD = DC.

279. Пользуясь чертежом 103, доказать, что AD = АВ, если DC || AB.

Свойство катета, лежащего против угла в 30°.

280. Биссектриса угла при вершине равнобедренного треугольника образует с его стороной угол в 60°. Определить высоту треугольника, если его боковая сторона равна
25 см.

281. Найти неизвестные размеры отрезков на чертежах 104 и 105.

282. 1) В прямоугольном треугольнике один из углов равен 60° ,сумма гипотенузы и меньшего катета равна 45 см. Найти длину гипотенузы.

2) Построить прямоугольный треугольник, если один из его углов равен 60°, а гипотенуза на 5,5 см больше его меньшего катета.

283. Отрезок длиной 15 см образует с некоторой прямой угол в 60°. Найти проекцию этого отрезка на эту прямую.

284. Из точки, взятой на расстоянии 10 см от прямой, проведены к прямой две наклонные, длины которых относятся, как 1 : 2. Меньшая наклонная образует с прямой угол, равный 30°. Определить длины наклонных.

285. Построить равносторонний треугольник по его высоте.

231. 1) а) Нет; б) Нет. 232. б) 72°42′; в)26°55’32». 233. 77°. 236. 70°, 20°, 90°. 237. 25° и 17°. 241. 9 см. 242. 16 см. 243. а) 54°; б) 81°36′. 244. а) 146°; б)87°46′.
245. 30°48′;74°36′;74°36′. 246. 45°, 45°, 90°. 247. 15°, 150°, 75°, 30°. 249. 51°30′.
250. 15°, 40°, 125°, 40°, 41°, 99°. 251. 21°, 73°, 86° и 21°, 65°, 94°. 252. 126° 30′.
253. 118° 30′. 254. 1) 123° и 57°; 2) 135° и 45°. 255. 1) 104°; 2) 157° 30′. 256. 52°.
257. 1) 48°; 2) 60°. 262. 3,0 см 3,9 см, 4,6 см. 266. 95°. 267. 1) 35°, 108°, 37°; 2) 52°, 38°. 270. 1) 34°; 2) 99°. 271. 24°, 38°, 118°. 272. 69° или 15°. 273. 33°45′, 56°15′.
274. 1) 193°; 2) 78°. 275. 1) 85°. 277. 65°, 65°, 50° или 50°, 50°, 80°. 280. 12,5 см.
281.30 мм, 25 мм. 283. 7,5 см. 284. 20 см и 40 см.

Видео:Внешний угол треугольникаСкачать

Теорема о внешнем угле треугольника: формулировка и задачи

В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.

Видео:теорема о внешнем угле треугольника. Доказательство.Скачать

Определение внешнего угла

Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:

Смежный с внутренним углом ( λ ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ .

γ + λ = 180°

Видео:Внешний угол треугольника. Теорема о внешнем угле треугольника. Примеры задач. Геометрия 7 класс.Скачать

Формулировка теоремы

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.

Видео:Внешний угол треугольникаСкачать

Примеры задач

Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.

Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.

Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.

Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α .

Исходя из теоремы: β = γ – α = 115° – 28° = 87° .

Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65° .