Площадь параллелепипеда через вектора

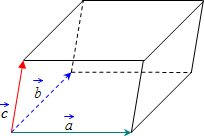
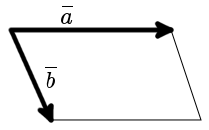
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:

Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:

Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.

Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.

Видео:Найдите площадь параллелограмма, построенного на векторахСкачать

Онлайн калькулятор. Площадь параллелограмма построенного на векторах.

Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.

Видео:Площадь параллелограмма по векторамСкачать

Калькулятор для вычисления площади параллелограмма построенного на векторах

Выберите каким образом задается параллелограмм:

Введите значения векторов: Введите координаты трех любых вершин параллелограмма:

Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах

Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Теория. Площадь параллелограмма построенного на векторах.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:10 класс, 44 урок, Правило параллелепипедаСкачать

Ориентированные площади и объёмы

Видео:Правило параллелепипеда для векторовСкачать

Ориентированная площадь параллелограмма

Ориентированной площадью параллелограмма , построенного на неколлинеарных векторах и , называется его площадь , взятая со знаком плюс, если ориентация пары векторов и правая , и со знаком минус, если ориентация — левая

Внешним (косым) произведением неколлинеарных векторов и на плоскости называется число, равное ориентированной площади параллелограмма, построенного на этих векторах. Если векторы и коллинеарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается . Его свойства повторяют алгебраические свойства векторного произведения, т.е. для любых векторов на плоскости и любого числа справедливы равенства:

4) Если векторы и в правом ортонормированием базисе имеют координаты и соответственно, то внешнее произведение этих векторов находится по формуле

Если — координатные столбцы векторов в стандартном базисе на плоскости, то их внешнее произведение находится по формуле

Приведенные свойства внешнего произведения следуют из алгебраических свойств векторного произведения, если векторы на плоскости рассматривать как векторы в пространстве с нулевыми аппликатами.

Рассмотрим задачу разложения вектора по базису на плоскости. Отложим все векторы от произвольной точки . Сначала разберем случаи, когда векторы и коллинеарны: одинаково направлены (рис.1.49,а) или противоположно направлены (рис. 1.49,6). В этих случаях ордината вектора равна нулю, а абсцисса находится как отношение

так как пара в первом случае правая (рис.1.49,а), а во втором случае — левая (рис.1.49,б).

Пусть теперь векторы и не коллинеарны (рис.1.49,в). Построим проекции и на прямые, содержащие базисные векторы: . Из концов векторов и опустим перпендикуляры и соответственно на прямую, содержащую вектор . Учитывая, что векторы и противоположно направлены, а также подобие прямоугольных треугольников с гипотенузами и , находим абсциссу вектора :

так как пара — правая, а пара — левая. Аналогично находится ордината (векторы и одинаково направлены)

Таким образом, вектор имеет следующее разложение по базису на плоскости:

Рассмотрим применение формулы (1.19) для решения системы двух линейных уравнений с двумя неизвестными:

Эту систему можно записать в виде .Рассматривая полученные столбцы как координатные столбцы векторов в стандартном базисе на плоскости, получаем разложение .

Таким образом, нахождение решения системы уравнений свелось к задаче разложения вектора по векторам и . Предполагая, что коэффициенты при неизвестных не пропорциональны, т.е. (векторы и не коллинеарны), по формуле (1.19), полагая , получаем:

Видео:44. Правило параллелепипедаСкачать

Ориентированный объем параллелепипеда

Ориентированным объемом параллелепипеда , построенного на некомпланарных векторах , называется его объем , взятый со знаком плюс, если ориентация тройки векторов правая и со знаком минус, если ориентация — левая .

Внешним (косым) произведением некомпланарных векторов называется число, равное ориентированному объему параллелепипеда, построенного на этих векторах. Если векторы компланарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается .

Внешнее произведение трех векторов совпадает с их смешанным произведением (в силу первого геометрического свойства смешанного произведения), т.е. . В ортонормированием базисе

так как определитель транспонированной матрицы равен определителю исходной матрицы.

При помощи ориентированных объемов задача разложения вектора по базису в пространстве решается так же как и на плоскости с использованием ориентированных площадей. В результате получаем

Формула (1.21) соответствует правилу Крамера решения системы трех линейных уравнений с тремя неизвестными.

Пример 1.23. Заданы координатные столбцы

векторов в стандартном базисе. Разложить вектор по векторам .

Решение. По формуле (1.20) находим смешанные произведения

Коэффициенты разложения определяем по формуле (1.21):

🎬 Видео

§20 Нахождение объёма параллелипипедаСкачать

как найти площадь параллелограмма построенного на векторахСкачать

18+ Математика без Ху!ни. Векторное произведение.Скачать

1. Векторы и параллелограмм задачи №1Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Задача 4. Вычислить площадь параллелограмма, построенного на векторах.Скачать

Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Найти угол между векторами и площадь параллелограмма, построенного на этих векторахСкачать

Площадь треугольника, построенного на векторахСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

43. Компланарные векторыСкачать