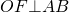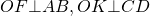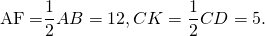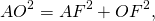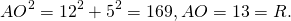Перпендикуляр опущенный к хорде из центра окружности (7 видео)

Теорема о серединном перпендикуляре к хорде

Серединный перпендикуляр к хорде проходит через центр окружности.

Серединный перпендикуляр к отрезку АВ – это множество точек, равноудаленных от точек А и В. Другими словами, все точки, равноудаленные от А и В, лежат на серединном перпендикуляре к АВ. С другой стороны, если точки А и В лежат на окружности с центром О, то АО = ВО. Это значит, что точка О лежит на серединном перпендикуляре к АВ.

Содержание

Это полезно
Расстояние от центра окружности до хорды
Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополамПОМОГИТЕ?
Докажите что диаметр окружности, проходящий через середину хорды, перпендикулярен хорде?
Докажите, что если хорда перпендикулярна радиусу окружности и делит его пополам, то она равна стороне правильного треуголбника, вписанного в эту окружность?
Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду?
Помогите пожалуйста?
Докажите, что серединный перпендикуляр к хорде окружности проходит через ее центр?
Радиус ОМ окружности с центром О делит хорду АВ пополам?
Докажите, что серединный перпендикуляр к хорде окружности проходит через центр окружности?
Помогите пожалуйста?
Докажите что перпендикуляры опущенные из цнтра окружности на две равные хорды равны между собой?
Доказать, если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, делит общую хорду пополам?
🌟 Видео

Видео:Теорема о диаметре, перпендикулярном хордеСкачать

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Расстояние от центра окружности до хорды

Рассмотрим, как найти расстояние от центра окружности до хорды.

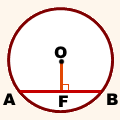
Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из этой точки на данную прямую. Значит, расстояние от центра окружности до хорды равно длине перпендикуляра, проведённого из центра окружности к этой хорде.

Например, расстояние от точки O — центра окружности — до хорды AB равно длине перпендикуляра OF:

Отрезки AB и CD являются хордами окружности. Найти расстояние от центра окружности до хорды CD, если AB=24, CD=10, а расстояние от центра окружности до хорды AB равно 5.

Дано: окружность (O; R), AB и CD — хорды,

1) Соединим центр окружности с концами хорд.

2) Треугольники AOB и COD — равнобедренные с основаниями AB и CD (AO=BO=CO=DO как радиусы).

Значит, их высоты OF и OK являются также медианами. Следовательно,

3) Рассмотрим треугольник AOF, где ∠AFO=90 º.

4) Рассмотрим треугольник COK, где ∠CKO=90 º.

Видео:Демо-вариант ОГЭ по математике, задача 10Скачать

Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополамПОМОГИТЕ?

Геометрия | 5 — 9 классы

Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополам

Надеюсь, все понятно написано.

Видео:ОГЭ вариант-4 #24Скачать

Докажите что диаметр окружности, проходящий через середину хорды, перпендикулярен хорде?

Докажите что диаметр окружности, проходящий через середину хорды, перпендикулярен хорде.

Видео:Геометрия Перпендикуляр, опущенный из точки окружности на ее диаметр, делит его на два отрезка, одинСкачать

Докажите, что если хорда перпендикулярна радиусу окружности и делит его пополам, то она равна стороне правильного треуголбника, вписанного в эту окружность?

Докажите, что если хорда перпендикулярна радиусу окружности и делит его пополам, то она равна стороне правильного треуголбника, вписанного в эту окружность.

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду?

Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду.

Видео:Задание 24 ОГЭ по математике #6Скачать

Помогите пожалуйста?

Докажите, что если две окружности имеют общую хорду, то прямая проходящая через центры окружности делят общую хорду пополам.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Докажите, что серединный перпендикуляр к хорде окружности проходит через ее центр?

Докажите, что серединный перпендикуляр к хорде окружности проходит через ее центр.

Можно с рисунком, пожалуйста.

Видео:ОГЭ вариант-3 #10Скачать

Радиус ОМ окружности с центром О делит хорду АВ пополам?

Радиус ОМ окружности с центром О делит хорду АВ пополам.

Докажите, что касательная, проведенная через точку М, параллельна хорде АВ.

Видео:ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Докажите, что серединный перпендикуляр к хорде окружности проходит через центр окружности?

Докажите, что серединный перпендикуляр к хорде окружности проходит через центр окружности.

Видео:Окружность. 7 класс.Скачать

Помогите пожалуйста?

1. Докажите, что серединный перпендикуляр к хорде окружности проходит через центр окружности.

2. Докажите, что хорда перпендикулярная диаметру, делится диаметром на равные отрезки.

Видео:9.49.1. Планиметрия. Гордин Р.К.Скачать

Докажите что перпендикуляры опущенные из цнтра окружности на две равные хорды равны между собой?

Докажите что перпендикуляры опущенные из цнтра окружности на две равные хорды равны между собой.

О — центр окружности AB и CD — хорды.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Доказать, если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, делит общую хорду пополам?

Доказать, если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, делит общую хорду пополам.

Вы зашли на страницу вопроса Докажите, что перпендикуляр опущенный из центра окружности к хорде делит ее пополамПОМОГИТЕ?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Свойство треугольника если напротив стороны есть угол = 30° = половине гипотенузы 18 / 2 = 9см — ac.

АС = АВ * 2 = 17 * 2 = 34 АВ = АС — 10 = 34 — 10 = 24 Р(АВС) = 17 + 34 + 24 = 75 см.

1) a ^ 2 = 15 ^ 2 — 9 ^ 2 = 144a = 12.

№1 угол 1 = 138. Сумма углов параллелограмма = 360 градусов , противоположные углы равны по св — ву параллелограмма. Значит, угол 2 = 138, угол 3 = 42, угол 4 = 42.

S = 3х4х2 + 3х5х2 + 4х5х2 = 24 + 30 + 40 = 94 см2 — площадь поверхности.

Расстояние от M до вершины D — длина отрезка, соединяющего точки М и D / По данному условию задача может быть решена, если отрезокМА перпендикулярен плоскости прямоугольника. Тогда МА перпендикулярна любой прямой, лежащей в плоскости АВСD. Из прямо..

Гр — градусы соот — соответственно уг — угол сумма углов у треугольника равно 180 гр соот уг В = 180 — (30 + 75) = 75гр соот треугольник равнобедренный потому что углы при основании равны и значит что б = с = 4. 5 ну дальше уже не в курсе как.

Точки A bc el расположены как лучь поэтому они расположены на одной плоскости.

Я думаю, что так (на фото). На всякий случай сравни с ответами.

Из отношения 3 : 4 следует, что большая часть — 4 части, меньшая — 3 части 48 : 4 = 12 см длина одной части 12 * 3 = 36 см меньшая сторона Р = 2 * (a + b) P = 2 * (36 + 48) P = 2 * 84 P = 168 см.