Параллельные и перпендикулярные прямые в жизни

Презентация была опубликована 8 лет назад пользователемПолина Мымликова

Похожие презентации

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Презентация на тему: » Параллельность и перпендикулярность. Параллельные и перпендикулярные прямые играют очень большую роль в жизни человека: особенности их взаимного расположения.» — Транскрипт:

1 Параллельность и перпендикулярность

2 Параллельные и перпендикулярные прямые играют очень большую роль в жизни человека: особенности их взаимного расположения используют в строительстве, технике, искусстве. Теория параллельных занимает одно из центральных мест в науке «геометрия». Именно свойства параллельных прямых определяют основные свойства изучаемого нами пространства.

3 Рассматривая основные геометрические фигуры, среди всех углов мы выделили прямой угол, равный 90 градусов. Изобразим прямой угол и продолжим его стороны за вершину. O В А a b Мы получили две прямые, пересекающиеся под прямым углом. Две прямые, пересекающиеся под прямым углом (90°), называются ПЕРПЕНДИКУЛЯРНЫМИ.

4 Перпендикулярные прямые обладают интересными свойствами. 1. Через точку вне данной прямой можно провести только одну прямую, перпендикулярную этой прямой и пересекающую ее. 2. Если точку взять на самой прямой, то через эту точку проходит бесконечное число прямых, перпендикулярных данной прямой.

5 Если начертить прямую в тетради, то одна из прямых, перпендикулярных ей, будет лежать в плоскости тетради, а все остальные прокалывать тетрадь в данной точке. Они будут находиться в пространстве (вне плоскости листа); это похоже на дорожный столб, стоящий на перекрестке дорог: столб перпендикулярен каждой дороге (рис. 2). Рис. 2 Рис. 3 Рис. 2 Рис Две прямые на плоскости, перпендикулярные третьей прямой, не могут пересечься одна с другой (рис. 3). Если бы они пересеклись, например, в точке С, то мы получили бы треугольник ABC, у которого два прямых угла, что невозможно. На плоскости такого не может быть.

6 А вот на сфере перпендикуляры ведут себя иначе. Вспомните экватор и меридианы. Они перпендикулярны друг к другу, но все меридианы пересекаются в одной точке на ПОЛЮСЕ. Однако вернемся к плоскости. Итак, свойство 3 говорит о том, что на плоскости существуют непересекающиеся прямые. Две прямые на плоскости называются ПАРАЛЛЕЛЬНЫМИ, если они не пересекаются. a b

7 Передвигая, как показано на рисунке, треугольник вдоль неподвижной линейки, получаем множество параллельных между собой прямых. Передвигая, как показано на рисунке, треугольник вдоль неподвижной линейки, получаем множество параллельных между собой прямых. На рисунке 4-в прямые m и n параллельны. На рисунке 4-в прямые m и n параллельны. Этот факт записывается так: mn Этот факт записывается так: mn Читаем: прямая m параллельна прямой n Читаем: прямая m параллельна прямой n Выбор именно такого знака достаточно понятен, Выбор именно такого знака достаточно понятен, не так ли? б)б) Рис. 4 а б Используя линейку и чертежный угольник, можно без труда вычерчивать параллельные прямые

8 У обычного чертежного угольника один угол прямой. В этом случае с его помощью можно проводить прямые, перпендикулярные данной прямой (рис. 5). Или, как говорят, опускать на данную прямую перпендикуляры или восставлять к ней перпендикуляры. То, что прямые m и n перпендикулярны, записывается так: m n. С помощью циркуля и линейки также можно строить параллельные и перпендикулярные прямые. Предлагаемые ниже способы построения интересны и тем, что число проводимых при построении линий будет наименьшим из возможных. Рис. 5

9 Проведение параллельных прямых Пусть проведена прямая и дана точка А вне этой прямой (рис. 6). 1. Проведем через точку А любую окружность, пересекающую прямую (рис. 6). 2. Возьмем одну из точек пересечения окружности с прямой точку В, измерим циркулем отрезок АВ и проведем окружность радиусом, равным АВ, с центром в точке В 1. Появится точка А 1. Прямая, проходящая через точки А и А 1, параллельна прямой. Рис. 6

11 Проведение перпендикуляра к прямой Пусть проведена прямая и дана точка А вне этой прямой. Рис.7 Для построения перпендикуляра достаточно с помощью циркуля провести через А две произвольные окружности с центрами на прямой (рис.7). Вторая точка пересечения этих окружностей (точка А 1 ) и даст нам вторую точку на перпендикуляре. Подумайте, как провести перпендикуляр (с помощью циркуля и линейки), если точка А лежит на прямой … Поэтапное построение

12 Следует запомнить еще одно важное свойство перпендикуляра. Если А точка на прямой, а В точка пересечения перпендикулярных прямых и m (рис. 8), то, отрезок АВ есть кратчайшее расстояние от точки А до прямой m m A B Рис. 8 Итак, если мы хотим из точки А по кратчайшему пути попасть на прямую m, то двигаться надо по перпендикуляру к прямой m

13 Мы все время говорили: «параллельные прямые», «перпендикулярные прямые». Понятно, что на практике мы имеем дело не с прямыми, а лишь с их частями отрезками, лежащими на этих прямых. Отрезки, лежащие на параллельных прямых, также называются ПАРАЛЛЕЛЬНЫМИ, а на перпендикулярных — ПЕРПЕНДИКУЛЯРНЫМИ.

14 Среди ребер куба можно указать пары параллельных и перпендикулярных ребер. На рисунке 9 изображен куб. Рис. 9 С Три четверки его ребер параллельны между собой. Вот одна из них: АВ || DC || АХВХ || DXCX. 1. Назовите еще две четверки параллельных между собой ребер куба. Ребро АА 1 перпендикулярно ребрам АВ, А 1 В 1, AD и A 1 D 1. Угол между ребром АА 1 и каждым из этих ребер равен 90°. 2. Назовите ребра, перпендикулярные: а) ребру СС 1 ; б) ребру DC.

15 Ребра АА 1 и ВВ 1 куба лежат в одной плоскости в плоскости передней грани; в этой же плоскости лежат и плоскости передней грани; в этой же плоскости лежат и ребра А 1 В 1 и АВ. Рис. 9 С Через ребра АА 1 и СС 1 также можно провести плоскость АА 1 С 1 С (диагональное сечение куба).

16 А вот пара ребер АА 1 и D 1 C 1 особенная. Не существует плоскости, которая бы проходила через оба эти отрезка (а также через прямые АА 1 и D 1 C 1 ). Такие отрезки и прямые называются СКРЕЩИВАЮЩИМИСЯ. Какую бы плоскость мы ни провели через АА 1, обязательно прямая D 1 C 1 либо пересечет ее в какой-либо одной точке, либо не пересечет никогда. 3. Найдите еще несколько пар скрещивающихся ребер куба AC 1. Рис. 9 С Обозначение: ab Читают: прямые a и b — скрещивающиеся

17 За 5 мин привести как можно больше примеров: 1) параллельных прямых 2) перпендикулярных прямых, встречающихся в окружающем нас мире. Участники поочередно называют примеры таких прямых. Игра заканчивается, как только в течение минуты никто не может придумать новый пример. Побеждает тот, чей пример был последним.

18 Найдите на рисунке 9 какие-либо отрезки с концами в вершинах куба (не являющиеся его ребрами), такие, чтобы они были: а) параллельными; б) перпендикулярными; в) скрещивающимися. Рис. 9 С

19 Домашнее задание Выполнить все построения, которые выполняли на уроке, выделяя цветом главные этапы и линии, на альбомном листе А-4.

20 Спасибо за внимание! Желаю удачных построений параллельных и перпендикулярных прямых!

21 Ресурсы: И.Ф.Шарыгин, Л.Н.Еранжиева. Наглядная геометрия, 5-6 классы. Т.А.Алдамуратова, Т.С.Байшоланов. Математика. Учебник для 6 класса ОШ. Личный архив Волошина Н.Н. ГУ ШГ 5 г.Алматы

Видео:Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Параллельные прямые

Вы будете перенаправлены на Автор24

Видео:Параллельные и перпендикулярные прямые.Скачать

Понятие параллельных прямых

Параллельные прямые – прямые, которые лежат в одной плоскости, не совпадают и не имеют общих точек.

Если у прямых есть общая точка, тогда они пересекаются.

Если все точки прямых совпадают, то имеем по сути одну прямую.

Если прямые лежат в разных плоскостях, то условий их параллельности несколько больше.

При рассмотрении прямых на одной плоскости можно дать следующее определение:

Две прямые на плоскости называют параллельными, если они не пересекаются.

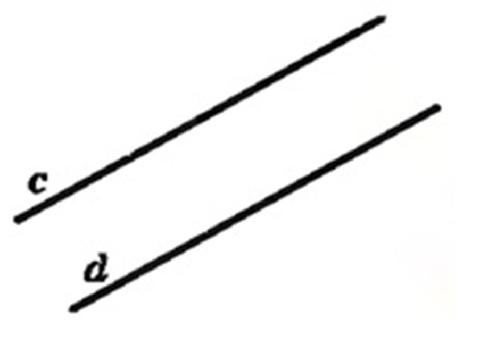
В математике параллельные прямые принято обозначать с помощью знака параллельности « $parallel$ ». Например, тот факт, что прямая $c$ параллельна прямой $d$ обозначается следующим образом:

Зачастую рассматривается понятие параллельных отрезков.

Два отрезка называют параллельными, если они лежат на параллельных прямых.

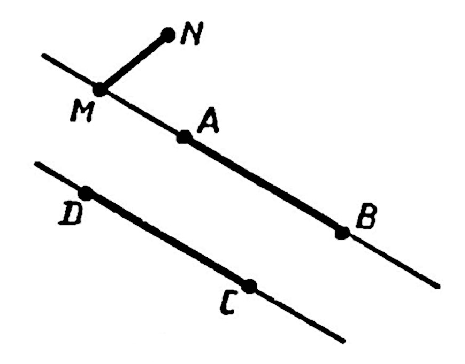
Например, на рисунке параллельными являются отрезки $AB$ и $CD$, т.к. они принадлежат параллельным прямым:

Вместе с тем, отрезки $MN$ и $AB$ или $МN$ и $CD$ параллельными не являются. Этот факт можно записать с помощью символов следующим образом:

Готовые работы на аналогичную тему

$MN ∦ AB$ и $MN ∦ CD$.

Аналогичным образом определяется параллельность прямой и отрезка, прямой и луча, отрезка и луча или двух лучей.

Видео:Параллельные и перпендикулярные прямыеСкачать

Историческая справка

С греческого языка понятие «параллелос» переводится «рядом идущий» или «проведенный друг возле друга». Этот термин использовался в древней школе Пифагора еще до того, как параллельные прямые получили свое определение. Согласно историческим фактам Евклидом в $III$ в. до н.э. в его трудах все же был раскрыт смысл понятия параллельных прямых.

В древности знак для обозначения параллельных прямых имел отличный вид того, что мы используем в современной математике. Например, древнегреческим математиком Паппом в $III$ в. н.э. параллельность обозначалась с помощью знака равенства. Т.е. тот факт, что прямая $l$ параллельна прямой $m$ ранее обозначался «$l=m$». Позднее для обозначения параллельности прямых стали использовать привычный нам знак «$parallel$, а знак равенства стали использовать для обозначения равенства чисел и выражений.

Видео:Параллельные и перпендикулярные прямые. 5 классСкачать

Параллельные прямые в жизни

Зачастую мы не замечаем, что в обычной жизни нас окружает огромное число параллельных прямых. Например, в нотной тетради и сборнике песен с нотами нотный стан выполнен с помощью параллельных линий. Также параллельные линии встречаются и в музыкальных инструментах (например, струны арфы, гитары, клавиши фортепиано и т.п.).

Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно. Рельсы линий метро и железных дорог располагаются параллельно.

Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий.

Видео:Математика 6 класс: Параллельные и перпендикулярные прямыеСкачать

Параллельные прямые в архитектуре

На представленных изображениях архитектурные сооружения содержат параллельные прямые. Использование параллельности прямых в строительстве помогает увеличить срок службы таких сооружений и придает им необычайную красоту, привлекательность и величие. Линии электропередач также умышленно проводятся параллельно, чтобы избежать их пересечения или соприкосновения, что привело бы к замыканию, перебоям и отсутствию электричества. Чтобы поезд мог беспрепятственно перемещаться рельсы также выполнены параллельными линиями.

В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.

Видео:Перпендикулярные прямые. 6 класс.Скачать

Проект по теме: Параллельные прямые в жизни

Видео:Перпендикулярные и параллельные прямые. Математика 6 классСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

I . Теоретическая часть

1.1. Определение параллельных прямых . . 4

1.2. Параллельные прямые в жизни . 4

1.3. Иллюзии параллельных прямых . 5

1.4.Способы построения параллельных прямых . 6

1.5.Профессиональные способы построения параллельных прямых …………7

1.6.Применение параллельных прямых в геометрии …………………………..7

II . Практическая часть

2.1. Анкетирование учащихся. 9

2.2. Изготовление проектного продукта…………… . 9

Список литературы . 11

Каждый современный ученик должен быть всесторонне развитым, поэтому ему необходимо владеть не только математическими знаниями, но и знать историю математики . Школьная программа , к сожалению, не предусматривает изучение вопроса «История параллельных прямых», а способы построения параллельных прямых изучаются не в полном объёме. Исходя из этого, я решила расширить свои знания в области математики, а именно: изучить историю параллельных прямых, показать их значимость и закрепить умения строить параллельные прямые на линованной и нелинованной бумаге. Поэтому выбранная мной тема исследования актуальна.

Гипотеза: Без параллельных прямых невозможна наша жизнь.

Цель моего проекта: Показать необходимость и значимость параллельных прямых.

1. Собрать материал по теме, изучив литературу и Интернет-источники.

2. Изучить определения, способы построения и применение параллельных прямых в жизни .

3. Провести анкетирование обучающихся школы.

4. Составить буклет “ Параллельные прямые в жизни”.

1.1. Определение параллельных прямых

С греческого языка понятие «параллелос» переводится «рядом идущий» или «проведенный друг возле друга». Этот термин использовался в древней школе Пифагора еще до того, как параллельные прямые получили свое определение.

В домашних справочных и энциклопедических изданиях я нашла несколько определений понятиям «параллель» и «параллельные прямые». Например, в самом популярном толковом словаре русского языка С. И. Ожегова и Н. Ю. Шведовой параллелью в математике называется «Прямая, не пересекающаяся другой прямой, лежащей с ней в одной плоскости».

А из занимательного толкового словаря В. И. Даля – “ПАРАЛЛЕЛЬ” ж. — параллельная линия, равна во всех точках от другой отстоящая и потому никогда не могущая с нею встретиться.

В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются. В другом варианте определения, совпадающие прямые также считаются параллельными (Приложение 4, рис. 27)

Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида . Отказ от пятого постулата ведёт к геометрии Лобачевского (Приложение 8).

В геометрии Лобачевского вместо неё принимается следующая аксиома: Через точку, не лежащую на данной прямой, проходят, по крайней мере, две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её (Приложение 4, рис. 25; рис. 26).

Согласно историческим фактам Евклидом в III в. До н.э. в его трудах все же был раскрыт смысл понятия параллельных прямых (Приложение 4, рис. 1).

В древности знак для обозначения параллельных прямых имел отличный вид того, что мы используем в современной математике. Например, древнегреческим математиком Паппом в III в. Н.э. параллельность обозначалась с помощью знака равенства. Т.е. тот факт, что прямая l параллельна прямой m ранее обозначался «l=m». Позднее для обозначения параллельности прямых стали использовать привычный нам знак « ∥» , а знак равенства стали использовать для обозначения равенства чисел и выражений.

1.2. Параллельные прямые в жизни

Зачастую мы не замечаем, что в обычной жизни нас окружает огромное число параллельных прямых. Например, в нотной тетради и сборнике песен с нотами нотный стан выполнен с помощью параллельных линий (Приложение 4, рис. 2). Также параллельные линии встречаются и в музыкальных инструментах (например, струны арфы, гитары, клавиши фортепиано и т.п.) (Приложение 4, рис. 3). Электрические провода, которые расположены вдоль улиц и дорог, также проходят параллельно (Приложение 4, рис. 4). Рельсы линий метро и железных дорог располагаются параллельно. Кроме быта параллельные линии можно встретить в живописи, в архитектуре, при строительстве зданий (Приложение 4, рис. 5; рис. 6 ; рис. 7).

На представленных изображениях архитектурные сооружения содержат параллельные прямые. Использование параллельности прямых в строительстве помогает увеличить срок службы таких сооружений и придает им необычайную красоту, привлекательность и величие. Линии электропередач также умышленно проводятся параллельно, чтобы избежать их пересечения или соприкосновения, что привело бы к замыканию, перебоям и отсутствию электричества. Чтобы поезд мог беспрепятственно перемещаться, рельсы также выполнены параллельными линиями. В живописи параллельные линии изображают сводящимися в одну линию или близкими к тому. Такой прием называется перспективой, которая следует из-за иллюзии зрения. Если долго смотреть вдаль, то параллельные прямые будут похожи на две сходящиеся линии.

1.3.Иллюзии параллельных прямых

Слово «иллюзия» происходит от латинского illusere – обманывать.

Зрительная иллюзия – ошибка в зрительном восприятии, искажение пространственных соотношений признаков воспринимаемых объектов, ошибка в оценке и сравнении между собой длин отрезков, величин углов, расстояний между предметами, в восприятии формы предметов, совершаемые наблюдателем при определенных условиях.

Начало изучению зрительных иллюзий положило обнаружение немецким астрофизиком Ф. Цёлльнером (1860 г.) в рисунке купленной ткани эффекта визуального схождения и расхождения вертикальных параллельных линий при пересечении их короткими косыми линиями. Эта иллюзия наиболее сильно проявляется, когда пересекающееся линии образуют угол, равный 45° (Приложение 3, рис. 8).

На уроках геометрии, приступая к решению задачи, мы, как правило, первым делом строим чертёж, опираясь на свое зрительное восприятие. Но такой подход к решению задачи часто приводит к ошибочным выводам, а значит к неверному решению. Мы привыкли доверять собственному зрению, однако оно нередко обманывает нас, показывая то, чего в действительности не существует. В такие моменты мы сталкиваемся со зрительными иллюзиями — ошибками зрительного восприятия (Приложение 3, рис. 9; рис. 10; рис. 11).

В настоящее время люди не только поражаются обманам зрения и забавляются зрительными иллюзиями, но и сознательно используют их в своей практической деятельности. Иллюзии применяются в архитектуре, изобразительном, цирковом искусстве, кинематографии и даже в военном деле (Приложение 3, рис. 12; рис. 13; рис. 14).

Но с другой стороны мы столкнулись со странным явлением: устремляя взгляд далеко в бесконечность, можно увидеть пересечение параллельных прямых!

В чем же дело? Чтобы ответить на этот вопрос обратимся к великим ученым.

Но сначала я обратилась к учащимся 7 Б класса. С ними провела эксперимент «Иллюзии зрения». Учащимся задали вопрос: везде ли на картинках параллельные прямые? Результаты опроса таковы: участвовали 20 человек из них: 7 – 35% считают параллельно, 13 -65% нет (Приложение 3).

Вывод: в геометрии истинность каждого утверждения необходимо доказывать, нельзя полагаться только на наблюдения.

Положительный момент: благодаря зрительным искажениям существует живопись.

1.4. Способы построения двух параллельных прямых

Изучив теоретические сведения, касающиеся параллельных прямых, возникла необходимость к изучению практических способов геометрических построений параллельных прямых на плоскости. Рассмотрим некоторые из них (Приложение 7):

🎥 Видео

Параллельные прямые. 6 класс.Скачать

ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕСкачать

Как провести множество параллельных или перпендикулярных прямых без транспортира?Скачать

10 класс, 15 урок, Перпендикулярные прямые в пространствеСкачать

Перпендикулярные прямыеСкачать

Математика 5 класс Параллельные и перпендикулярные прямыеСкачать

Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

Параллельные и перпендикулярные прямыеСкачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Перпендикулярные и параллельные прямыеСкачать

Введение в параллельные и перпендикулярные прямые (видео 59) | Подобие. Геометрия | МатематикаСкачать

Параллельные и перпендикулярные прямые. 6 классСкачать