Доказательства третий признак равенства треугольника (2 видео)

Третий признак равенства треугольников формулировка и доказательство

Третий признак равенства треугольников и его доказательство (всех трех возможных случаев) будут подробно рассмотрены в данной статье.

Содержание

Формулировка третьего признака равенства треугольников
Доказательство
Доказательство
Три возможных случая при наложении треугольников
Доказательства равенства треугольников для трех возможных случаев
Первый случай
Доказательство:
Второй случай
Доказательство:
Третий случай
Доказательство:
Признаки равенства треугольников
Первый признак равенства треугольников
Второй признак равенства треугольников
Третий признак равенства треугольников
3 признак равенства треугольников
🔍 Видео

Видео:Третий признак равенства треугольников | Теорема + доказательствоСкачать

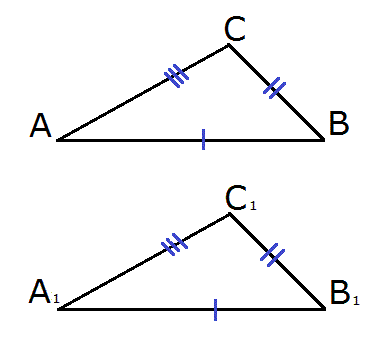
Формулировка третьего признака равенства треугольников

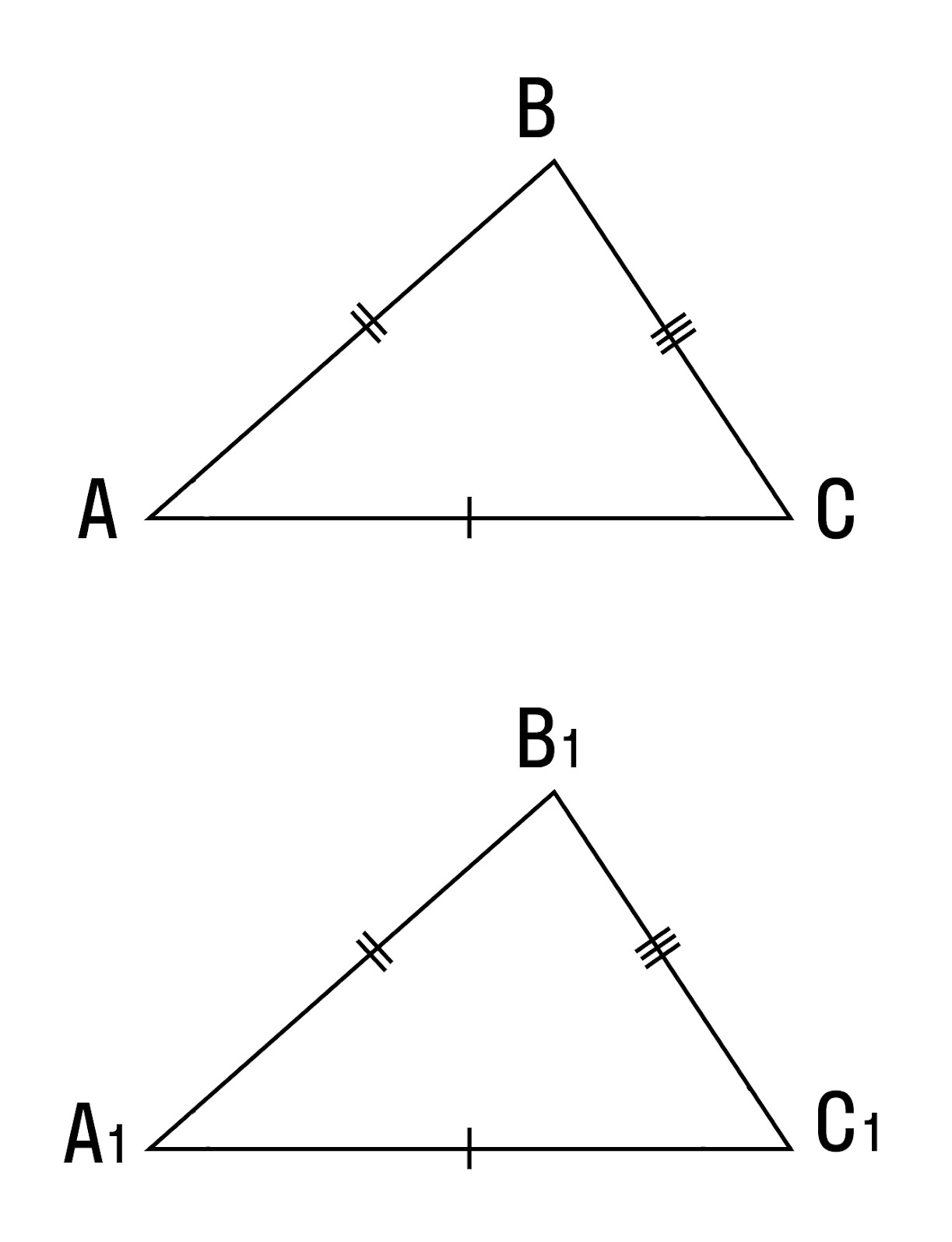
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Доказательство

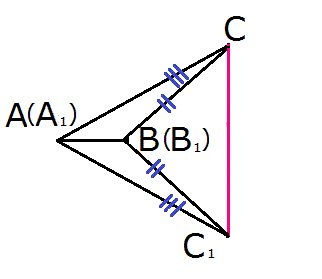
Требуется доказать, что треугольники АСВ и А₁В₁С₁ равны.

Доказательство

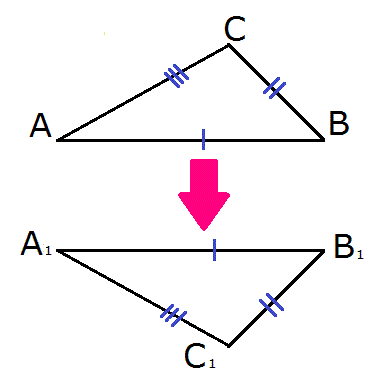
Для начала необходимо «наложить» данные треугольники друг на друга таким образом – чтобы точка А совпала с точкой А₁, точка В с точкой В₁, а точки С и С₁ оказались по разные стороны от прямой А₁В₁.

Три возможных случая при наложении треугольников

Луч С₁С расположен внутри угла А₁С₁В₁.

Луч С₁С накладывается на одну из сторон данного угла.

Видео:Третий признак равенства треугольников (доказательство) - геометрия 7 классСкачать

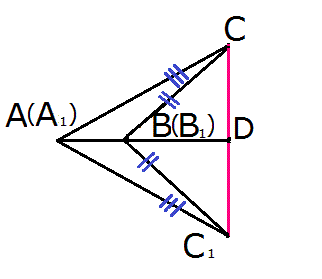
Доказательства равенства треугольников для трех возможных случаев

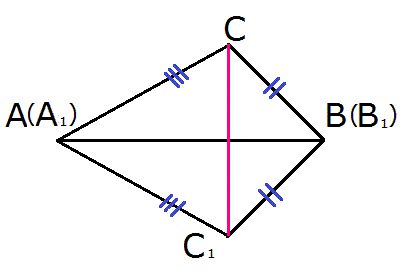
Первый случай

Доказательство:

Рассмотрим треугольники В₁С₁С и АС₁С.

По условию стороны АС=А₁С₁, ВС=В₁С₁, следовательно, треугольники В₁С₁С и А₁С₁С – равнобедренные.

Вспомнив, что углы при основании равнобедренных треугольников равны (свойство равнобедренного треугольника), получаем:
∠АСС₁ = ∠А₁С₁С,
∠ВСС₁ = ∠В₁С₁С.

Поскольку
∠ACB = ∠ACC₁ + ∠BCC₁,
∠AC1B = ∠AC₁C + ∠BC₁C,
то и углы AСB и AС₁B равны.

Так как ВС = В₁С₁, АС = А₁С₁ и ∠AСB = ∠AС₁B, можно утверждать, что треугольники АВС и А₁В₁С₁ равны согласно первому признаку равенства треугольников (по двум сторонам и углу между ними).

Что и требовалось доказать

Второй случай

Луч С₁С накладывается на одну из сторон этого угла.

Доказательство:

Рассмотрим треугольник САС₁.

Согласно условию теоремы, в треугольнике САС₁ стороны АС и А₁С₁ равны, следовательно, сам треугольник САС₁ — равнобедренный.

По аналогии с доказательством первого случая (пункты 3-5): так как треугольник САС₁ равнобедренный, то углы при его основании (СС₁) равны, то есть ∠С = ∠С₁ . Отсюда следует, что треугольники АВС и А₁В₁С₁ равны по двум сторонам и углу между ними.

Что и требовалось доказать.

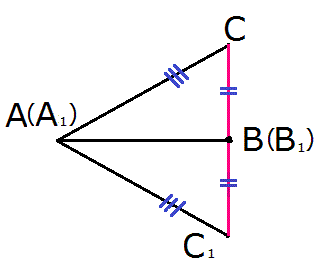
Третий случай

Доказательство:

Рассмотрим полученный треугольник ВСС₁.

По условию, стороны В₁С₁ и ВС – равны, следовательно, треугольник В₁С₁С – равнобедренный, а значит, что углы BСD и BС₁D равны.

Рассмотрим треугольник АСС₁.

Согласно условию, стороны АС и А₁С₁ – равны, отсюда следует, что треугольник АСС₁ – равнобедренный и углы при его основании равны (∠DC₁A = ∠DCA).

∠DCA = ∠DCB + ∠ACB, а ∠DC₁A = ∠DC₁B + ∠AC₁B.

Поскольку ∠DC₁A = ∠DCA и ∠BСD = ∠BС₁D, то отсюда следует, что и углы ∠АСВ и ∠АС₁В равны.

Исходя из вышенаписанного можно сделать вывод, что треугольники АВС и А₁В₁С₁ равны по двум сторонам и углу между ними.

Что и требовалось доказать.

Понравилась статья, расскажите о ней друзьям:

Видео:Признаки равенства треугольников. 7 класс.Скачать

Признаки равенства треугольников

О чем эта статья:

Видео:Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:Геометрия. 7 класс. Теоремы. Т8. Третий признак равенства треугольников.Скачать

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:7 класс, 20 урок, Третий признак равенства треугольниковСкачать

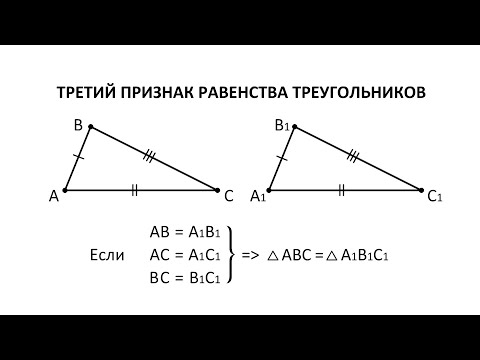
Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

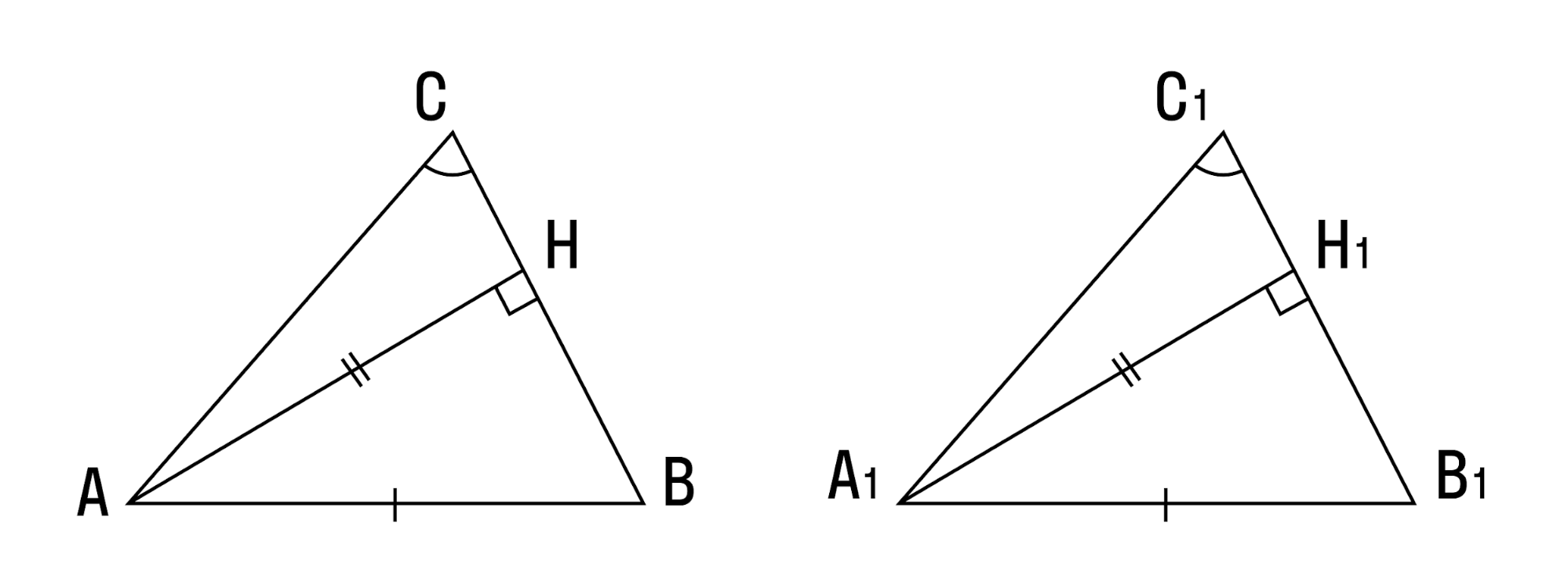
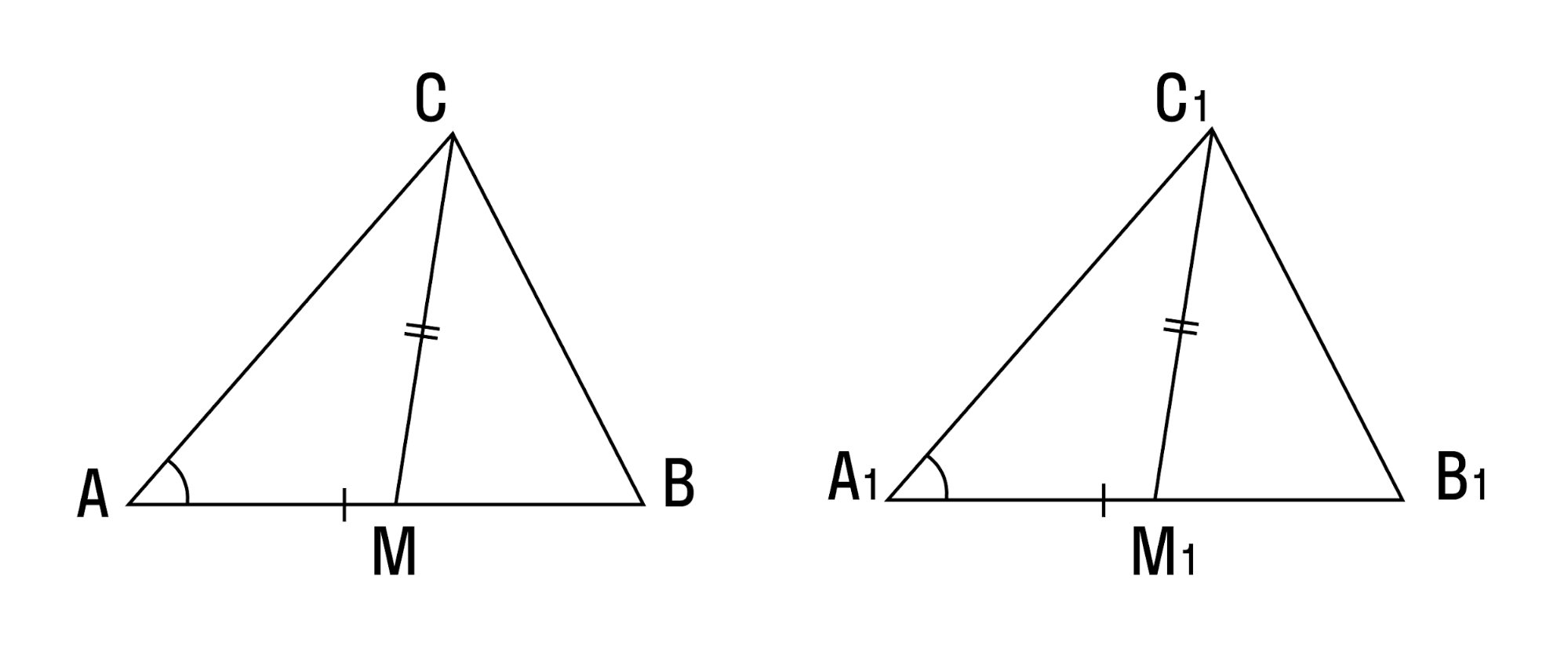
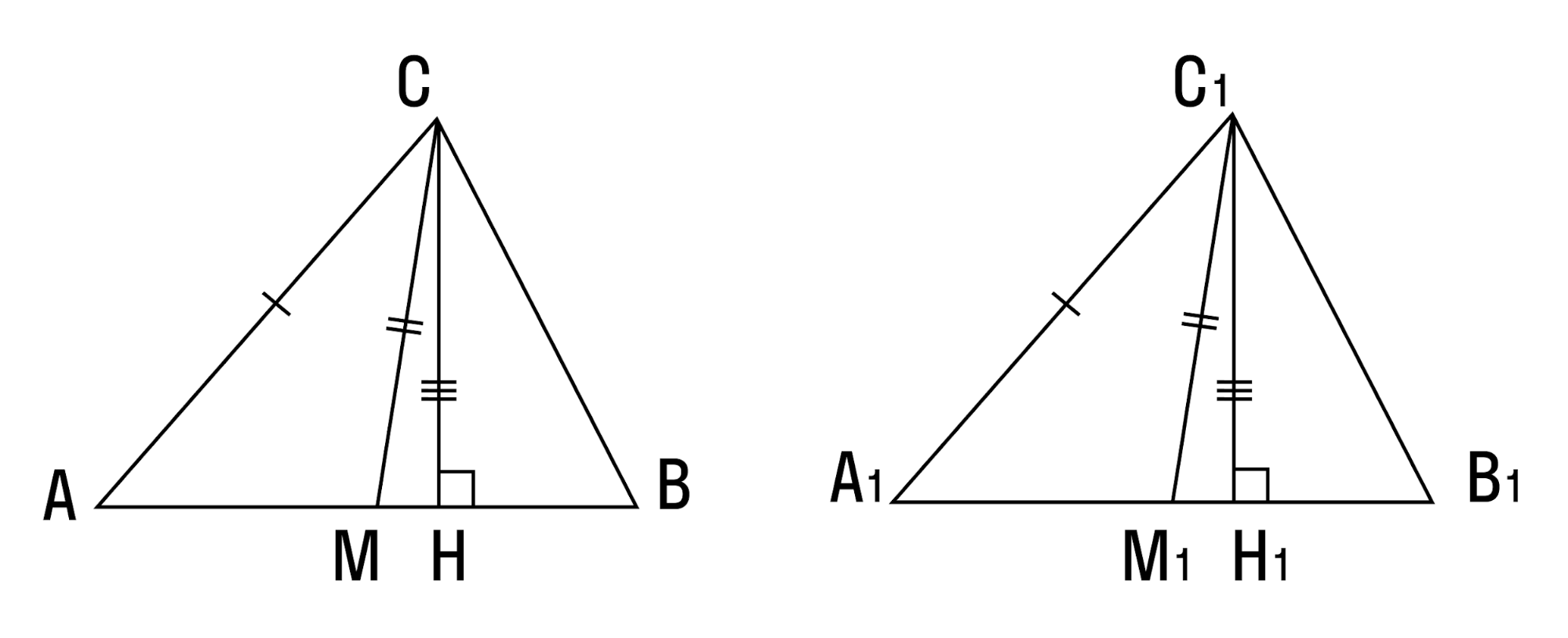
Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
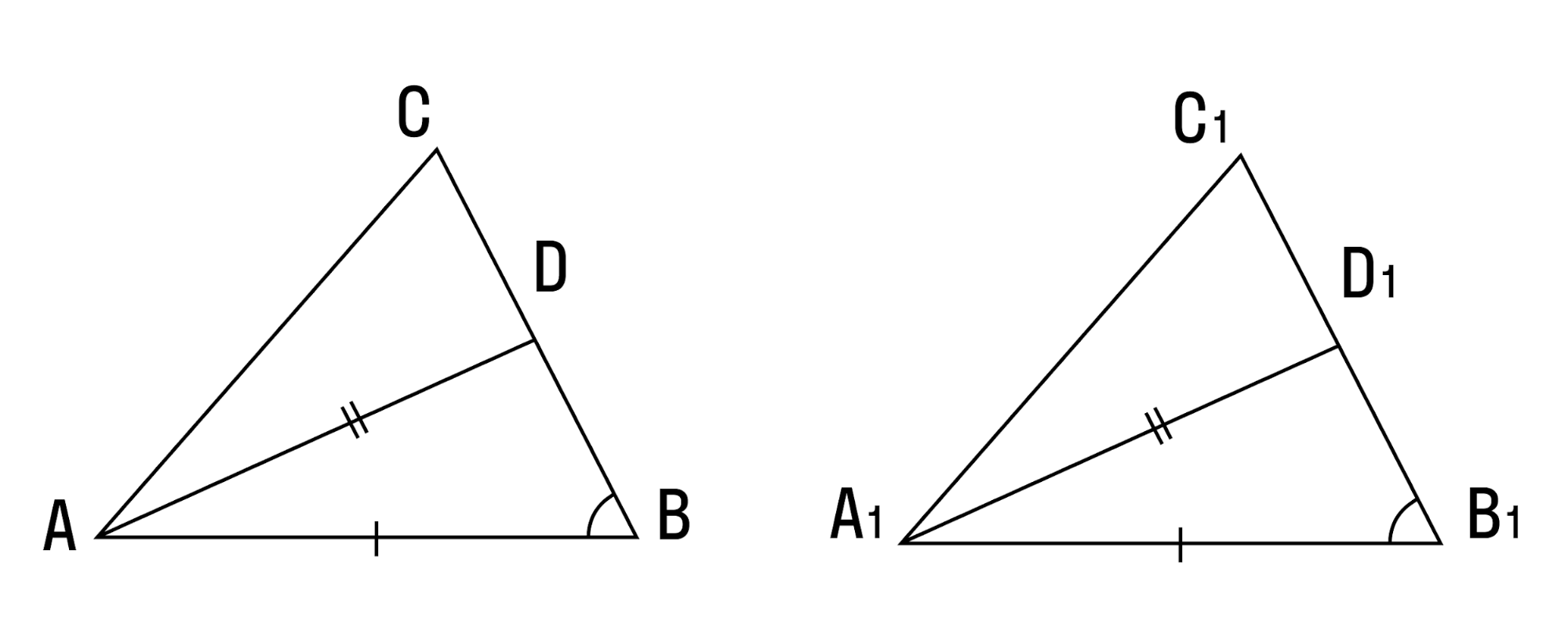
Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Видео:Третий признак равенства треугольников. ДоказательствоСкачать