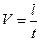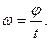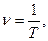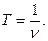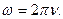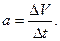Угловое движение можно условно разделить на два вида:
- Когда изменяется только направление вектора линейной скорости, а его длина не изменяется.
- Или, когда изменяются обе характеристики вектора линейной скорости.
Во втором случае, для описания движения будем применять более сложные формулы кинематики. Так как появится еще один вид ускорения.
Центростремительное (нормальное) ускорение есть всегда, когда есть движение по окружности, при этом не важно, меняется ли скорость тела по модулю, или не меняется.
- Движение по окружности с постоянной по модулю скоростью
- Тангенциальное ускорение – когда модуль скорости меняется
- Равноускоренное движение по окружности
- Равнозамедленное движение по окружности
- Общее ускорение при движении по окружности
- Движение по окружности
- Угловая скорость
- Нормальное ускорение
- Тангенциальное ускорение
- Движение по окружности.
- 🔍 Видео
Видео:Ускорение при равномерном движении по окружностиСкачать

Движение по окружности с постоянной по модулю скоростью
Пусть тело движется по окружности, но при этом длина вектора линейной скорости не меняется (рис. 1).
[left|vec right| = const]
На рисунке 1 указаны: а) – вид сбоку, б) вид сверху, вектор угловой скорости направлен к нам перпендикулярно рисунку.
Скорость будет меняться только по направлению от точки к точке, потому, что на тело действует центростремительная сила (displaystyle vec<F_<text>>) , тело обладает центростремительным (displaystyle vec<a_<text>>) (нормальным) ускорением.
Кроме линейной, тело обладает угловой скоростью. Если линейная скорость не изменяется по модулю, то длина вектора угловой скорости не меняется.
На рисунке 1а изображен вектор угловой скорости (displaystyle vec), на рисунке 1б вектор угловой скорости направлен к нам перпендикулярно плоскости рисунка. Направление, в котором тело движется по окружности, указано синей стрелкой.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Тангенциальное ускорение – когда модуль скорости меняется
Тело может увеличивать или уменьшать свою скорость, когда движется по окружности.
В таком случае, дополнительно к нормальному ускорению возникает тангенциальное (displaystyle vec<a_>) ускорение.
Тангенциальное ускорение играет роль линейного ускорения при прямолинейном движении тела. Вектор (displaystyle vec<a_>) направлен параллельно вектору (displaystyle vec) скорости.
Подобно движению по прямой, вектор ускорения – это первая производная скорости по времени, или вторая производная перемещения по времени.
Когда векторы скорости (vec) и ускорения (vec<a_>) сонаправлены (рис. 2), линейная и угловая скорости возрастают.
А когда ускорение (vec<a_>) направлено противоположно (рис. 3) вектору скорости (vec), угловая и линейная скорости уменьшаются.
С линейной скоростью (vec) связана угловая (vec) скорость.
Из рисунков 2, 3 следует: когда появляется тангенциальное ускорение, меняется и угловая скорость. Значит, тангенциальное ускорение (vec<a_>) появляется совместно с угловым (vec) ускорением и между ними есть связь.
Связь между тангенциальным и угловым ускорением выглядит аналогично связи между линейной и угловой скоростью.
В векторном виде
В скалярном виде
[ large boxed < a_= beta cdot R >]
(displaystyle vec left( frac<text><c^>right)) – угловое ускорение;
(displaystyle vec< a_> left( frac<text><c^>right)) – тангенциальное ускорение;
(R left( textright)) – радиус окружности.
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Равноускоренное движение по окружности
Угловая скорость увеличивается (рис. 2), когда угловое ускорение сонаправлено с вектором угловой скорости. Когда движение происходит с постоянным ускорением, его называют равноускоренным.
Для решения задач на равноускоренное движение по окружности, поступаем аналогично равноускоренному движению по прямой. Применяем систему из двух уравнений:
[ large boxed < beginomega = omega _ + beta cdot t \ displaystyle varphi = omega_ cdot t + beta cdot frac end > ]
Первое уравнение системы – это связь между начальной (omega_ ) и конечной (omega ) скоростью. Второе уравнение – это уравнение движения.
Видео:Физика - движение по окружностиСкачать

Равнозамедленное движение по окружности
Когда векторы (vec) и (vec) направлены в противоположные стороны, угловая скорость (vec) уменьшается (рис. 3).
Для решения задач кинематики, в которых угловая скорость уменьшается и, движение равнозамедленное, используем систему, состоящую из таких уравнений:
[ large boxed < beginomega = omega _ — beta cdot t \ displaystyle varphi = omega_ cdot t — beta cdot frac end > ]
Видео:Центростремительное ускорение. 9 класс.Скачать

Общее ускорение при движении по окружности
Пусть точка движется по окружности и линейная (vec) скорость ее изменяется по модулю. При этом, точка обладает двумя видами ускорения — нормальным и тангенциальным. Эти виды ускорения обозначают символом (vec).
Примечание: Любое ускорение, обозначаемое символом «a», измеряется в метрах, деленных на секунду в квадрате.
Направление вектора общего ускорения указано на рисунке 4а, а для равнозамедленного – на рисунке 4б.
Так как векторы (vec<a_>) и (vec<a_>) всегда перпендикулярны, длину вектора общего ускорения (vec) можно найти из теоремы Пифагора:
Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Движение по окружности.
1.Равномерное движение по окружности
2.Угловая скорость вращательного движения.
5.Связь линейной скорости с угловой.
7.Равнопеременное движение по окружности.
8.Угловое ускорение в равнопеременном движении по окружности.
10.Закон равноускоренного движения по окружности.
11. Средняя угловая скорость в равноускоренном движении по окружности.
12.Формулы, устанавливающие связь между угловой скоростью, угловым ускорением и углом поворота в равноускоренном движении по окружности.
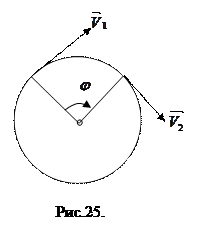
и называется линейной скоростью движения по окружности.
Как и в криволинейном движении вектор скорости направлен по касательной к окружности в направлении движения (Рис.25).
2. Угловая скорость в равномерном движении по окружности – отношение угла поворота радиуса ко времени поворота:
В равномерном движении по окружности угловая скорость постоянна. В системе СИ угловая скорость измеряется в(рад/c). Один радиан – рад это центральный угол, стягивающий дугу окружности длиной равной радиусу. Полный угол содержит 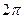
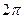
3. Период вращения – интервал времени Т, в течении которого материальная точка совершает один полный оборот. В системе СИ период измеряется в секундах.
4. Частота вращения – число оборотов 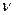
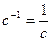
Если за время t точка совершает n оборотов по окружности то 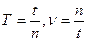
Зная период и частоту вращения, угловую скорость можно вычислять по формуле:
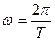
5 Связь линейной скорости с угловой. Длина дуги окружности равна 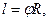
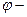
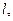
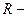
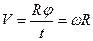
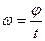
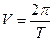
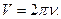
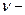
6. Центростремительное ускорение. В равномерном движении по окружности модуль скорости остаётся неизменным 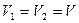
Пусть за промежуток времени 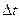
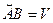
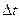
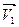
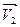
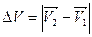
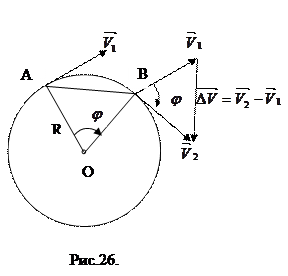
На Рис.26 треугольники АОВ и ДВС равнобедренные и углы при вершинах О и В равны, как углы с взаимно перпендикулярными сторонами АО 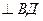
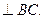
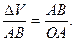
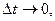
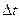
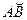
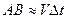
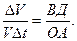
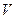
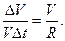
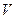
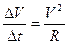
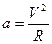

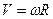
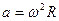
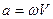
Итак, в равномерном движении по окружности центростремительное ускорение постоянно по модулю.
Легко сообразить, что в пределе при 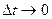
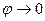
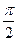
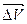
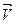
7. Равнопеременное движение по окружности – движение по окружности, при котором за равные интервалы времени угловая скорость изменяется на одну и ту же величину.
8. Угловое ускорение в равнопеременном движении по окружности – отношение изменения угловой скорости к интервалу времени 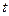
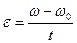
где 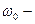
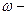
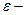
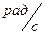
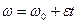
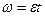
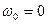
Умножая обе части этих равенств на 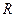
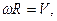
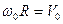
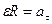
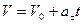
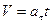
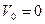
9. Тангенциальное ускорение численно равно изменению скорости в единицу времени и направлено вдоль касательной к окружности. Если 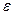
Дата добавления: 2015-08-08 ; просмотров: 17306 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🔍 Видео
Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Ускорение при криволинейном движенииСкачать

Скорость и ускорение при равномерном движении по окружности. Видеоурок 6. Физика 9 классСкачать

Линейная и угловая скорости при равномерном движении по окружностиСкачать

Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

"Скорость при движении по окружности".Скачать

Физика | Равномерное движение по окружностиСкачать

7-класс | Физика | Ускоренное и замедленное движение. Движение по окружностиСкачать

ЦЕНТРОСТРЕМИТЕЛЬНОЕ УСКОРЕНИЕ кинематика 9 и 10 классСкачать