Взаимно перпендикулярные стороны треугольника (2 видео)

Please wait.

Содержание

We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
Взаимно перпендикулярные стороны треугольника
Теорема об углах с соответственно перпендикулярными сторонами
🌟 Видео

Видео:Перпендикулярные прямые. 6 класс.Скачать

We are checking your browser. mathvox.ru

Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d307cb938d616f0 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:Перпендикулярные прямыеСкачать

Взаимно перпендикулярные стороны треугольника

Ключевые слова: треугольник, прямоугольный, катет, гипотенуза, теорема Пифагора, окружность

Треугольник называют прямоугольным, если у него есть прямой угол.
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой.

По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
Сумма двух острых углов прямоугольного треугольника равна прямому углу.
Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.
Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СD = h_c из вершины С его прямого угла.

Она разобьет данный треугольник на два прямоугольных треугольника АСD и ВСD; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС.

Все три треугольника АВС, АСD и ВСD подобны между собой.

Взаимно перпендикулярные стороны треугольника

Из подобия треугольников определяются соотношения:

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.

Геометрическая формулировка. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Алгебраическая формулировка. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
a 2 + b 2 = c 2

Обратная теорема Пифагора. Для всякой тройки положительных чисел a, b и c, такой, что
a 2 + b 2 = c 2 ,
существует прямоугольный треугольник с катетами a и b и гипотенузой c.

Признаки равенства прямоугольных треугольников:

по катету и гипотенузе;
по двум катетам;
по катету и острому углу;
по гипотенузе и острому углу.

См. также:
Площадь треугольника, Равнобедренный треугольник, Равносторонний треугольник

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Теорема об углах с соответственно перпендикулярными сторонами

Теорема

Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют 180 0 .

Дано: АОВ, А₁О₁В₁, ОАО₁А₁, ОВО₁В₁.

Доказать: АОВ = А₁О₁В₁ или АОВ + А₁О₁В₁ = 180 0 .

Доказательство:

1 случай

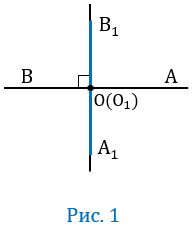
Пусть угол АОВ — развернутый (Рис. 1).

Угол АОВ — развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОАО₁А₁, ОВО₁В₁, значит, лучи О₁А₁ и О₁В₁ также будут лежать на одной прямой, следовательно, А₁О₁В₁ — будет развернутым, тогда АОВ = А₁О₁В₁.

2 случай

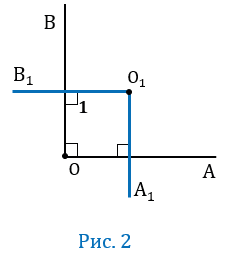
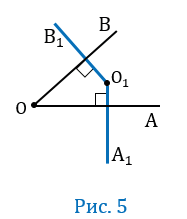
Пусть угол АОВ — прямой, т.е. равен 90 0 (Рис.2).

АОВ = 90 0 , то ОАОВ, при этом по условию ОАО₁А₁, следовательно, ОВО₁А₁. Итак, О₁В₁ — секущая относительно прямых ОВ и О₁А₁, ОВО₁А₁, тогда по теореме об односторонних углах их сумма равна 180 0 , т.е. 1 + А₁О₁В₁ = 180 0 , откуда А₁О₁В₁ = 180 0 —1, при этом по условию ОВО₁В₁, значит 1 — прямой, т.е. 1 = 90 0 , следовательно, А₁О₁В₁ = 180 0 — 90 0 = 90 0 . Из равенств АОВ = 90 0 и А₁О₁В₁ = 90 0 следует, что АОВ = А₁О₁В₁ и АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

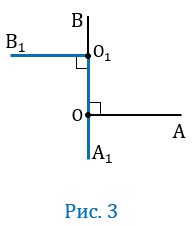
3 случай

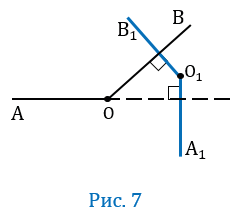
Пусть ОО₁А₁ (Рис.3).

По условию ОО₁А₁, тогда лучи ОВ и О₁А₁ будут лежать на одной прямой А₁В. По условию ОАО₁А₁, ОВО₁В₁, значит, ОА и О₁В₁ будут перпендикулярны одной прямой А₁В, следовательно, ОАО₁В₁. Итак, ОАО₁В₁, А₁В — секущая относительно прямых ОА и О₁В₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

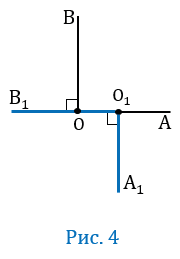
4 случай

Пусть ОО₁В₁ (Рис.4).

По условию ОО₁В₁, тогда лучи ОА и О₁В₁ будут лежать на одной прямой В₁А. По условию ОАО₁А₁, ОВО₁В₁, значит ОВ и О₁А₁ будут перпендикулярны одной прямой В₁А, следовательно, ОВО₁А₁. Итак, ОВО₁А₁, В₁А — секущая относительно прямых ОВ и О₁А₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

5 случай

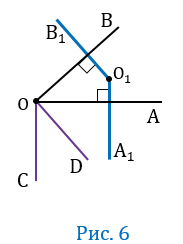
Пусть угол АОВ — острый, т.е. меньше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.5).

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОАОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).

Получим, что АОВ = 90 0 — АОD, а СОD = 90 0 — АОD, значит АОВ = СОD. Стороны угла СОD соответственно параллельны сторонам угла А₁О₁В₁, т.е. ОСО₁А₁ (т.к. две прямые перпендикулярные к третьей прямой параллельны друг другу, по построению ОАОС и по условию ОАО₁А₁), также ОDО₁В₁ (т.к. по построению ОВОD и по условию ОВО₁В₁), поэтому по теореме об углах с соответственно параллельными сторонами либо СОD = А₁О₁В₁, либо СОD + А₁О₁В₁ = 180 0 . Следовательно, учитывая то, что АОВ = СОD получим, либо АОВ = А₁О₁В₁, либо АОВ + А₁О₁В₁ = 180 0 .

6 случай

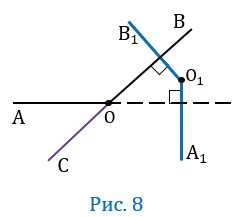
Пусть угол АОВ — тупой, т.е. меньше 180 0 , но больше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.7).

Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.8).

Угол АВС острый, и его стороны соответственно перпендикулярны сторонам угла А₁О₁В₁. Следовательно, либо АОС + А₁О₁В₁ = 180 0 , либо АОС = А₁О₁В₁ (смотри случай 5). Тогда, учитывая, что углы АОС и АОВ смежные, их сумма будет равна 180 0 , значит АОС = 180 0 — АОВ, следовательно, в первом случае 180 0 — АОВ + А₁О₁В₁ = 180 0 , откуда АОВ = А₁О₁В₁, а во втором случае 180 0 — АОВ = А₁О₁В₁, откуда АОВ + А₁О₁В₁ = 180 0 . Что и требовалось доказать.