Через вершины треугольника проведена окружность

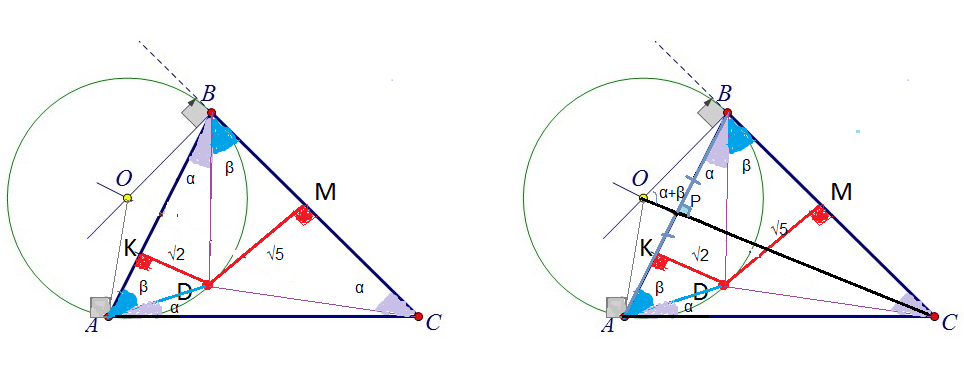
Условие

Через вершины А и В треугольника АВС проведена окружность, касающаяся прямых АС и ВС. На этой окружности выбрана точка D (внутри треугольника), лежащая на расстоянии sqrt(2) от прямой АВ и на расстоянии sqrt(5) от прямой ВС. Найдите угол DBC, если известно, что угол ABD = углу BCD.

Решение

Обозначим
∠ ABD= ∠ BCD = альфа
∠ ABD вписанный в окружность, опирается на дугу AD.
∠ ABD=(1/2) ∪ AD

∠ DAC =(1/2) ∪ AD как угол между касательной и хордой.

∠ ABD= ∠ BCD = ∠ DAC= альфа

Обозначим
∠ DВС = бета
Это угол между касательной ВС и хордой BD,
∠ DВC =(1/2) ∪ ВD .
∠ BАD вписанный в окружность, опирается на дугу ВD.
∠ BАD=(1/2) ∪ ВD
∠ DBC= ∠ BAD = бета

Из прямоугольного треугольника ВКD
KB=sqrt(2) ctg альфа
Из прямоугольного треугольника AКD
AK=sqrt(2) ctg бета
AB=AK+KB=sqrt(2)*(ctg альфа +ctg бета)

[b]AB=sqrt(2)*(ctg альфа +ctg бета)[/b]

Аналогично.
Из прямоугольного треугольника ВМD
BМ=sqrt(5) ctg бета
Из прямоугольного треугольника СМD
СМ=sqrt(5) ctg альфа
BС=ВМ+МС=sqrt(5)*(ctg альфа +ctg бета)

[b]BС=sqrt(5)*(ctg альфа +ctg бета)[/b]

Δ BDC подобен Δ ABD по двум углам.
Из подобия
[b]ВС:АВ=BD:AD[/b]

По теореме синусов:
BD:sin бета =AD:sin альфа ⇒
[b] BD:AD=sin бета : sin альфа [/b]

и
из ВС:АВ=BD:AD получаем
[b] sin бета : sin альфа =sqrt(5):sqrt(2) [/b]

Δ АВС — равнобедренный (ВС=АС по свойству касательных к окружности, проведенных из одной точки С).

ΔАОВ — равнобедренный (ОА=ОВ=R)
CO ⊥ AB
BP=PA
В равнобедренном треугольнике высота СР является одновременно и медианой и биссектрисой.

Δ ОВР — прямоугольный ( ∠ OBC= 90 градусов, значит
∠ ОВР=90 градусов — альфа — бета, ∠ BOP= альфа + бета)

Из прямоугольного треугольника ВРС
ВР=ВС*cos( альфа + бета )
ВР=1/2 АB

АB=2ВС*cos( альфа + бета )
sqrt(2)*(ctg альфа +ctg бета)=2sqrt(5)*(ctg альфа +ctg бета)*cos( альфа + бета ) ⇒

[b] cos( альфа + бета)=(sqrt(10))/10 [/b] ⇒

Планиметрия закончилась.
Тригонометрия:

Обозначим.
sin бета = x, тогда сos бета = sqrt(1-x^2).
sin альфа=sqrt((2/5))x и cos альфа=sqrt(1-(2/5)x^2)

Так как
cos( альфа + бета)=cos альфа * cos бета — sin альфа * sin бета, то

Возводим обе части уравнения в квадрат.

sin бета = sqrt(2)/2

бета = 45 градусов.

О т в е т. 45 градусов.

Видео:Вершины треугольника делят окружность на три дуги, длины которых относятся как 3:4:11Скачать

Через вершины треугольника проведена окружность

Через вершины B и C треугольника ABC проходит окружность, пересекающая стороны AB и AC соответственно в точках K и M.

а) Доказать, что треугольники ABC и AMK подобны.

б) Найти MK и AM, если AB = 2, BC = 4, CA = 5, AK = 1.

а) Из свойств секущих к окружности известно:

Получаем, что треугольники ABC и AMK подобны (так как угол A — общий). Что и требовалось доказать.

б) Из подобия треугольников имеем:

Подставляя сюда известные значения, получим:

Ответ:

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б.	3
Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки.	2
Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:Через вершины А и В треугольника АВС проведена окружность, касающаяся прямыхСкачать Через вершины А и В треугольника АВС проведена окружность, пересекающая стороны АС и ВС в точках D и Е соответственно. Докажите Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать Ваш ответ Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать Похожие вопросы Все категории экономические 43,277 гуманитарные 33,618 юридические 17,900 школьный раздел 606,845 разное 16,824 Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 🎬 Видео Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать Всё про углы в окружности. Геометрия | МатематикаСкачать Вершины треугольника делят окружность на три дуги, длины которых относятся как 6:13:17Скачать 8 Расстояние от вершины треугольника до точек касания вписанной окружности со сторонамиСкачать Геометрия Вершины треугольника делят описанную около него окружность на три дуги, длины которыхСкачать Геометрия Вершины треугольника соединены с центром вписанной в него окружности Проведенные отрезкиСкачать №665. Вершины треугольника ABC лежат на окружности. Докажите, что если АВ — диаметр окружностиСкачать Изогонали угла. Радиус описанной окружности и высота, проведенные из одной вершины треугольника.Скачать ОГЭ 2021. Задание 24. Геометрическая задача на вычисление.Скачать ✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать Геометрия. 7 класс. Урок 9 "Окружность проходящая через вершины треугольника"Скачать №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать №205. Через вершину С прямого угла прямоугольного треугольника ABC проведена прямая CD, перпендикуляСкачать Высота, биссектриса, медиана. 7 класс.Скачать Как найти расстояние от вершины треугольника до ортоцентра? Профиматика и ЕГЭматика знают ответ!Скачать Геометрия. Задача. Треугольник. Окружность.Скачать 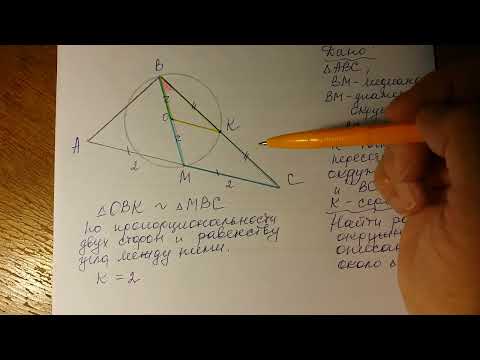Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности