Теорема о пересекающихся прямых соответственно параллельные перпендикулярным прямым (4 видео)

Теорема о пересекающихся прямых соответственно параллельные перпендикулярным прямым

Перпендикулярность прямых в пространстве

Так же как и на плоскости, две прямые называются перпендикулярными, если они пересекаются под прямым углом.

Теорема 17.1. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.

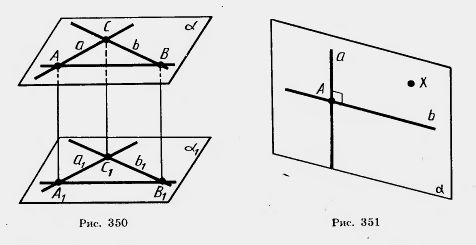
Доказательство. Пусть а и b — перпендикулярные прямые, а₁ и b₁ — параллельные им пересекающиеся прямые.

Докажем, что прямые а₁ и b₁перпендикулярны.

Если прямые а, b, а₁, b₁ лежат в одной плоскости, то они обладают указанным в теореме свойством, как это известно из планиметрии.

Допустим теперь, что наши прямые не лежат в одной плоскости. Тогда прямые а и b лежат в некоторой плоскости , а прямые а₁ и b₁ — в некоторой плоскости 1 (рис. 350). По теореме 16.4 плоскости и ₁ параллельны.. Пусть С — точка пересечения прямых а и b, а C₁ — точка пересечения прямых

а₁ и b₁. Проведем в плоскости параллельных прямых и ₁ прямую, параллельную прямой СС₁. Она пересечет прямые а и а₁ в точках А и А₁.B плоскости прямых b и b₁ проведем прямую, параллельную прямой СС₁, и обозначим через В и В₁ точки ее пересечения с прямыми b и b₁.

Четырехугольники САА₁С₁и СВВ₁С₁ — параллелограммы, так как у них противолежащие стороны параллельны. Четырехугольник АВВ₁ А₁ также параллелограмм. У него стороны АА₁, ВВ₁ параллельны, потому что каждая из них параллельна прямой CC₁. Таким образом, четырехугольник лежит в плоскости, проходящей через параллельные прямые АА₁ и ВВ₁. А она пересекает параллельные плоскости и ₁ по параллельным прямым АВ и А₁В₁.

Так как у параллелограмма противолежащие стороны равны, то АВ = А₁В₁, AC=А₁C₁, BC = B₁C₁. По третьему признаку равенства треугольников треугольники ABC и А₁В₁C₁ равны. Итак, угол А₁C₁B₁, равный углу АСВ, прямой, т. е. прямые а₁ и b₁ перпендикулярны. Теорема доказана.

Задача (1). Докажите, что через любую точку прямой в пространстве можно провести перпендикулярную ей прямую.

Решение. Пусть a — прямая а А — точка на ней (рис. 351). Возьмем любую точку X вне прямой a и проведем через эту точку и прямую a плоскость (теорема 15.1). В плоскости через точку А можно провести прямую b, перпендикулярную прямой a.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Содержание

Стереометрия. Страница 3
1. Перпендикулярность прямых в пространстве
2.Признак перпендикулярности прямой и плоскости
3. Теорема о трех перпендикулярах
5. Расстояние между скрещивающимися прямыми
5. Пример 1
Пример 2
Пример 3
Пример 4
Пример 5
Теорема о пересекающихся прямых соответственно параллельные перпендикулярным прямым
💡 Видео

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Стереометрия. Страница 3

Главная
Репетиторы
Учебные материалы
Контакты

Видео:Перпендикулярные прямые. 6 класс.Скачать

1. Перпендикулярность прямых в пространстве

Теорема. Если две пересекающиеся прямые параллельны двум перпендикулярным прямым, то они перпендикулярны и между собой.

Доказательство. Пусть а и b две перпендикулярные прямые, а точка F — их точка пересечения (Рис.1). А а’ и b’ параллельны им и точка F’ — их точка пересечения. Необходимо доказать, что a’ и b’ перпендикулярны между собой.

Если все прямые лежат в одной плоскости, то согласно теоремам планиметрии они перпендикулярны. Предположим, что наши прямые не лежат в одной плоскости. Тогда проведем через прямые а и b плоскость α. А через прямые a’ и b’ плоскость β. Тогда по признаку параллельности плоскостей эти две плоскости параллельны. Проведем плоскость через параллельные прямые a и a’. А в этой плоскости прямую AA’, параллельную прямой FF’. Проведем также плоскость через прямые b и b’. А в этой плоскости прямую BB’, параллельную прямой FF’. Тогда получим два параллелограмма — AFF’A’ и BFF’B’. Так как прямые a и a’, b и b’ параллельны по условию, а прямые AA’, FF’, BB’ по построению. По свойству параллелограмма противолежащие стороны равны. А следовательно треугольники AFB и A’F’B’ равны по трем сторонам. Отсюда следует, что угол при вершине F’ прямой. Т.е. прямые a’ и b’ перпендикулярны.

5. Пример 1

Докажите, что через точку, не лежащую в данной плоскости, можно провести только одну прямую, перпендикулярную данной плоскости.

Доказательство:

Пусть дана плоскость α и точка А, не лежащая на данной плоскости. Проведем в плоскости α две пересекающиеся прямые d и c. А через их точку пересечения О проведем прямую f, перпендикулярную d и с (Рис.6).

Тогда по признаку перпендикулярности прямой и плоскости, прямая f будет перпендикулярна плоскости α. Теперь проведем прямую АВ, параллельную прямой f. Тогда АВ будет перпендикуляром к плоскости α также.

Докажем, что АВ — единственный перпендикуляр. Допустим, что существует два перпендикуляра АВ и АB’ к плоскости α, которые проходят через точку А. Тогда через две пересекающиеся прямые АВ и АB’ проведем плоскость β. Она будет пересекать плоскость α по прямой b.

Возьмем на прямой b произвольную точку С и проведем в плоскости β прямую а, перпендикулярную прямой b. Тогда согласно аксиоме, (через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной), прямая АВ, параллельная прямой а, единственная. Т.е. перпендикуляр АВ к прямой b. Таким образом, перпендикуляр АВ единственный.

Рис.6 Задача. Докажите, что через точку, не лежащую в данной плоскости.

Пример 2

Через точку А прямой а проведены перпендикулярные ей плоскость β и прямая b. Докажите, что прямая b лежит в плоскости β.

Доказательство:

Пусть дана прямая а, перпендикулярные ей плоскость β и прямая b. Плоскость β и прямая b проходят через точку А прямой а (Рис.7). Необходимо доказать, что прямая b принадлежит плоскости β.

Проведем через две пересекающиеся прямые а и b плоскость α. Тогда две плоскости α и β пересекаются по прямой b’. Так как точка А принадлежит обоим плоскостям, то она лежит на прямой b’.

Таким образом, получается, что через точку А проходят две прямые b и b’, которые принадлежат плоскости α. Плоскость β перпендикулярна прямой а по условию задачи. А следовательно, прямая а перпендикулярна прямой b’. Отсюда следует, что через точку А проходят две прямые, лежащие в одной плоскости α, и перпендикулярные прямой а. А это невозможно. Так как через точку прямой можно провести только одну перпендикулярную ей прямую. Следовательно, прямые b и b’ совпадают. А отсюда следует, что прямая b полностью принадлежит плоскости β.

Рис.7 Задача. Через точку А прямой а проведены перпендикулярные ей плоскость β.

Пример 3

Через центр описанной около треугольника окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от вершин треугольника.

Доказательство:

Пусть дан треугольник АВС и описанная вокруг него окружность с центром в точке О. Прямая а перпендикулярна плоскости треугольника (Рис.8). Необходимо доказать, что каждая точка прямой а равноудалена от вершин треугольника А, В и С.

Рассмотрим треугольник АВС. Вокруг него описана окружность с центром в точке О, поэтому отрезки АО, ВО и СО равны как радиусы. Теперь возьмем произвольную точку Х на прямой а. Так как прямая а перпендикулярна плоскости треугольника, то треугольники АОХ, ВОХ и СОХ равны по первому признаку равенства треугольников, т.е. по двум сторонам и углу между ними. У них сторона ОХ общая, а стороны АО, ВО и СО равны как радиусы. И углы между этими сторонами составляют 90°.

Отсюда можно сделать вывод, что стороны АХ, ВХ и СХ этих треугольников равны. Т.е. расстояние от вершин треугольника АВС до любой точки прямой а одинаковые.

Рис.8 Задача. Через центр описанной около треугольника окружности.

Пример 4

Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная его плоскости. Расстояние от точки К до других вершин прямоугольника равны 9 см, 13 см и 15 см. Найдите АК.

Решение:

Пусть дан прямоугольник АВСD и прямая АК, перпендикулярная плоскости прямоугольника. ВК = 9 см, СК = 15 см, DK = 13 см (Рис.9). Необходимо найти АК.

Так как прямая АК перпендикулярна плоскости прямоугольника, то она перпендикулярна прямым АВ, AD и АС. Отсюда следует, что по теореме Пифагора можно составить следующие соотношения:

АВ 2 + AK 2 = BK 2

АВ 2 + AD 2 + AK 2 = CK 2

АD 2 + AK 2 = DK 2

Решая первое и третье соотношение относительно АВ 2 , АD 2 и подставляя полученные выражения во второе, получим:

BK 2 — AK 2 + DK 2 — AK 2 + AK 2 = CK 2

AK 2 = BK 2 — CK 2 + DK 2

AK 2 = 9 2 — 15 2 + 13 2

AK 2 = 25 или АК = 5 см.

Рис.9 Задача. Через вершину А прямоугольника ABCD.

Пример 5

Через основание трапеции проведена плоскость, отстоящая от другого основания на расстоянии 2 см. Найдите расстояние от точки пересечения диагоналей трапеции до этой плоскости, если основания трапеции относятся как 4:5 (верхнее к нижнему).

Решение:

Пусть дана трапеция АВСD. Плоскость α проведена через основание AD (Рис.10). ВС / AD = 4 / 5. Необходимо найти OO’.

Рассмотрим треугольники ВОС и AOD. Они подобны по трем углам. Коэффициент подобия составляет 4 / 5. Отсюда следует, что высоты ОЕ и ОF также относятся как 4 / 5.

Теперь рассмотрим треугольники FOO’ и FEE’. Они также подобны по трем углам. Коэффициент подобия у них составляет 5 / 9.

Таким образом, OO’ = EE’ 5 / 9 = 2*5 / 9 = 10 / 9 см.

Рис.10 Задача. Через основание трапеции проведена плоскость.

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Теорема о пересекающихся прямых соответственно параллельные перпендикулярным прямым

Главная > Учебные материалы > Математика: Стереометрия. Страница 3


1.Перпендикулярность прямых в пространстве. 2.Признак перпендикулярности прямой и плоскости. 3.Теорема о трех перпендикулярах. 4.Признак перпендикулярности плоскостей. 5.Расстояние между скрещивающимися прямыми. 6.Примеры.

1 2 3 4 5 6 7 8

Теорема о пересекающихся прямых соответственно параллельные перпендикулярным прямым

Рис. 1 Перпендикулярность прямых в пространстве.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

2.Признак перпендикулярности прямой и плоскости

Теорема. Прямая, перпендикулярная двум пересекающимся прямым на плоскости, перпендикулярна данной плоскости.

Доказательство. Пусть прямые k и b две пересекающиеся прямые на плоскости α. Прямая а перпендикулярна прямым k и b. Доказать, что прямая а перпендикулярна плоскости α. (Рис.2)

Проведем произвольную прямую х от точки А и прямую АВ, которая пересечет прямые k и b в точках К и В на плоскости α. Отложим на прямой а два равных отрезка в разные стороны АА’ и AA». Тогда треугольники АА’K и AA»K будут равны по двум сторонам и углу между ними. Так же как и треугольники АА’В и AA»В. Отсюда следует, что треугольники А’BK и А»BK равны по третьему признаку равенства треугольников. И следовательно, треугольники А’BE и A»BE равны, т.к. одна сторона у них общая ВЕ, стороны А’B и А»B равны из предыдущих рассуждений. Углы между этими сторонами также равны. Следовательно мы приходим к выводу, что треугольники А’AE и A»AE равны по трем сторонам. АЕ является медианой, биссектрисой и высотой, так как стороны А’Е и A»Е у них равные. И следовательно, угол между сторонами АА’ и АЕ равен 90°. Это значит, что прямая а перпендикулярна плоскости α.

Рис.2 Признак перпендикулярности прямой и плоскости

Видео:Параллельные прямые. 6 класс.Скачать

3. Теорема о трех перпендикулярах

Теорема: если прямая, проведенная на плоскости и проходящая через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и наклонной.

Доказательство.

Пусть прямая СВ перпендикулярна плоскости α. АС — наклонная. Прямая а — прямая, проходящая через основание наклонной на плоскости α. (Рис.3)

Проведем прямую через основание наклонной AD и параллельную прямой СВ. Тогда прямая AD также перпендикулярна плоскости α и соответственно прямой а. Проведем плоскость β через прямые АD и CB. Тогда, если прямая а перпендикулярна проекции наклонной АВ, то она перпендикулярна плоскости β. А следовательно, любой прямой в этой плоскости, т.е. самой наклонной АС.

Следует отметить, что верно и обратное утверждение. Если прямая, проведенная на плоскости через основание наклонной ей перпендикулярна, то она перпендикулярна и проекции наклонной на эту плоскость.

Рис. 3 Теорема отрех перпендикулярах.

4. Признак перпендикулярности плоскостей

Теорема: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость перпендикулярна их прямой пересечения и пересекает их по перпендикулярным прямым.

Пусть даны две плоскости α и β, которые пересекаются по прямой с (Рис.4). Проведем плоскость γ, которая пересекает плоскости α и β по прямым а и b. Плоскость γ перпендикулярна прямой с. Прямые а и b также перпендикулярны прямой с. Следовательно плоскости α и β перпендикулярны.

Если взять другую плоскость, параллельную плоскости γ, например плоскость γ’, которая пересекает прямую с под прямым углом, она пересечет плоскости α и β по прямым a’ и b’, которые будут параллельны прямым а и b. По теореме о перпендикулярности прямых в пространстве прямые a’ и b’ также будут перпендикулярны, как и прямые а и b. Что и требовалось доказать.

Рис. 4 Признак перпендикулярности плоскостей.

Теорема: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Пусть α — плоскость. Прямая с перпендикулярна плоскости α. Точка А — точка пересечения прямой с и плоскости α (Рис.4.1). Проведем через прямую с плоскость β, которая будет пересекать плоскость α по прямой а. Необходимо доказать, что плоскости α и β перпендикулярны.

Проведем через точку А на плоскости α прямую b, перпендикулярную прямой а. Через прямые b и с проведем плоскость γ. Она перпендикулярна прямой а, так как прямая а перпендикулярна двум прямым b и с. Тогда плоскость β пересекает две плоскости α и γ по двум перпендикулярным прямым а и с. И пересекает прямую пересечения b под прямым углом. Следовательно плоскости α и β перпендикулярны.

Рис. 4.1 Перпендикулярность плоскостей.

Видео:Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

5. Расстояние между скрещивающимися прямыми

Теорема. Две скрещивающиеся прямые имеют только один общий перпендикуляр, который также является перпендикуляром между параллельными плоскостями, проведенными через эти прямые.

Доказательство. Пусть а и b две скрещивающиеся прямые (Рис.5). Проведем через них две плоскости α и β, параллельные друг другу. А от прямой а проведем перпендикуляры на плоскость β. Таким образом, получим плоскость γ, которая перпендикулярна обоим плоскостям α и β и пересекает плоскость β по прямой a’. Прямые а и a’ параллельны. Прямая a’ пересекает прямую b в точке А. Следовательно, один из перпендикуляров, проведенных от каждой точки прямой а на плоскость β, т.е. отрезок АВ и есть общий перпендикуляр между прямыми а и b.

Допустим, что существует еще один общий перпендикуляр между прямыми а и b это CD. Тогда два перпендикуляра пересекают прямые а и b в точках А,В,С,D, которые в свою очередь параллельны между собой. Следовательно через них можно провести плоскость. А в этой плоскости лежат и две прямые а и b, которые также будут параллельны между собой. А это противоречит условию, т.к. прямые а и b являются скрещивающимися. Следовательно у двух скрещивающихся прямых может быть только один общий перпендикуляр.

Отсюда следует, что расстояние между двумя скрещивающимися прямыми равно длине их общего перпендикуляра.