Презентация к уроку черчения по теме «Основные способы проецирования» 9 класс
- Просмотр содержимого документа «»Основные способы проецирования»»
- Лекция 2. Ортогональные проекции прямой
- 2.1. Задание прямой на эпюре
- 2.2. Прямые частного положения
- 2.3. Метод прямоугольного треугольника
- 2.4. Точка и прямая
- Упражнение
- Упражнение
- 2.5. Следы прямой
- 2.6. Взаимное расположение прямых
- 2.7. Проекции плоских углов
- Теорема о проецировании прямого угла в частном случае
- 2.8. Задачи для самостоятельного решения
- Отрезок прямой параллельной плоскости проекций изображается на ней точкой
- УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ ПРОЕКЦИЙ
- СЛЕДЫ ПРЯМОЙ ЛИНИИ
- ИЗОБРАЖЕНИЕ ВЗАИМНОГО ПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
- 🌟 Видео
Просмотр содержимого документа
«»Основные способы проецирования»»
Черчение 9 класс
Учитель: Большакова Ирина Павловна
МБОУ СОШ № 6 г.Димитровграда
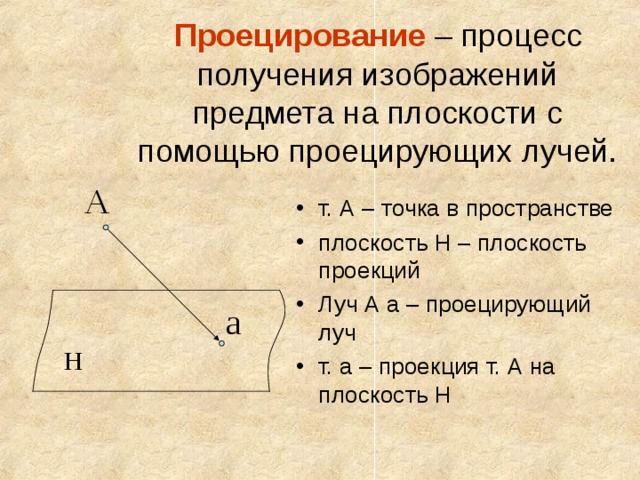
Проецирование – процесс получения изображений предмета на плоскости с помощью проецирующих лучей.
- т. А – точка в пространстве
- плоскость Н – плоскость проекций
- Луч А а – проецирующий луч
- т. а – проекция т. А на плоскость Н
Проекция – изображение предмета на плоскости, полученное с помощью проецирующих лучей.
- Проекция
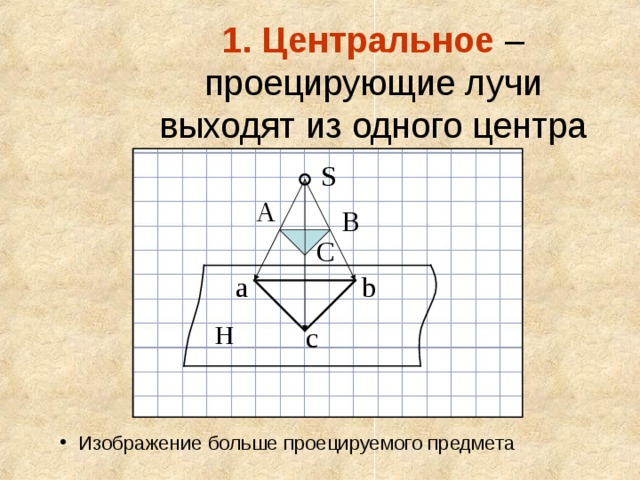
1. Центральное – проецирующие лучи выходят из одного центра
- Изображение больше проецируемого предмета
Применение центрального проецирования в жизни
2. Параллельное – проецирующие лучи проходят параллельно друг другу.
- косоугольное;
- прямоугольное.
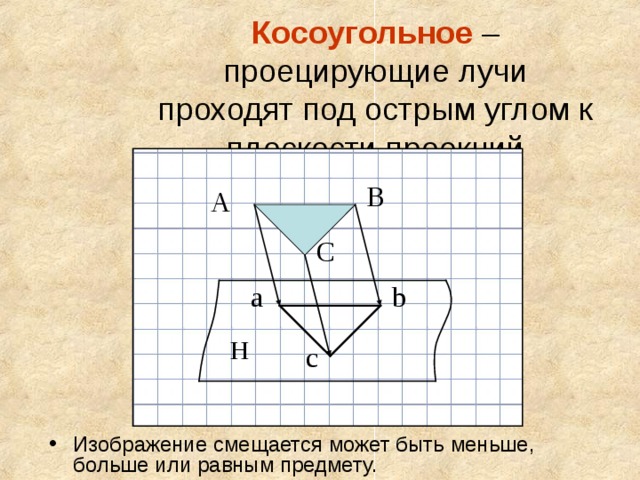
Косоугольное – проецирующие лучи проходят под острым углом к плоскости проекций
- Изображение смещается может быть меньше, больше или равным предмету.
Применение косоугольного проецирования в жизни
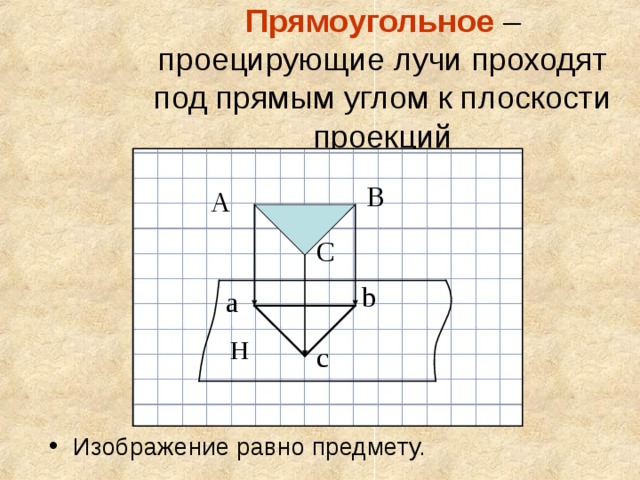
Прямоугольное – проецирующие лучи проходят под прямым углом к плоскости проекций
- Изображение равно предмету.
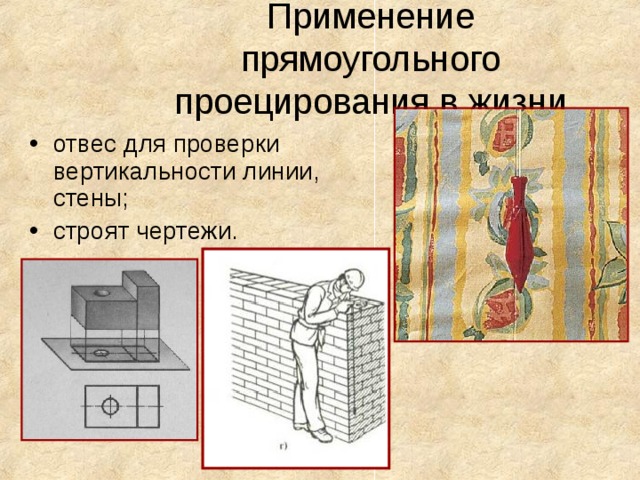
Применение прямоугольного проецирования в жизни
- отвес для проверки вертикальности линии, стены;
- строят чертежи.
Проверка понимания (да или нет).
- Прямоугольное проецирование – частный случай параллельного проецирования.
- При прямоугольном проецировании отрезки всегда изображаются в натуральную величину.
- При проецировании проекции точек обозначают заглавными буквами.
- Отрезок прямой параллельной плоскости проекций изображается на ней точкой.
- При прямоугольном проецировании сохраняется параллельность.
- Можно ли при проецировании прямоугольника получить треугольник.
- Отрезок прямой перпендикулярный плоскости проекций изображается на ней точкой
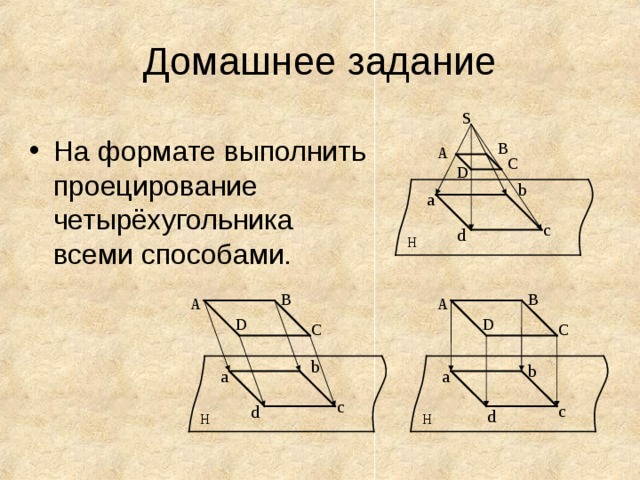
- На формате выполнить проецирование четырёхугольника всеми способами.
Видео:Проецирование точки на 3 плоскости проекцийСкачать

Лекция 2. Ортогональные проекции прямой
Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

2.1. Задание прямой на эпюре
Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.
а б
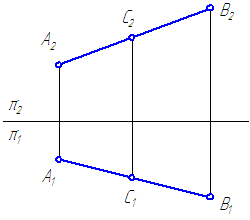
Рисунок 2.1 – Проекции прямой
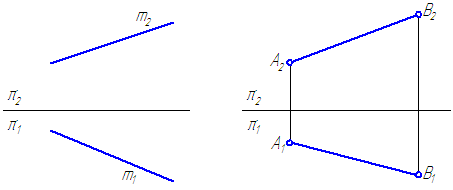
Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.
Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения .
Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.
Видео:Параллельность прямой к плоскостиСкачать

2.2. Прямые частного положения
Прямая, параллельная или перпендикулярная какой-либо плоскости проекций, называется прямой частного положения .
Прямые, параллельные плоскостям проекций, называются прямыми уровня .
Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).
Рисунок 2.2 – Эпюр горизонтали
Если отрезок параллелен плоскости проекций π1, то его фронтальная проекция А2В2 параллельна оси проекций π1/π2, а горизонтальная проекция отрезка А1В1 определяет истинную величину АВ:
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).
Рисунок 2.3 – Эпюр фронтали
Если отрезок параллелен плоскости проекций π2, то его горизонтальная проекция параллельна оси проекций π2/π1, а фронтальная проекция отрезка C2D2 определяет истинную величину CD.
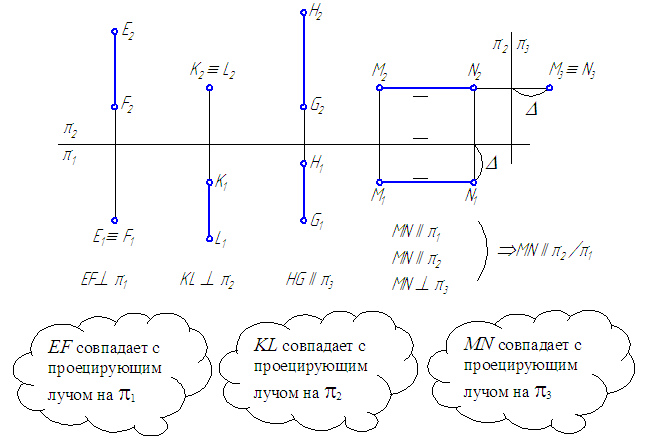
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).
Прямые, перпендикулярные плоскостям проекций, называются проецирующими .
Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).
Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).
Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).
Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH
Видео:Способ вращения. Определение истинной величины отрезка.Скачать

2.3. Метод прямоугольного треугольника
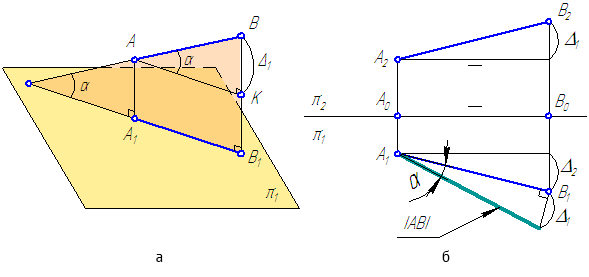
Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.
Рассмотрим положение отрезка АВ относительно горизонтальной плоскости проекций π1 (Рисунок 2.5).
Рисунок 2.5 – Определение истинной величины отрезка общего положения
На рисунке 2.5, а:
АА1 – расстояние от точки А до плоскости проекций π1;
ВВ1 – расстояние от точки В до плоскости проекций π1;
ΔАКВ – прямоугольный треугольник, в котором:
ВК=ВВ1–АА1=Δ1 – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π1 (то есть, разности координат Z точек А и В);
АВ – гипотенуза ΔАКВ – истинная величина.
При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.
Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π2
Видео:Определение длины отрезкаСкачать

2.4. Точка и прямая
Если точка принадлежит прямой, то её проекции:
- Принадлежат одноимённым проекциям данной прямой;
- Лежат на одной линии связи.
Рисунок 2.7 – Принадлежность точки прямой
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:
Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:
Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Упражнение
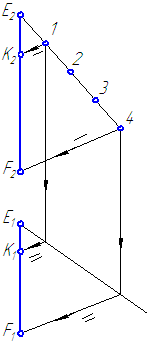
Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)
Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:
- Проведём произвольную прямую из любого конца любой проекции отрезка, например, Е2.
- Отложим на этой прямой от точки Е2 равные отрезки, количество которых равно сумме чисел, составляющих дробь (в нашем примере 1+3=4).
- Соединим последнюю точку 4 с другим концом фронтальной проекции отрезка – точкой F2.
- Из точки 1 проведём прямую, параллельную прямой (4—F2) до пересечения с проекцией E2F2, таким образом будет найдена фронтальная проекция искомой точки К2.
- Горизонтальную проекцию точки К1 получим путём построения линии проекционной связи до пересечения её с горизонтальной проекцией отрезка.
Видео:Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

Упражнение
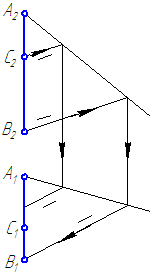
Определить принадлежность точки С отрезку прямой АВ (Рисунок 2.9).
Рисунок 2.9а – Решение упражнения 2. Способ 1.
Рисунок 2.9б – Решение упражнения 2. Способ 2.
Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.
Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать

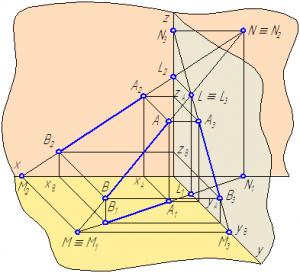
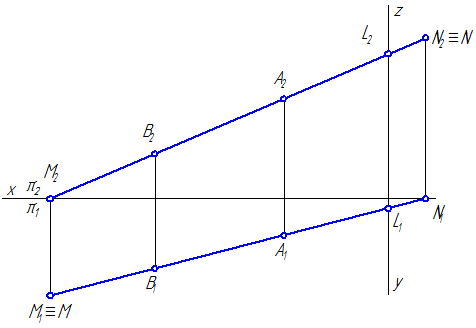
2.5. Следы прямой
След прямой – точка пересечения прямой с плоскостью проекций.
Прямая общего положения в общем случае может быть три следа:
- горизонтальный след M1– точка пересечения прямой с горизонтальной плоскостью проекций π1;
- фронтальный след N2– точка пересечения прямой с фронтальной плоскостью проекций π2;
- профильный след L3 – точка пересечения прямой с профильной плоскостью проекций π3.
След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:
- горизонтальный след совпадает со своей горизонтальной проекцией M≡M1,
- фронтальный – с фронтальной проекцией N≡N2,
- профильный – с профильной проекцией L≡L3 (Рисунок 2.10).
Рисунок 2.10 – Построение следов отрезка прямой АВ
Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).
Для построения горизонтального следа прямой АB необходимо:
- Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
- Из точки М2 провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.
Чтобы построить фронтальный след отрезка АB прямой, необходимо:
- Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
- Из точки N1 провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Ниже приводим алгоритм построения следов отрезка прямой АВ:
Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ
Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

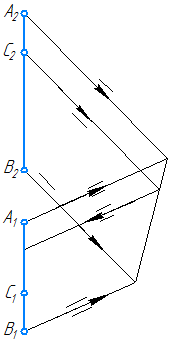
2.6. Взаимное расположение прямых
Две прямые в пространстве могут быть:
- параллельными;
- пересекающимися;
- скрещивающимися.
Параллельные прямые – прямые, пересекающиеся в несобственной точке.
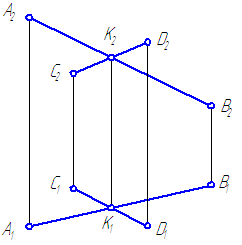
Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).
Рисунок 2.12 – Параллельные прямые
Пересекающиеся прямые – прямые, имеющие одну общую точку.
Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).
Рисунок 2.13 – Пересекающиеся прямые
Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).
Рисунок 2.14 — Скрещивающиеся прямые
Видео:УГЛЫ НАКЛОНА ЛИНИИ К ПЛОСКОСТЯМ ПРОЕКЦИЙ. ДЛИНА ОТРЕЗКА В ПРОСТРАНСТВЕ. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯСкачать

2.7. Проекции плоских углов
Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.
Рисунок 2.15
По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.
Видео:Проецирование прямой общего положенияСкачать

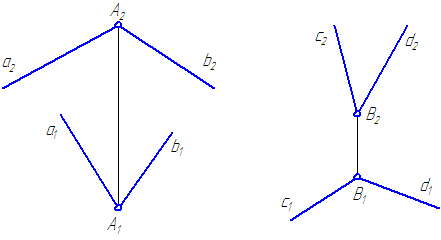
Теорема о проецировании прямого угла в частном случае
Теорема . Если одна из сторон прямого угла параллельна какой-либо плоскости, а другая – этой плоскости не перпендикулярна, то на эту плоскость прямой угол проецируется в виде прямого угла (Рисунок 2.16, а и б).
Обратная теорема . Если одна из двух пересекающихся прямых параллельна некоторой плоскости проекций и проекции этих прямых на эту же плоскость пересекаются под прямым углом, то в пространстве эти прямые взаимно перпендикулярны.
Рисунок 2.16 – Проецирование прямого угла
Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,
Видео:Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

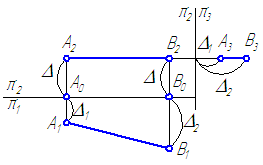
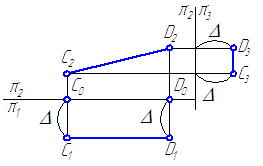
2.8. Задачи для самостоятельного решения
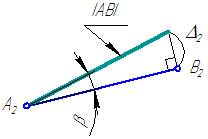
1. Построить отрезок прямой АВ // π1, равный 35 мм и наклонённый к π2 под углом 25° (Рисунок 2.17).
Рисунок 2.17
2. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π2 и π1.
3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π1 и 45° — к плоскости проекций π2.
4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π2/π1 (Рисунок 2.18).
Видео:Проецирование точки на три плоскости проекцийСкачать
Отрезок прямой параллельной плоскости проекций изображается на ней точкой
Прямая линия А В определяется двумя точками, которые находятся на концах отрезка. Прямоугольную проекцию отрезка А В можно построить следующим образом (рис. 89, а).
Опустив перпендикуляры из точек и на плоскость Н, получим проекции а и b этих точек. Соединив точки а и b прямой линией, получим искомую горизонтальную проекцию отрезка А В.
Если взять на отрезке прямой линии АВ точки А, С, D, Е, В (рис. 89, б) и из каждой точки опустить перпендикуляры на плоскость Н,то совокупность этих перпендикуляров можно рассматривать как плоскость Q, перпендикулярную к плоскости Н. Плоскость Q пересечет плоскость Н по прямой линии, на которой располагаются точки пересечения всех перпендикуляров с плоскостью Н. Так как эти точки являются проекциями точек отрезка А В,то, следовательно, и отрезок ab будет проекцией отрезка АВ. Таким образом, проекцию отрезка А В ни плоскости Я можно получить, если через отрезок А В провести плоскость , перпендикулярную к плоскости Н, до их взаимного пересечения. Линия пересечения плоскостей и будет горизонтальной проекцией отрезка АВ.
На рис. 89, в показано построение фронтальной проекции отрезка АВ. Плоскость Р перпендикулярна плоскости V.
Рассмотрим различные случаи расположения отрезков прямой линии по отношению к плоскостям проекций Н, V и W.
1. Прямая, перпендикулярная к плоскости V, называется фронтально-проецирующей прямой (рис. 90, а).
Из комплексного чертежа отрезка А В (рис. 90, б) видно, что горизонтальная проекция аb перпендикулярна к оси х и подлине равна отрезку AB фронтальная проекция а’b’ является точкой.
Если, например, резец расположить так, чтобы его длинные ребра были параллельны плоскостям V и Н, то ребро АВ будет фронтально-проецирующей прямой (рис. 90, в).
2. Прямая, перпендикулярная к плоскости H (рис. 91, а), называется горизонтально-проецирующей прямой.
Из комплексного чертежа отрезка (рис. 91, б) видно, что фронтальная проекция b’c’ перпендикулярна к оси х и по длине равна отрезку ВС, а горизонтальная проекция bс является точкой.
Ребро ВС резца на рис. 91, в является горизонтально-проецирующей прямой.
3. Прямая, перпендикулярная к плоскости H. называется профильно-проецирующей прямой (рис. 92, а).
На комплексном чертеже обе проекции отрезка — фронтальная и горизонтальная — параллельны оси Ох и по длине равны отрезку АВ (рис. 92, б). Профильная проекция а»b» отрезка АВ — точка.
Длинное ребро А В резца (рис. 92, в) — профильно-проецирующая прямая.
4. Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или сокращенно — горизонталью (рис. 93, а).
На комплексном чертеже горизонтали (рис. 93, б) видно, что фронтальная а’b’ и профильная a»b» проекции параллельны соответственно осям проекций Ох и Oy1 Горизонтальная проекция ab горизонтали А В расположена под углом к оси Ох и равна длине отрезка АВ.
Ребро А В (режущая кромка) головки резца (рис. 93, в) параллельно плоскости Н и представляет собой горизонталь.
5. Прямая, параллельная плоскости V, называется фронталью (рис. 94, а).
Горизонтальная проекция ab фронтали AB параллельна оси Ох (рис. 94, б).Фронтальная проекция а’b’ фронтали наклонена к оси Ох и равна действительной длине отрезка А В.Профильная проекция а»b» фронтали АВ параллельна оси Oz.
Ребро А В резца (рис. 94, в) параллельно плоскости V и, следовательно, представляет собой фронталь.
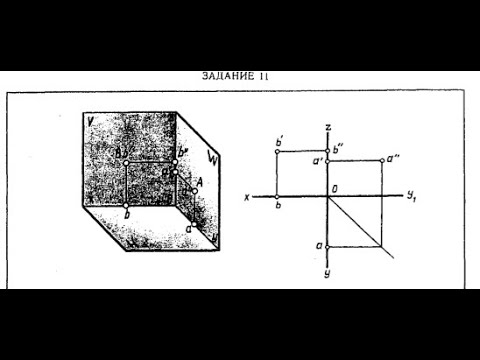
6. Прямая, не параллельная ни одной из трех плоскостей проекций, называется прямой общего положения.
Возьмем отрезок АВ прямой общего положения (рис. 95, а)и построим горизонтальную ab и фронтальную а’b’ проекции этого отрезка. Комплексный чертеж отрезка прямой общего положения показан на рис. 95, б.
По двум проекциям а’b’ и ab отрезка прямой общего положения можно, применяя известное уже правило , построить третью проекцию a»b» (рис. 95, б).
У отрезного резца (рис. 95, в) ребро представляет собой прямую общего положения.
Рассмотренные прямые часто применяются в построениях, поэтому, изучая их комплексные чертежи, надо запомнить, как та или иная проекция прямой располагается по отношению к осям проекций.
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ ПРОЕКЦИЙ
Горизонталь, фронталь и прямая общего положения расположены под углом к плоскостям проекций.
Угол прямой линии с плоскостью проекций определяется как острый угол между этой прямой и ее проекцией на данную плоскость. Например, отрезок фронтали АВ (рис. 96, а) составляет угол а с горизонтальной плоскостью проекций Н.
Разберем способ определения угла между прямой и плоскостью проекций на комплексном чертеже. Если прямая — фронталь, то, как видно из рис. 96, б, угол между фронталью и горизонтальной плоскостью проекций H на комплексном чертеже равен углу между фронтальной проекцией фронтали a’b’ и осью проекций x.
Ребро АВ резьбового резца (рис. 96, в) параллельно фронтальной плоскости проекций, т. е. ребро АВ — фронталь. Так как основание резца расположена на горизонтальной плоскости проекций H, то угол а является углом между прямой А и плоскостью Н. Таким образом, по чертежу резца можно определить угол а между ребром АВ и основанием резца. Следовательно, если прямая имеет какую-либо проекцию, равную действительной ее длине, то на комплексном чертеже угол между проекцией этой прямой и плоскостью проекций будет действительным углом.
СЛЕДЫ ПРЯМОЙ ЛИНИИ
Следом прямой линии называется точка пересечения прямой с плоскостью проекций.
Чтобы найти фронтальный след прямой АВ (рис. 97, а), необходимо продолжить ее горизонтальную проекцию ab до пересечения с осью x в точке v, а затем из точки v восстановить перпендикуляр к оси x и найти точку v’ пересечения этого перпендикуляра с продолжением фронтальной проекции отрезка.
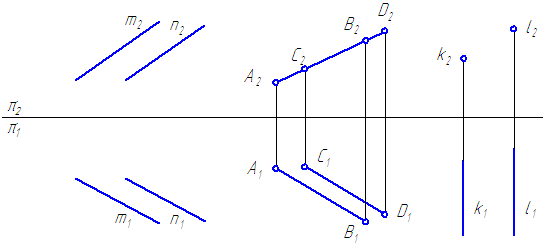
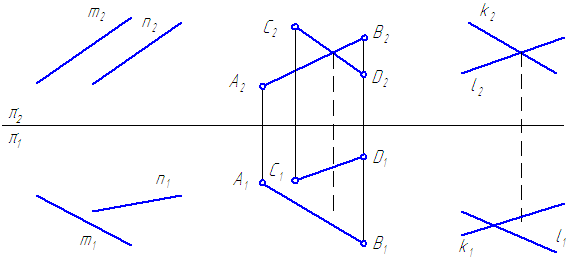
ИЗОБРАЖЕНИЕ ВЗАИМНОГО ПОЛОЖЕНИЯ ДВУХ ПРЯМЫХ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
Из курса начертательной геометрии известно, что:
а) если прямые параллельны в пространстве, то их одноименные проекции параллельны (рис. 98, );
б) если прямые пересекаются в точке , то их одноименные проекции тоже пересекаются (рис. 98, б); при этом проекции точки пересечения А обязательно располагаются на одном перпендикуляре к оси (на одной линии связи);
в) если точки пересечения проекций прямых, например, n’ и а не расположены на одном перпендикуляре к оси х (рис. 98, в), то прямые скрещиваются.
Точка v’ — искомый фронтальный след прямой АВ или точнее — фронтальная проекция фронтального следа; точка v — горизонтальная проекция горизонтального следа; точка h’ — фронтальная проекция горизонтального следа.
На комплексном чертеже отрезка эти построения выполняются аналогично (рис. 91, б).
Из чертежа видно, что одна из двух проекций каждого следа прямой расположена на оси х.
🌟 Видео
Лекция 1. Классификация прямых линий.Скачать

Проецирование точек на разных октантахСкачать

2. Построение недостающей фронтальной проекции отрезка прямойСкачать

Проецирование точкиСкачать

Построение недостающей проекции отрезка прямой линии, лежащей в заданной плоскостиСкачать

Задача №1 Определение натуральной величины отрезка прямой (АВ) методом прямоугольного треугольникаСкачать

Задание 14 Боголюбов С.К. Проецирование ОТРЕЗКА на три плоскости проекцийСкачать