Отрезок прямой параллельной основаниям трапеции заключенный

Приветствуем Вас на сайте! Здесь Вы можете ознакомиться с подробными решениями задач по физике, математике, экономике, химии. В открытом доступе имеются примеры заданий гуманитарных дисциплин — английский, история, МХК и др. Грамотные преподаватели в режиме обсуждения на сайте готовы бесплатно консультировать Вас по интересным (с нашей точки зрения) задачам.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

вторник, 8 июня 2010 г.

Задача на построение по геометрии

Параллельно основаниям трапеции проведите прямую, отрезок которой заключенный внутри трапеции делился бы ее диагоналями на три равные части.

Решение

Это прямая, проходящая через точки Н и Е. Докажем это.

1) Проведём прямые ВО || CD и СО₁ || AB. Докажем, что точки О и О₁ совпадают в точке О. Приведём векторное доказательство (ниже векторы):
ВО + О₁С = ВС
ВО = ВА + АО
О₁С = О₁D + DC
BA + AO + О₁D + DC = BC
AO + О₁D = BC − DC − BA = BC + AB + CD = AD
Чтобы равенство выполнялось, точки О и О₁ должны совпадать. Доказано.

2) Н и Е — точки пересечения диагоналей соответственно в параллелограммах АВСО и BCDO. Поэтому ВН = НО, а СЕ = ЕО. Из этого следует, что НЕ — средняя линия треугольника ВСО, и поэтому НЕ || BC.

3) Докажем равенство некоторых треугольников:
∠АВО = ∠ВОА как накрест лежащие
∠ВНР = ∠ОНЕ как вертикальные
ВН = НО
Значит, △ВНР = △НЕО по стороне и двум прилежащим к ней углам. А отсюда следует, что РН = НЕ

∠OCD = ∠COB как накрест лежащие
∠HEO = ∠CET как вертикальные
CE = EО
Значит, △CET = △НЕО по стороне и двум прилежащим к ней углам. А отсюда следует, что ET = НЕ

Получили, что РН = ЕН = ЕТ, что и требовалось доказать

Видео:Задача повышенной сложности из ОГЭ. Найти длину прямой, параллельной основаниям трапецииСкачать

Отрезок прямой , параллельной основания трапеции , заключенный внутри трапеции , разбивается диагоналями на 3 отрезка?

Геометрия | 5 — 9 классы

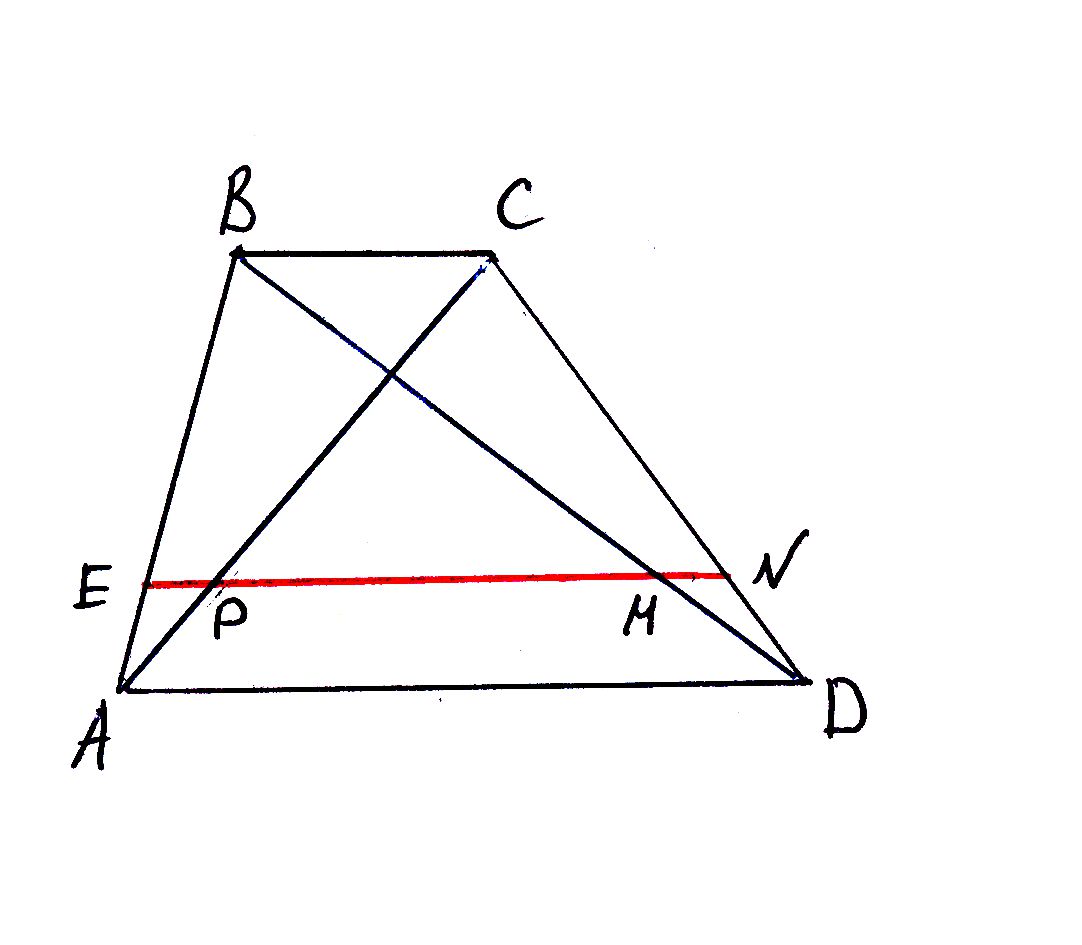
Отрезок прямой , параллельной основания трапеции , заключенный внутри трапеции , разбивается диагоналями на 3 отрезка.

Докажите, что крайние из них равны между собой.

Если прямая проходит ниже точки пересечения диагоналей, то крайние из них являются отрезками, пропорциональными малому основанию.

При этом коэффициент пропорциональности определяется расстоянием прямой от большого основания.

Если эта прямая (параллельная основаниям) EN делит высоту трапеции, или диагональ, или боковую строну, или любой другой отрезок прямой, концы которого лежат на разных основаниях трапеции, в следующем отношении —

(К примеру) AE / AB = q

то крайние отрезки будут иметь длину

где b = BC — малое основание.

Все это следует из простого подобия пар треугольников (ABC и AEP) и (DMN и DBC), а так же теоремой о пропорциональности отрезков секущих между параллельными прямыми (из чего следует, что MD / BD = ND / CD = AP / AC = q).

Для прямых, проходящих выше точки пересечения диагоналей, рассматриваются треугольники, у которых основанием является большое основание трапеции.

С тем же результатом : ))).

Видео:Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые #математика #огэ #впрСкачать

ПОЖАЛЙСТА?

1. каждая из сторон треугольника разделена на три равных отрезка и точки деления соединены отрезками.

Найдите пениметр образовавшейся при этом фигуры, если периметр исходного треугольника равен р 2.

Основания трапеции равны 14см и 20 см.

Одна из боковых сторон разделена на три равные части и через точки деления проведены прямые параллельные основаниям трапеции.

Найдите отрезки этих прямых, заключенные внутри трапеции.

Видео:Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

Основы трапеции равны 3см и 6см ?

Основы трапеции равны 3см и 6см .

Прямая параллельная основаниям трапеции проходит через точку пересечения диагоналей трапеции .

Найдите длину отрезка этой прямой , ограниченного боковыми сторонами трапеции .

Задача 8 класса.

Видео:Как найти отрезок, проходящий через точку пересечения диагоналей трапеции параллельно её основаниям?Скачать

4. Параллельно основаниям трапеции проведите прямую, отрезок которой, заключенный внутри трапеции, делился бы ее диагоналями на три равные части?

4. Параллельно основаниям трапеции проведите прямую, отрезок которой, заключенный внутри трапеции, делился бы ее диагоналями на три равные части.

Видео:№386. Докажите, что отрезок, соединяющий середины боковых сторон трапеции,Скачать

Основания трапеции равны 15см и 24см?

Основания трапеции равны 15см и 24см.

Одна из боковых сторон разделена на три равные части, и через точки деления проведены прямые, параллельные основаниям трапеции.

Найдите отрезки этих прямых , заключенных внутри трапеции.

Видео:Отрезок, соединяющий середины диагоналей трапецииСкачать

Прямая, параллельная основаниям трапеции, проходит через точку пересечения её диагоналей?

Прямая, параллельная основаниям трапеции, проходит через точку пересечения её диагоналей.

Найдите длину отрезка этой прямой, заключённого между боковыми сторонами трапеции, если основания трапеции равны 9 и 18.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Докажите, что длина заключённого внутри трапеции отрезка прямой, проходящей через точку пересечения диагоналей трапеции параллельно её основаниям, равна 2ab : a + b (дробь), где a и b — длины основани?

Докажите, что длина заключённого внутри трапеции отрезка прямой, проходящей через точку пересечения диагоналей трапеции параллельно её основаниям, равна 2ab : a + b (дробь), где a и b — длины оснований трапеции.

Видео:№569. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллеленСкачать

Найдите длину отрезка прямой, параллельной основаниям трапеции и делящей трапецию на две равновеликие фигуры заключенного между сторонами трапеции?

Найдите длину отрезка прямой, параллельной основаниям трапеции и делящей трапецию на две равновеликие фигуры заключенного между сторонами трапеции.

Длины основания трапеции равны 6 и 8.

Видео:Трапеция | Задачи 11-24 | Решение задач | Волчкевич |Уроки геометрии в задачах 7-8Скачать

Основания трапеции 5 см и 14 см ?

Основания трапеции 5 см и 14 см .

Боковая сторона трапеции разделена на три равные части , и через точки деления проведены прямые, параллельные основанию до пересечения с другой боковой стороной.

Найдите длины отрезков этих прямых, заключённые внутри трапеции.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Основания трапеции 5 см и 14 см ?

Основания трапеции 5 см и 14 см .

Боковая сторона трапеции разделена на три равные части , и через точки деления проведены прямые, параллельные основанию до пересечения с другой боковой стороной.

Найдите длины отрезков этих прямых, заключённые внутри трапеции.

Видео:8 класс, 6 урок, ТрапецияСкачать

Основания трапеции равны 10 и 6 см?

Основания трапеции равны 10 и 6 см.

Боковую сторону трапеции разделили на 4 равных отрезка и через точки деления провели прямые, параллельные основаниями.

Найдите отрезки этих прямых, принадлежащие трапеции.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос Отрезок прямой , параллельной основания трапеции , заключенный внутри трапеции , разбивается диагоналями на 3 отрезка?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Угол АCD равен 65 гр.

Сумма углов параллелограмма и вообще любого четырёхугольника равна 360⁰. В параллелограмме противоположные углы равны, как и стороны — это его основное свойство. Запишем сумму углов параллелограмма : 360⁰ = 2α + 2β, гдеα, β — это его углы. У нас с..

1) 180 — 125 = 55( внутренний угол С) 2) В равнобедренном треугольнике углы при оснаваний равны отсюда следует, что угол А = 55 градусов. 3) 180 — 55 — 55 = 70 градусов( угол В).

1) 12 : 4 = 3 см Площадь : 3×3 = 9 см2 Ответ : каждая сторона должна быть 3 см, площадь 9 см2.

Треугольники АВ1С1 и АВС подобные. Коэффицент подобия = АС1 : С1С = 0. 75. ВС = В1С1 : 0. 75 = 6 : 0. 75 = 8.

Диаметр окружности вписанной в трапецию равен ее высоте, так что высота равна 48 * 2 = 96.

Дуга АС = 2угла АВС = 2 * 80 = 160 градусов360 — 160 = 200 градусов — дуги АВ и ВСАВ = 2х, ВС = 3х2х + 3х = 2005х = 200х = 40Значит угол АСВ = 2 * 40 / 2 = 40 градусов угол ВАС = 3 * 40 / 2 = 60 градусовОтвет : 80, 60 , 40.

Неразвернутый угол — это угол, который меньше 90 градусов. Надо взять транспортир, например : отметить 30 градусов и начертить.

2) d = 13 a = 12 b = корень из d ^ 2 — a ^ 2 = 5 p = 2(a + b) = 2(12 + 5) = 34.

Видео:Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Интересные свойства трапеции

В работе представлены свойства трапеции, не рассматриваемые в школьном базовом курсе геометрии

Видео:Построить трапецию по основаниям и двум сторонамСкачать

Скачать:

Предварительный просмотр:

Видео:35. Геометрия на ЕГЭ по математике. Трапеция.Скачать

Подписи к слайдам:

Проектная работа « Интересные свойства трапеции » Выполнили : ученицы 10 класса Кудзаева Эллина Баззаева Диана МКОУ СОШ с. Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года

Цель работы: Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства .

Свойства трапеции: Если трапеция разделена прямой, параллельной ее основаниям, равным a и в , на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен a В к

Свойство отрезка, проходящего через точку пересечения диагоналей трапеции . Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с

Свойства трапеции: Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК Р М О К

Свойства равнобедренной трапеции: Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону. О С В А Д . Е О

Свойства равнобедренной трапеции: Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне О А В С Д

Свойства равнобедренной трапеции: В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии. С В А Д h

1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства: 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен

Свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r ). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC

Доказательство : Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m , FD=n . Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а

I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º . 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность .

I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции. Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K — середина BS. Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD. Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.

III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно. Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.

I V. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.

Если равнобедеренную трапецию со сторонами а,в,с , d можно вписать и около неё можно описать окружности, то площадь трапеции равна

💡 Видео

ОГЭ 23 | КАК НАЙТИ ОТРЕЗКИ ЗАКЛЮЧЕННЫЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИСкачать

Середины диагоналей трапеции. (Полуразность оснований)Скачать

Найдите длину отрезка внутри трапецииСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Геометрия 8. Урок 8 - Теорема Фалеса - теорияСкачать