Отрезки соединяющие середины противоположных сторон выпуклого четырехугольника авсд (2 видео)

Отрезки, соединяющие середины противоположных сторон выпуклого четырёхугольника, равны между собой. Найдите площадь четырёхугольника,

Содержание

Ваш ответ
решение вопроса
Похожие вопросы
VIII.3. Задачи к теоретической карте № 8
В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении 9:13
🔍 Видео

Видео:№101. Докажите, что отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаютсяСкачать

Ваш ответ

Видео:ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

решение вопроса

Видео:№808* Точки А и С — середины противоположных сторон произвольного четырехугольника, а точки B и DСкачать

VIII.3. Задачи к теоретической карте № 8

№1. Если отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника, перпендикулярны, то диагонали четырехугольника равны. Доказать.

План доказательства.

1. Параллелограмм MNPK – ромб.

Используемые факты из теоретической карты: 1.1.

№2. Диагонали трапеции взаимно перпендикулярны, длина одной из них равна 6 см. Длина отрезка, соединяющего середины оснований равна 4,5 см. Найти площадь трапеции.

Дополнительные построения:

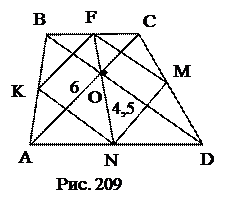
KFMN – параллелограмм, вершины

которого – середины сторон трапеции.

1. KFMN – прямоугольник.

Ответ: см. Используемые факты из теоретической карты: 1.1; 1.2.

№3. Доказать, что отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке.

Проиллюстрируем фрагменты условия задачи на двух чертежах.

О – точка пересечения отрезков, соединяющих середины противоположных сторон четырехугольника ABCD (рис. 210.1). L – середина диагонали АС, F- середина диагонали BD (рис. 210.2).

1. О – середина NK. 2. NLKF – параллелограмм. 3. О – середина NK и LF.

Используемые факты из теоретической карты: 1.1.

№4. Найти площадь параллелограмма, если длины его сторон равны a и b, а угол между диагоналями, противолежащий стороне длины а, равен .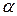

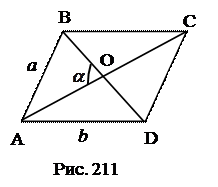
План решения.

1. Выразить а 2 через АО и ОВ.

2. Выразить b 2 через АО и OD.

3. Выразить из (1) и (2) АО∙ОВ и АС∙BD.

Ответ: .

Используемые факты из теоретической карты: 2.

№5. Сумма диагоналей ромба равна m, а его площадь S. Найти сторону ромба.

План решения.

1. Выразить m 2 через АС и BD.

2. Выразить АС∙ BD через S.

3. Выразить АС 2 + BD 2 через m и S.

4. Выразить АО 2 +ОВ 2 через m и S.

Ответ:

Используемые факты из теоретической карты: 2.

№6.В ромб с острым углом 60°вписан четырёхугольник так, что его вершинами являются основания высот, проведённых из точки пересечения диагоналей ромба к его сторонам, Найти отношение площади четырёхугольника к площади ромба.

План решения.

Пусть сторона ромба равна а.

1. Выразить NQ через а.

2. Выразить S_MNPQ через NQ, а затем через а.

3. Выразить S_ABCD через а.

4. Hайти искомое отношение.

Используемые факты из теоретической карты: 2.

№7.Доказать,что площадь треугольника равна произведения двух медиан на синус угла между ними.

План доказательства.

1. Выразить площадь треугольника ВС₁А₁

через площадь данного треугольника S.

2. Выразить площадь четырехугольника

3. Выразить площадь данного треугольника

через площадь четырехугольника АС₁А₁С

и площадь треугольника ВС₁А₁.

Используемые факты из теоретической карты: 2.

№8. Диагональ трапеции вписанной в круг радиуса R, образует с ее боковыми сторонами углы 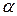и . Найти площадь трапеции.

План решения.

6. АС (по теореме синусов ∆ACD).

Ответ: .

Используемые факты из теоретической карты: 2.

№9. Четырехугольник разделен диагоналями на четыре треугольника. Наименьшие площади трех из них равны 10, 20 и 30. Найти площадь данного четырехугольника.

План решения.

1. Установить соответствие между треугольниками и площадями.

2. Найти площадь четвертого треугольника.

Используемые факты из теоретической карты: 3.

№10. В трапеции ABCD(AВ||CD). О – точка пересечения диагоналей АС и BD. Площади треугольников АВО и CDO равны соответственно 10 и 40. Найти
площадь трапеции.

План решения.

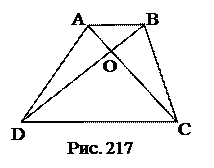
Используемые факты из теоретической карты: 3.

№11. Площадь трапеции равна 3, основания относятся как 1:2. Найдите площади треугольников, на которые трапеция разделена диагоналями.

План решения.

4. 2S₁+ S₁+2S₁=3. 5. S₁, S₂, S₃, S₄.

Ответ:

Используемые факты из теоретической карты: 3.

№12. В равнобокую трапецию вписана окружность радиуса 2. Найти площадь трапеции, если длина боковой стороны равна 10.

План решения.

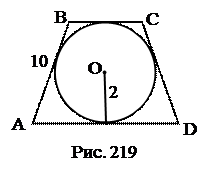
Используемые факты из теоретической карты: 4,5.

№13. Около окружности, радиус которой равен 1,2 см описан четырехугольник ABCD, у которого АВ=3 см, ВС=2 см, AD=4 см. Найти площадь этого четырехугольника.

План решения.

Используемые факты из теоретической карты: 5, 4.

№14. Около круга описана равнобедренная трапеция, площадь которой равна 32 см 2 . Найти стороны трапеции, если угол при большем основании равен 30 0 .

План решения.

1. Выразить ВС+AD, ВF, S_ABCD через АВ.

2. АВ. 3. AD+BC. 4. AF. 5. BC, AD.

Ответ: 8 см, см, см, 8 см.

Используемые факты из теоретической карты: 5.

№15. Равнобедренная трапеция ABCD (AD||BC, AD>BC) описана около окружности с центром О. О₁ – точка пересечения диагоналей трапеции. Площади треугольников АО₁В и АОВ равны 3 и 4. Найти углы трапеции.

Проиллюстрируем фрагменты условия задачи на двух чертежах.

1. АВ∙r. 2. Выразить полупериметр ABCD через АВ. 3. S_ABCD.

4. Составить систему уравнений (Рис. 222.2).

5. S₂, S₄. 6. AD: ВС. 7. Выразить AD через ВС. 8. Выразить АК через ВС.

9. Выразить АВ через ВС. 10. АК:АВ=cos

Ответ: 60 0 , 120 0 .

Используемые факты из теоретической карты: 3, 4, 5.

№ 16. В четырехугольнике проведены все биссектрисы внутренних углов. Доказать, что пересечением биссектрис образовался четырехугольник, около которого можно описать окружность.

План доказательства.

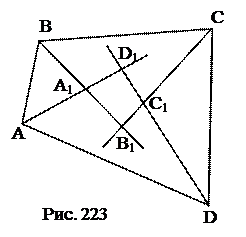
1. ÐВВ₁С выразить через ÐВ иÐС четырехугольникаABCD.

2. ÐАD₁D выразить через ÐA иÐD четырехугольникаABCD.

Используемые факты из теоретической карты: 6.

№17. Из точки М, лежащей вне окружности, проведены два луча, пересекающие окружность в точках А, В, С и D. Доказать, что треугольники АМС и DMB подобны.

1. .

2. .

3. .

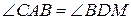
Используемые факты из теоретической карты: 6.

№18. Через середину С дуги АВ проведены прямые CD и CE, пересекающие хорду АВ в точках H и F. Доказать, что около четырехугольника DHFE можно описать окружность.

План решения.

2. .

3. .

Используемые факты из теоретической карты: 6.

№19. Через вершину С треугольника АВС проведены его внутренняя биссектриса CD и внешняя биссектриса. Из вершины В проведен перпендикуляр к стороне АВ, пересекающий внешнюю биссектрису в точке К. Доказать, что около четырехугольника CDBK можно описать окружность (точка D лежит на стороне АВ)

План доказательства.

CD – биссектриса внутреннего угла АСВ,

СК – биссектриса внешнего угла DCB.

2. ÐDCK+ÐDBK=180 0 .

Используемые факты из теоретической карты: 6.

IX. ТРАПЕЦИЯ И ПАРАЛЛЕЛОГРАММ

Видео:Как решать С4, геометрия. Урок 12. #ЕГЭ по математике 2014. Середины противоположных сторонСкачать

В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении 9:13

В выпуклом четырёхугольнике середины противоположных сторон соединены отрезками, причём один из них делит этот четырёхугольник на две равновеликие фигуры, а другой делит площадь в отношении $9:13$. а) Доказать, что данный четырёхугольник является трапецией. б) Найти отношение меньшего основания этой трапеции к большему.

а) Рассмотрим выпуклый четырёхугольник $QMNP$ (см. рис.). Пусть $E$ — середина $MQ$, $F$ — середина $NP$, причём $S_=S_$.

Проведём отрезки $EN$ и $EP$. Заметим, что
$S_= / EF⋅ FNsin ∠ EFN= / EF⋅ FP sin ∠ EFP=S_$, так как $NF=FP$ и $sin ∠ EFN=sin (180°-∠ EFN)=sin ∠ EFP$. Отсюда $S_=S_$ ($S_=S_-S_$, $S_=S_-S_$). Опустим в $▵ MNE$ высоту $NN_1$, в $▵ EPQ$ — высоту $PP_1$. Получим: $ / ME⋅ NN_1= / EQ⋅ PP_1$. Но $ME=EQ$, следовательно, $NN_1=PP_1$. Но тогда в четырёхугольнике $N_1NPP_1$ $∠ NN_1P_1=∠ N_1P_1P=90°$, $NN_1=PP_1$, то есть $N_1NPP_1$ — прямоугольник. Значит, $N_1P_1∥ NP$, $MQ∥ NP$. Из предположения о том, что $MN∥ QP$, следует, что отрезок, соединяющий середины сторон $MN$ и $QP$, делит параллелограмм $MNPQ$ на две равновеликие фигуры. Но по условию это не так. Значит, $MN ∦ QP$. Следовательно, $MNPQ$ — трапеция. б) По условию второй отрезок $AB$ делит четырёхугольник так, что площадь $ANPB$ относится к площади $ABQM$ как $9:13$ (см. рис.).

$S_:S_=9:13$. $AB$ — средняя линия трапеции, $AB= / $. $S_= / ⋅ h_1$; $S_= / ⋅ h_2$, где $h_1$ — высота трапеции $ANPB$; $h_2$ — высота трапеции $ABQM$. Так как $NP∥ MQ$, а $AB$ — средняя линия и $AB∥ NP$ и $AB∥ MQ$, то расстояния от $AB$ до $NP$ и от $AB$ до $MQ$ равны, то есть $h_1=h_2$. Отсюда, $<S_> / <S_>= </ > / </ >= <NP+/ > / </ +MQ>= / $, $ / = / $, $39NP+13MQ=27MQ+9NP$, $30NP=14MQ$, $ / = / = / $.

🔍 Видео

Планиметрия_03_05Скачать

Планиметрия_03_02Скачать

ЕГЭ Математика 16 Задание Планиметрическая задача Четырехугольники Середины сторонСкачать

Задание №26 ОГЭ по математикеСкачать

Биссектрисы пересекаются в одной точке| Задачи 28-33 | Решение задач | Волчкевич|Уроки геометрии 7-8Скачать

Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать

8 класс, 3 урок, ЧетырехугольникСкачать

ОГЭ без рекламы математика вариант 13 и 14 задача 25Скачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

№386. Докажите, что отрезок, соединяющий середины боковых сторон трапеции,Скачать

УСТНАЯ ЗАДАЧА - МАТ В 3 ХОДА!Скачать

№430. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположныеСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

23. Выпуклые четырехугольникиСкачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Отрезки соединяющие середины противоположных сторон выпуклого четырехугольника авсд

Ваш ответ

решение вопроса

Похожие вопросы

VIII.3. Задачи к теоретической карте № 8

🔍 Видео