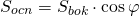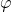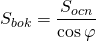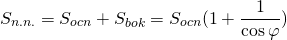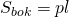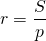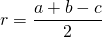Высота пирамиды проецируется в центр вписанной окружности если (6 видео)

Пирамида

Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.

По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Содержание

Некоторые свойства пирамиды
Виды пирамид
Узнать ещё
Пирамиды, в которых двугранные углы при основании равны
Высота пирамиды проецируется в центр вписанной окружности
Пирамида
Некоторые свойства пирамиды
Виды пирамид
Высота пирамиды проецируется в центр вписанной окружности
Пирамида
💡 Видео

Видео:Пирамиды, в которых высота проходит через центр вписанной в основание окружностиСкачать

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр

Верно и обратное.

Видео:Условия проецирования вершины пирамиды в центр описанной окружностиСкачать

Виды пирамид

Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Видео:Условия проецирования вершины пирамиды в центр вписанной окружности в треугольник, ромб, трапецию.Скачать

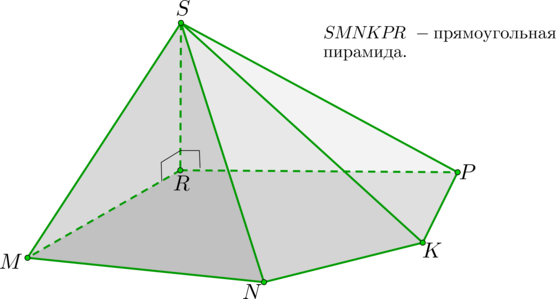
Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Видео:ЕГЭ Задание 14 Теорема Менелая в стереометрической задачеСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:ПЛОЩАДЬ КОЛЬЦА. Сделай выбор: на чьей ты стороне?Скачать

Пирамиды, в которых двугранные углы при основании равны

Теперь рассмотрим пирамиды, в которых двугранные углы при основании равны: каковы их свойства, как изображаются.

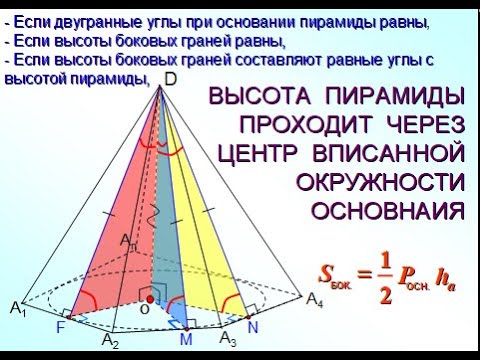
Если все двугранные углы при ребрах основания равны, то

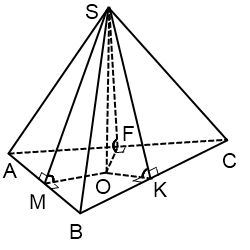
1) вершина пирамиды проецируется в центр вписанной в основание окружности ;

2) основание пирамиды является ортогональной проекцией ее боковой поверхности , поэтому площадь основания пирамиды можно найти по формуле

— двугранный угол при основании пирамиды. Чаще эту формулу используют для нахождения площади боковой поверхности пирамиды:

Соответственно, площадь полной поверхности пирамиды равна

3) площадь боковой поверхности в этом случае также может быть найдена по формуле

где p — полупериметр основания, l — высота боковой грани, проведенная из вершины пирамиды.

Прямоугольные треугольники, образованные высотой пирамиды, высотами боковых граней, проведенными из вершины пирамиды, и их проекциями (равными радиусу вписанной окружности), равны. Поэтому также

— высоты боковых граней, проведенные из вершины пирамиды, равны;

— высоты боковых граней образуют с высотой пирамиды равные углы.

Решение задач на пирамиды, в которых двугранные углы при основании равны (или — пирамиды, в которых высоты боковых граней равны либо образуют с высотой пирамиды равные углы), начинается с чертежа.

Если основание пирамиды — треугольник

Центр вписанной в треугольник окружности лежит строго внутри треугольника и является точкой пересечения его биссектрис.

Радиус вписанной окружности ищем по формуле

где S — площадь треугольника, p — его полу периметр.

Если в основании такой пирамиды лежит прямоугольный треугольник, чертеж немного иной.

Это связано со свойствами параллельного проектирования: параллельность прямых сохраняется. Радиусы, перпендикулярные катетам, и отрезки, прилежащие к прямому углу треугольника, образуют квадрат, который на чертеже изображается параллелограммом.

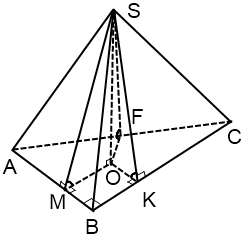
Радиус вписанной в прямоугольный треугольник окружности ищем по формуле

где a и b — катеты, c — гипотенуза.

Если основание пирамиды — параллелограмм

Из всех параллелограммов вписать окружность можно только в ромб (и квадрат как его частный случай). Поэтому, если в задаче известно, что все двугранные углы при основании равны (или высоты боковых граней пирамиды равны либо образуют с высотой пирамиды равные углы), а в основании лежит параллелограмм, то речь может идти только о ромбе (или квадрате).

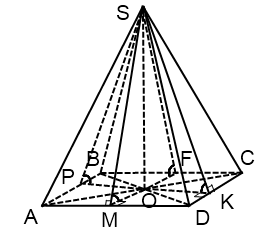
O — точка пересечения диагоналей ромба (квадрата).

Радиус вписанной в ромб окружности можно искать по формуле

Кроме того, радиус вписанной в ромб окружности равен половине его высоты.

Если основание пирамиды — произвольный четырехугольник

О — точка пересечения биссектрис четырехугольника ABCD.

Радиус вписанной в четырехугольник окружности ищем все по той же формуле

Поскольку вписать в четырехугольник окружность можно тогда и только тогда, когда суммы длин его противоположных сторон равны,

Если основание пирамиды — трапеция

O — точка пересечения биссектрис трапеции.

Радиус вписанной в трапецию окружности

а также радиус вписанной окружности равен половине высоты трапеции.

Если все двугранные углы при основании пирамиды равны (либо высоты боковых граней пирамиды равны, либо высоты боковых граней составляют с пирамидой равные углы), а в основании пирамиды — правильный многоугольник, то это — правильная пирамида.

Видео:Куда проецируется вершина пирамиды, если все боковые грани наклонены под одним углом к основанию?Скачать

Высота пирамиды проецируется в центр вписанной окружности

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Пирамида

По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Верно и обратное.

Видео:№246. Высота треугольной пирамиды равна 40 см, а высота каждой боковой грани, проведеннаяСкачать

Виды пирамид

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

Видео:Треугольник и окружность #shortsСкачать

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Видео:Наибольшее и наименьшее зн. функции Ч. 3Скачать

Высота пирамиды проецируется в центр вписанной окружности

14.1. Определение пирамиды и её элементов

Определение. Пирамидой называется многогранник, у которого одна грань — многоугольник, а остальные грани — треугольники с общей вершиной (рис. 95, 96).

Многоугольник называется основанием пирамиды, остальные грани — боковыми гранями пирамиды, их общая вершина — вершиной пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами её основания, называются боковыми рёбрами пирамиды .

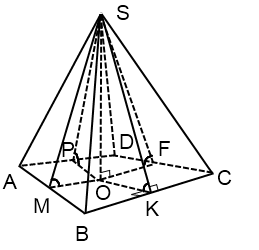
Пирамиду с основанием АВСDЕ и вершиной Р обозначают PABCDE .

Перпендикуляр, опущенный из вершины пирамиды на плоскость её основания, называется высотой пирамиды . Длину этого перпендикуляра также называют высотой пирамиды.

Пирамида называется n-угольной, если её основанием является n-угольник .

На рисунке 96 изображена четырёхугольная пирамида PABCD, у которой: четырёхугольник ABCD — основание пирамиды; точка Р — вершина пирамиды; отрезки РA, РВ, PC, PD — боковые рёбра пирамиды; отрезки АВ, ВС, CD, DA — стороны (рёбра) основания пирамиды; отрезок РО — высота пирамиды; треугольники РАВ, РВС, PCD, PDA — боковые грани пирамиды.

У n- угольной пирамиды имеется ( n + 1) вершин, 2 n рёбер и ( n + 1) граней. Диагоналей пирамида не имеет. В пирамиде различают плоские углы при её вершине и двугранные углы при её рёбрах. Двугранным углом при ребре пирамиды называют содержащий пирамиду двугранный угол, образованный плоскостями граней, проходящими через данное ребро.

Треугольную пирамиду (рис. 97) называют также тетраэдром ( « тетраэдр» по-гречески означает «четырёхгранник» ) . Тетраэдр — это многогранник с наименьшим числом граней. Любая грань тетраэдра может быть принята за его основание; это отличает тетраэдр от всех остальных пирамид.

Любую пирамиду можно разбить на некоторое число тетраэдров, а любой выпуклый многогранник — на некоторое число пирамид. Для этого достаточно, например, взять любую точку внутри данного многогранника и соединить её отрезками со всеми его вершинами. Такое разбиение часто используется при нахождении объёмов многогранников.

14.2. Некоторые виды пирамид

Если все боковые рёбра пирамиды составляют с плоскостью основания равные углы, то : а ) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды ; б ) все боковые рёбра пирамиды равны между собой.

Доказательств о. а) Пусть отрезок РО — высота пирамиды PABCDEF, все рёбра которой составляют с плоскостью основания угол ϕ (рис. 98). Тогда прямоугольные треугольники РОА, POB, POC, POD, РОЕ и POF, имея общий катет РО, равны между собой (по катету и острому углу ϕ ) . Из равенства этих треугольников следует: ОА = OВ = ОС = OD = OE = OF, т. е. вершины основания пирамиды равноудалены от основания О её высоты РО. Это означает, что точка О — центр окружности, описанной около основания ABCDEF данной пирамиды.

б) Из ОА = OВ = ОС = OD = ОЕ = OF следует, что боковые рёбра РА, РВ, PC, PD, РЕ, PF пирамиды равны, как наклонные, имеющие равные проекции, т. е. РА = РВ = PC = PD = РЕ = PF. Что и требовалось доказать. ▼

Вы самостоятельно можете доказать обратные утверждения.

1. Если основание высоты пирамиды совпадает с центром окружности, описанной около её основания, то: а) все боковые рёбра пирамиды образуют с плоскостью основания равные углы; б) все боковые рёбра пирамиды равны между собой.

2. Если все боковые рёбра пирамиды равны, то: а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды; б) все боковые рёбра пирамиды составляют с плоскостью её основания равные между собой углы.

Также имеет место следующее утверждение.

Если высота пирамиды пересекает её основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в её основание.

Доказательств о. Пусть РО — высота пирамиды PABCDE, боковые грани которой образуют с плоскостью основания пирамиды двугранные углы, равные ϕ (рис. 99).

Проведём высоты РН 1 , РH 2 , РН 3 , PH 4 , РH 5 боковых граней.

Тогда по теореме о трёх перпендикулярах получаем OH 1 ⟂ AB, OH 2 ⟂ BC, OH 3 ⟂ CD, OH 4 ⟂ DE, OH 5 ⟂ EA, следовательно, ∠ OH 1 P = ∠ OH 2 P = ∠ OH 3 P = ∠ OH 4 P = ∠ OH 5 P = ϕ . Поэтому △ OH 1 P = △ OH 2 P = △ OH 3 P = △ OH 4 P = △ OH 5 P (как прямоугольные с общим катетом OP и острым углом ϕ ) . Из равенства этих треугольников следует ОН 1 = OH 2 = OH 3 = ОН 4 = ОН 5 , т. е. точка О — основание высоты РО пирамиды — равноудалена от всех сторон многоугольника ABCDE. Это означает, что точка O является центром окружности, вписанной в основание ABCDE данной пирамиды. Теорема доказана. ▼

Самостоятельно докажите обратное утверждение.

Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.

Перечислим ещё несколько часто встречающихся в задачах видов пирамид.

• Пирамида, ровно одна боковая грань которой перпендикулярна плоскости основания. Высота такой пирамиды лежит в этой, перпендикулярной основанию, грани (рис. 100).

• Пирамида, две соседние боковые грани которой перпендикулярны плоскости основания. Высотой такой пирамиды служит боковое ребро, общее для этих граней (рис. 101).

• Пирамида, две не соседние боковые грани которой перпендикулярны плоскости основания. Высота такой пирамиды лежит на прямой пересечения плоскостей этих граней (рис. 102).

14.3. Правильная пирамида

Определение. Пирамида называется правильной, если её основание — правильный многоугольник и вершина пирамиды проектируется в центр этого основания.

Из определения следует алгоритм построения изображения правильных пирамид, что, в свою очередь, доказывает существование таких пирамид.

Для построения изображения правильной пирамиды достаточно построить изображение соответствующего правильного многоугольника (основания пирамиды) и его центра. Затем из построенного центра провести перпендикуляр к плоскости многоугольника и выбрать на этом перпендикуляре (в качестве вершины пирамиды) любую точку, отличную от центра многоугольника. Соединив отрезками прямых эту точку со всеми вершинами многоугольника, получим изображение правильной пирамиды.

На рисунке 103, а, б, в построены изображения правильных пирамид: а) треугольной; б) четырёхугольной; в) шестиугольной.

Правильные пирамиды обладают замечательным свойством.

В правильной пирамиде все боковые рёбра равны, а все боковые грани — равные равнобедренные треугольники.

Доказательств о. Рассмотрим правильную n- угольную пирамиду РА 1 А 2 . A n . Пусть точка O — центр n- угольника A 1 A 2 A 3 . A n ; отрезок РО — перпендикуляр к плоскости основания пирамиды (рис. 104).

Так как центр правильного многоугольника является центром окружности, описанной около этого многоугольника, то ОА 1 = OA 2 = OA 3 = . = OA n (как радиусы описанной окружности). Тогда равны боковые рёбра пирамиды, как наклонные к плоскости её основания, имеющие равные проекции, т. е. PA 1 = PA 2 = PA 3 = . = PA n .

Таким образом, имеем:

РА 1 = РA 2 = . = PA n (как боковые рёбра);

A 1 A 2 = A 2 A 3 = . = A n A 1 (как стороны правильного n- угольника).

Следовательно, треугольники PA 1 A 2 , РA 2 A 3 , . PA n A 1 являются равнобедренными и по третьему признаку равенства треугольников равны между собой.

Это свойство правильной пирамиды можно доказать при помощи поворота пирамиды вокруг оси, содержащей её высоту.

Так как точка О — центр правильного n- угольника A 1 A 2 A 3 . A n , лежащего в основании правильной пирамиды PA 1 A 2 . A n , РО — перпендикуляр к плоскости её основания, то при вращении данной пирамиды вокруг оси ОР на угол, равный (где k = 1, 2, 3, . n ), происходит самосовмещение этой пирамиды: вершины основания пирамиды отображаются на его же вершины (основание совмещается с самим собой); вершина Р (как точка оси вращения) отображается на себя. Следовательно, боковые рёбра пирамиды отображаются на боковые рёбра, а боковые грани пирамиды — на её боковые грани. А так как вращение вокруг прямой — движение, то все боковые рёбра правильной пирамиды равны между собой, а грани являются равными равнобедренными (почему?) треугольниками. Утверждение доказано. ▼

Следствием доказанного выше является утверждение.

Все боковые рёбра правильной пирамиды образуют с плоскостью основания равные углы, а все боковые грани — равные двугранные углы.

Докажите это предложение самостоятельно.

Высота боковой грани правильной пирамиды, проведённая к ребру её основания, называется апофемой пирамиды. На рисунке 104 отрезок РН — одна из апофем пирамиды.

Все апофемы правильной пирамиды равны вследствие равенства всех её боковых граней.

Имеют место признаки правильной пирамиды:

Пирамида, в основании которой лежит правильный многоугольник, является правильной, если: а) все её боковые рёбра равны; б) все её боковые рёбра образуют с плоскостью основания равные углы; в) все её боковые грани — равные равнобедренные треугольники.

Докажите это самостоятельно.

 ЗАДАЧА (2.245). Высота правильной четырёхугольной пирамиды равна h и образует с боковой гранью угол α . Через сторону основания пирамиды проведена плоскость, перпендикулярная противоположной грани и пересекающая её. Найти площадь сечения.

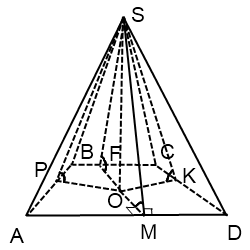
Дан о: PABCD — правильная пирамида (рис. 105); РО — высота пирамиды, РО = h ; ∠ OPF = α .

Решени е. Первый спосо б . Пусть отрезок EF — средняя линия основания пирамиды. Тогда AD ⟂ EF, AD ⟂ PF ⇒ АD ⟂ ( РEF ) ⇒ ( PEF ) ⟂ ( ADP ) (по признаку перпендикулярности двух плоскостей). Поэтому прямая PF является ортогональной проекцией прямой РO на плоскость ADP. Значит, ∠ OPF — угол между высотой PO и боковой гранью ADP пирамиды: ∠ OPF = α .

Далее имеем: AD ⟂ ( PEF ), ВС || AD ⇒ ВC ⟂ ( PEF ) ⇒ прямая ВС перпендикулярна любой прямой плоскости PEF. Поэтому если FL ⟂ РЕ (в плоскости PEF ) , то BС ⟂ FL. Тогда FL ⟂ ВС, FL ⟂ PE ⇒ FL ⟂ ( BCP ) ⇒ ( ADL ) ⟂ ( ВCР ) (по признаку перпендикулярности двух плоскостей); при этом ( ADL ) ∩ ( ВСР ) = МK , МK || AD, так как плоскости ВСР и АDL проходят через параллельные прямые ВС и AD. Значит, сечение ADKM — трапеция, у которой FL — высота (почему?), откуда

S сеч = • FL.

Найдём AD, МK и FL.

В △ OPF ( ∠ POF = 90 ° ):

OF = OP • tg α = h • tg α ; PF = = = PE.

EF = 2 FO = 2 h • tg α = ВС.

В плоскости PEF получаем:

FL ⟂ РЕ, РО ⟂ EF ⇒ ∠ EFL = ∠ OPE = α .

Тогда в △ ЕFL : FL = ЕF • cos α = 2 h • tg α • cos α = 2 h sin α ;

в △ PLF ( ∠ PLF = 90 ° , ∠ PFL = 90 ° – 2 α ):

PL = PF • sin (90 ° – 2 α ) = PF • cos 2 α = .

Так как MK | | BC, то △ МKР ∾ △ ВСР, откуда

= ⇒ MK = = =
= 2 h tg α • cos 2 α .

AD = EF = 2 h • tg α , FL = 2 h • sin α , MK = 2 h • tg α • cos 2 α .

S сеч = • FL = • 2 h • sin α =
= = 4 h 2 • sin 2 α • cos α .

Замечание. Отрезок MK можно найти следующим образом. Сечением данной пирамиды плоскостью, проходящей через прямую MK параллельно основанию пирамиды, является квадрат MKD 1 A 1 (см. рис. 105). F 1 = A 1 D 1 ∩ PF. У этого квадрата LF 1 = MK. Найдём F 1 L .

В треугольнике LFF 1 имеем ∠ FLF 1 = α ( LF 1 || EF ) ,

∠ F 1 FL = ∠ OFP – ∠ OFL = (90 ° – α ) – α = 90 ° – 2 α ;

∠ FF 1 L = 180 ° – ∠ OFF 1 = 90 ° + α . Тогда по теореме синусов

= ⇒
⇒ LF 1 = = .

Значит, MK = LF 1 = 2 h • tg α • cos 2 α .

Второй спосо б . Пусть точки M 1 , K 1 , L 1 — ортогональные проекции на плоскость основания соответственно точек М, K, L (рис. 105, 106). Так как плоскости АСР, BDP и EFP перпендикулярны плоскости основания пирамиды, то ортогональными проекциями прямых PC, РВ и РЕ на эту плоскость являются соответственно прямые АС, BD и EF. Следовательно, M 1 ∈ BD, K 1 ∈ AC, L 1 ∈ EF, причём четырёхугольник ADK 1 M 1 — равнобедренная трапеция.

Таким образом, трапеция ADK 1 M 1 — ортогональная проекция сечения ADKM. Это означает, что S ADKM = . Найдём . Так как диагонали квадрата взаимно перпендикулярны и M 1 K 1 || AD, то OL 1 = L 1 K 1 , OF = FD. Значит,

= • L 1 F = • FL 1 = .

S ADKM = = = 4 h 2 • sin 2 α • cos α .

Ответ: 4 h 2 • sin 2 α • cos α .

1 4.4. Площади боковой и полной поверхностей пирамиды

Поверхность пирамиды состоит из основания и боковых граней. В этой связи различают боковую и полную поверхности пирамиды, а также их площади.

Площадью боковой поверхности пирамиды (обозначают S бок ) называется сумма площадей всех её боковых граней: S бок = S 1 + S 2 + . + S n , где S 1 , S 2 , . S n — площади боковых граней пирамиды.

Площадью полной поверхности пирамиды (обозначают S полн ) называется сумма площадей всех её граней, т. е. сумма площади основания пирамиды и площади её боковой поверхности.

Из определения следует: S полн = S бок + S осн .

О площади боковой поверхности правильной пирамиды имеет место следующая теорема.

Теорема 18. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды.

Доказательств о. PA 1 A 2 . A n — правильная пирамида, a — длина её апофемы (рис. 107).

Боковые грани правильной пирамиды — равные равнобедренные треугольники, у которых основаниями являются стороны правильного n- угольника A 1 A 2 . A n , а высоты равны апофеме пирамиды, т. е.

РE 1 = РE 2 = PE 3 = . = PE n = a.

S бок = S △ PA 1 A 2 + S △ PA 2 A 3 + . + S △ PA n A 1 =
= A 1 A 2 • PE 1 + A 2 A 3 • PE 2 + . + A n A 1 • PE n =
= a • ( A 1 A 2 + A 2 A 3 + . + A n A 1 ) = P • a,

где Р — периметр основания пирамиды. Теорема доказана. ▼

Теорема 19. Если все боковые грани пирамиды наклонены к плоскости основания под углом ϕ и высота пересекает основание, то S бок = .

Доказательств о. Пусть отрезок PO — высота пирамиды РA 1 A 2 A 3 . A n , все боковые грани которой образуют с плоскостью основания углы, равные ϕ (рис. 108); отрезки PH 1 , PH 2 , . PH n — высоты боковых граней. Тогда (по теореме о трёх перпендикулярах) OH 1 ⟂ A 1 A 2 , OH 2 ⟂ A 2 A 3 , . OH n ⟂ A n A 1 . Значит,

∠ OH 1 P = ∠ OH 2 P = ∠ OH 3 P = .
. = ∠ OH n P = ϕ .

Так как точка О является центром круга, вписанного в основание пирамиды (почему?), то эта точка лежит внутри n- угольника A 1 A 2 A 3 . A n . Поэтому n- угольник A 1 A 2 . A n является объединением непересекающихся треугольников A 1 OA 2 , A 2 OA 3 , . A n OA 1 . Эти треугольники являются ортогональными проекциями на плоскость основания пирамиды её соответствующих боковых граней. По теореме о площади ортогональной проекции многоугольника имеем:

S △ A 1 OA 2 = S △ A 1 PA 2 • cos ϕ ,
S △ A 2 OA 3 = S △ A 2 PA 3 • cos ϕ ,
.
S △ A n OA 1 = S △ A n PA 1 • cos ϕ .

Сложив почленно эти равенства, получим S осн = S бок • cos ϕ , откуда S бок = . Теорема доказана. ▼

Так как все боковые грани правильной пирамиды образуют с плоскостью основания равные двугранные углы (пусть величина этих углов равна ϕ , см. рис. 107), то для площади боковой поверхности и площади основания правильной пирамиды также справедлива формула

S бок = .

14 . 5 . Свойства параллельных сечений пирамиды

Если плоскость α параллельна основанию пирамиды и пересекает её, то в сечении пирамиды получается некоторый многоугольник (рис. 109).

Теорема 20. Если пирамида пересечена плоскостью, параллельной основанию, то: 1) боковые рёбра и высота делятся этой плоскостью на пропорциональные части; 2) в сечении получается многоугольник, подобный основанию; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Доказательств о. 1) Пусть сечением пирамиды PABCD плоскостью α , параллельной плоскости β её основания, является четырёхугольник A 1 B 1 C 1 D 1 (см. рис. 109).

Проведём высоту РО данной пирамиды и обозначим O 1 = РО ∩ α .

Рассмотрим гомотетию с центром Р , при которой плоскость основания данной пирамиды отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание ABCD пирамиды на её параллельное сечение — многоугольник А 1 В 1 С 1 D 1 , при этом вершины А, В, С, D основания пирамиды — на вершины соответственно A 1 , B 1 , C 1 , D 1 , а точку O — на точку O 1 (почему?).

Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

= = = = = k, (*)

где k — коэффициент гомотетии . Это означает, что параллельное сечение пирамиды делит её рёбра и высоту на пропорциональные части. А поскольку гомотетия является подобием, то многоугольник A 1 B 1 C 1 D 1 , являющийся параллельным сечением пирамиды, подобен её основанию ABCD .

Вследствие того, что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии, а k = РO 1 : РО , где РO 1 и РО — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

S A 1 B 1 C 1 D 1 : S ABCD = k 2 = : PO 2 .

Следствие. Плоскость, параллельная основанию пирамиды и пересекающая её, отсекает пирамиду, подобную данной.

14.6. Усечённая пирамида

Плоскость α , параллельная основанию пирамиды PABCD и пересекающая её, делит эту пирамиду на два многогранника: пирамиду РA 1 B 1 C 1 D 1 и многогранник ABCDA 1 B 1 C 1 D 1 (см. рис. 109).

Многогранник ABCDA 1 B 1 C 1 D 1 (рис. 110) называют усечённой пирамидой. Грани ABCD и A 1 B 1 C 1 D 1 , лежащие в параллельных плоскостях, называются соответственно нижним и верхним основаниями усечённой пирамиды , остальные грани — её боковыми гранями . Так как нижнее и верхнее основания усечённой пирамиды гомотетичны (т. 20), то все её боковые грани — трапеции.

Таким образом, усечённой пирамидой называется часть полной пирамиды, заключённая между её основанием и параллельным ему сечением.

У n- угольной усечённой пирамиды 2 n вершин, 3 n рёбер, ( n + 2) грани и n ( n – 3) диагоналей.

Высотой усечённой пирамиды называется перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого. Длину этого перпендикуляра также называют высотой усечённой пирамиды. На рисунке 110 отрезки О 1 О, B 1 K — высоты усечённой пирамиды.

Усечённая пирамида называется правильной, если она получена из правильной пирамиды (рис. 111).

Из теоремы 20 следует, что основания правильной усечённой пирамиды — подобные правильные многоугольники, а боковые грани — равные равнобедренные трапеции.

Высоты этих трапеций, соединяющие середины их оснований, называются апофемами усечённой пирамиды . Все её апофемы равны между собой.

Отрезок OO 1 , соединяющий центры оснований правильной усечённой пирамиды, является её высотой .

Площадью боковой поверхности усечённой пирамиды называется сумма площадей всех её боковых граней.

Для правильной усечённой пирамиды имеет место

Теорема 21. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему .

Для доказательства теоремы достаточно площадь одной из боковых граней пирамиды умножить на их число. В результате получим формулу S бок = • h , где Р 1 , P 2 — периметры нижнего и верхнего оснований усечённой пирамиды, h — её апофема.

Проведите доказательство теоремы самостоятельно.

Полная поверхность усечённой пирамиды — это объединение её оснований и боковой поверхности, поэтому для усечённой пирамиды

S полн = S бок + S 1 + S 2 ,

где S 1 и S 2 — площади большего и меньшего оснований этой пирамиды.

Для усечённой пирамиды, у которой все двугранные углы при рёбрах большего основания равны ϕ , справедливо: S бок = . (Для вывода этой формулы достаточно учесть следующий факт: если R и r — радиусы окружностей, вписанных соответственно в большее и меньшее основания данной пирамиды, то S 1 = 0,5 • P 1 • R , S 2 = 0,5 • P 2 • r, cos ϕ = , где h — высота боковой грани этой пирамиды.)

14 . 7 . Объём пирамиды

Лемма. Две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики .

Доказательств о. Пусть пирамиды РАВС и P 1 A 1 B 1 C 1 имеют высоты, равные H , и равновеликие основания с площадью S ; их объёмы — соответственно V 1 и V 2 . Докажем, что V 1 = V 2 .

Расположим пирамиды РАВС и P 1 A 1 B 1 C 1 так, чтобы их основания лежали в одной плоскости, а сами пирамиды были расположены по одну сторону от этой плоскости (рис. 112). Тогда любая плоскость, параллельная плоскости оснований и пересекающая первую пирамиду, пересекает и вторую, причём по теореме о параллельных сечениях пирамиды площади этих сечений равны. Следовательно, на основании принципа Кавальери равны и объёмы этих пирамид. Лемма доказана. ▼

Теорема 22. Объём любой треугольной пирамиды равен одной трети произведения площади основания на высоту.

Доказательств о. Пусть А 1 AВC — данная треугольная пирамида с вершиной A 1 и основанием ABC (рис. 113). Дополним эту пирамиду до треугольной призмы ABCA 1 B 1 C 1 с тем же основанием, одним из боковых рёбер которой является боковое ребро АA 1 данной пирамиды. Это означает, что высота призмы равна высоте данной пирамиды.

Призма АВCA 1 B 1 C 1 является объединением трёх треугольных пирамид с общей вершиной A 1 : A 1 ABC, A 1 BB 1 C 1 и A 1 BCC 1 . Основания BB 1 C 1 и BCC 1 пирамид A 1 BB 1 C 1 и A 1 BCC 1 равны, а высота у них общая. Значит, по лемме эти пирамиды имеют равные объёмы.

Будем считать точку В вершиной пирамиды A 1 BB 1 C 1 , a △ A 1 B 1 C 1 — её основанием. Тогда эта пирамида равновелика пирамиде А 1 AВС, так как у них общая высота, а основания АВС и A 1 B 1 C 1 равновелики (как основания призмы). Таким образом, призма ABCA 1 B 1 C 1 является объединением трёх равновеликих пирамид, одной из которых является данная пирамида A 1 ABC. Это означает, что объём V пирамиды A 1 АВС составляет одну треть объёма призмы ABCA 1 B 1 C 1 , т. е. V = S ocн • Н, где Н — длина высоты призмы. Но построенная призма и данная пирамида имеют общую высоту, длина которой равна Н, следовательно, объём треугольной пирамиды вычисляется по формуле

V = S осн • H ,

где Н — длина высоты данной пирамиды. Теорема доказана. ▼

На рисунке 114 изображены треугольная призма ABCDEF и составляющие её три равновеликие треугольные пирамиды ABDF, ABCF и BDEF .

Для вычисления объёма n- угольной пирамиды PA 1 A 2 . A n (рис. 115) разобьём её основание A 1 A 2 . A n диагоналями A 1 A 3 , A 1 A 4 , . A 1 A n – 1 на треугольники с общей вершиной A 1 . Тогда данная пирамида разбивается в объединение пирамид PA 1 A 2 A 3 , PA 1 A 3 A 4 , . PA 1 A n – 1 A n с общей вершиной Р и общей высотой, которая равна высоте данной пирамиды. Основаниями этих пирамид являются треугольники разбиения основания данной пирамиды. Это означает (свойство 2 объёмов), что объём V пирамиды PA 1 A 2 . A n равен сумме объёмов V 1 , V 2 , . V n – 2 треугольных пирамид соответственно PA 1 A 2 A 3 , PA 1 A 3 A 4 , . PA 1 A n – 1 A n .

Пусть длина высоты пирамиды равна Н, площадь её основания — S, а площади треугольников разбиения этого основания равны S 1 , S 2 , . S n – 2 . Это означает, что S 1 + S 2 + . + S n – 2 = S. Тогда получаем:

V = V 1 + V 2 + . + V n – 2 = H ( S 1 + S 2 + . + S n – 2 ) = S • H.

Таким образом, объём любой пирамиды вычисляется по формуле

V = S осн • H ,

где S осн — площадь основания, Н — длина высоты пирамиды.

Итак, доказана теорема.

Теорема 23. Объём любой пирамиды равен одной трети произведения площади основания на высоту. ▼

14.8. Об объёме тетраэдра

У тетраэдра за основание можно принять любую его грань, на каждую из которых можно провести высоту тетраэдра из вершины, противоположной этой грани. Поэтому для объёма V одного и того же тетраэдра имеют место соотношения

V = S 1 • h 1 = S 2 • h 2 = S 3 • h 3 = S 4 • h 4 ,

где S k и h k ( k = 1, 2, 3, 4) — площадь грани и длина опущенной на неё высоты. Эти соотношения часто используют при решении задач.

Заметим, что не в любом тетраэдре все четыре высоты пересекаются в одной точке (для сравнения — все три высоты любого треугольника пересекаются в одной точке). Тетраэдр, все высоты которого пересекаются в одной точке, называется ортоцентрическим.

Интересен также тетраэдр (рис. 116, а ), все грани которого равны. Такой тетраэдр называется равногранным. Его развёрткой является остроугольный треугольник (рис. 116, б ).

Докажите самостоятельно, что в равногранном тетраэдре:

— скрещивающиеся рёбра попарно равны;

— все высоты равны;

— сумма плоских углов трёхгранного угла при каждой вершине тетраэдра равна 180 ° ;

— двугранные углы при скрещивающихся рёбрах тетраэдра равны.

Не менее интересен следующий факт. Пусть дан тетраэдр A 1 C 1 BD . Проведём через каждое его ребро плоскость, параллельную скрещивающемуся с ним ребру. Проведённые шесть плоскостей при пересечении образуют некоторый параллелепипед АВСDA 1 В 1 C 1 D 1 (рис. 117), параллельные грани ABCD и A 1 B 1 C 1 D 1 которого содержат скрещивающиеся рёбра А 1 C 1 и BD данного тетраэдра. Тогда расстояние между основаниями АВСD и А 1 В 1 С 1 D 1 полученного параллелепипеда равно длине его высоты и равно расстоянию между скрещивающимися рёбрами А 1 C 1 и BD данного тетраэдра.

Этот параллелепипед можно разбить на пять тетраэдров — данный тетраэдр A 1 С 1 ВD и ещё четыре тетраэдра: A 1 ABD ; ВВ 1 A 1 C 1 ; C 1 CBD ; DD 1 A 1 C 1 . Объём каждого из четырёх последних тетраэдров равен одной трети высоты h параллелепипеда, умноженной на половину площади его основания ABCD , т. е. шестой части объёма V полученного параллелепипеда.

V A 1 C 1 BD = V – 4 • V = V = h • S ABCD = h • AC • BD • sin ϕ =
= h • A 1 C 1 • BD • sin ϕ ,

где ϕ — угол между диагоналями АС и BD параллелограмма ABCD . А так как AC || A 1 C 1 , то величина угла между скрещивающимися диагоналями A 1 С 1 и BD тетраэдра А 1 С 1 BD также равна ϕ .

Мы получили: объём тетраэдра равен одной шестой произведения длин любых двух его скрещивающихся рёбер, расстояния между ними и синуса угла между скрещивающимися прямыми, содержащими эти рёбра.

Отметим ещё несколько очевидных и менее очевидных свойств тетраэдров, связанных с их объёмами.

1. Объёмы тетраэдров с равными основаниями относятся как их высоты, опущенные на эти основания.

2. Объёмы тетраэдров с равными высотами относятся как площади их оснований.

3. Объёмы тетраэдров, имеющих равные трёхгранные углы, относятся, как произведения длин рёбер, образующих эти углы.

Используя рисунок 118, вы сможете легко доказать третье утверждение.

14.9. Объём усечённой пирамиды

Теорема 24. Объём усечённой пирамиды, у которой площади оснований равны S 1 и S 2 , а высота — Н , вычисляется по формуле

V = H ( S 1 + + S 2 ) .

Доказательств о. Пусть дана усечённая пирамида (рис. 119), у которой S 1 > S 2 , а высота OO 1 = H. Дополним эту пирамиду до полной пирамиды с вершиной Р. Объём V данной усечённой пирамиды равен разности объёмов полной и дополнительной пирамид.

Если длина высоты PO 1 дополнительной пирамиды равна x , то высота PO полной пирамиды равна H + x .

Выразим х через S 1 , S 2 и Н. По теореме 20 (o площадях параллельных сечений пирамиды) имеем

S 1 : S 2 = ( H + x ) 2 : x 2 ⇒ : = ( H + x ) : x ⇒
⇒ x = .

Поэтому для объёма V усечённой пирамиды находим

V = S 1 ( H + x ) – S 2 • x = ( S 1 • H + ( S 1 – S 2 ) • x ) =
= = ( S 1 H + ( + ) H ) =
= H ( S 1 + + S 2 ) ,

Видео:ТОП-5 ошибок в геометрии | МатематикаСкачать

Пирамида

Определение

Пирамида – это многогранник, составленный из многоугольника (A_1A_2. A_n) и (n) треугольников с общей вершиной (P) (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: (PA_1A_2. A_n) .
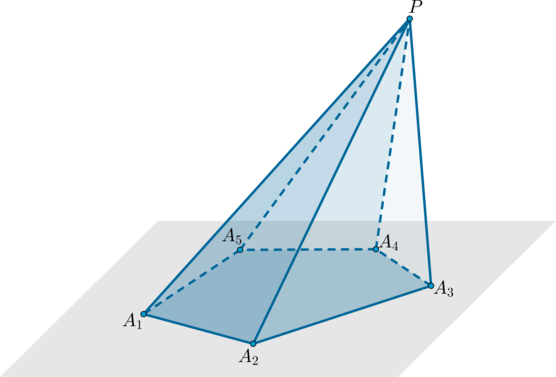
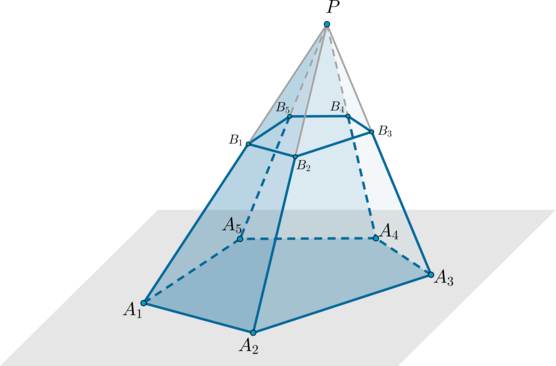
Пример: пятиугольная пирамида (PA_1A_2A_3A_4A_5) .

Треугольники (PA_1A_2, PA_2A_3) и т.д. называются боковыми гранями пирамиды, отрезки (PA_1, PA_2) и т.д. – боковыми ребрами, многоугольник (A_1A_2A_3A_4A_5) – основанием, точка (P) – вершиной.

Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

Пирамида, в основании которой лежит треугольник, называется тетраэдром.

Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:

((a)) боковые ребра пирамиды равны;

((b)) высота пирамиды проходит через центр описанной около основания окружности;

((c)) боковые ребра наклонены к плоскости основания под одинаковым углом.

((d)) боковые грани наклонены к плоскости основания под одинаковым углом.

Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.

Теорема

Условия ((a), (b), (c), (d)) эквивалентны.

Доказательство

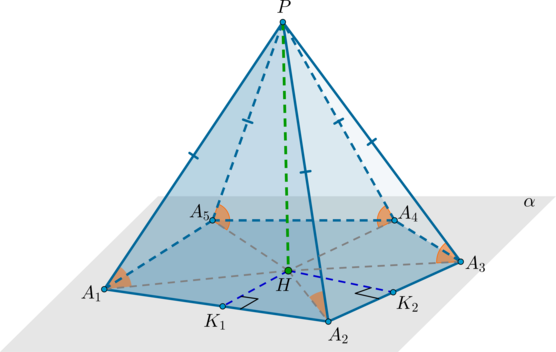
Проведем высоту пирамиды (PH) . Пусть (alpha) – плоскость основания пирамиды.

1) Докажем, что из ((a)) следует ((b)) . Пусть (PA_1=PA_2=PA_3=. =PA_n) .

Т.к. (PHperp alpha) , то (PH) перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники (PA_1H, PA_2H, PA_3H. PA_nH) – прямоугольные. Значит, эти треугольники равны по общему катету (PH) и гипотенузам (PA_1=PA_2=PA_3=. =PA_n) . Значит, (A_1H=A_2H=. =A_nH) . Значит, точки (A_1, A_2, . A_n) находятся на одинаковом расстоянии от точки (H) , следовательно, лежат на одной окружности с радиусом (A_1H) . Эта окружность по определению и есть описанная около многоугольника (A_1A_2. A_n) .

2) Докажем, что из ((b)) следует ((c)) .

Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H. PA_nH) прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, (angle PA_1H=angle PA_2H=. =angle PA_nH) .

3) Докажем, что из ((c)) следует ((a)) .

Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H. PA_nH) прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть (PA_1=PA_2=PA_3=. =PA_n) .

4) Докажем, что из ((b)) следует ((d)) .

Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то (H) – центр вписанной окружности. Проведем перпендикуляры из точки (H) на стороны основания: (HK_1, HK_2) и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ( (PH) – перпендикуляр на плоскость, (HK_1, HK_2) и т.д. – проекции, перпендикулярные сторонам) наклонные (PK_1, PK_2) и т.д. перпендикулярны сторонам (A_1A_2, A_2A_3) и т.д. соответственно. Значит, по определению (angle PK_1H, angle PK_2H) равны углам между боковыми гранями и основанием. Т.к. треугольники (PK_1H, PK_2H, . ) равны (как прямоугольные по двум катетам), то и углы (angle PK_1H, angle PK_2H, . ) равны.

5) Докажем, что из ((d)) следует ((b)) .

Аналогично четвертому пункту треугольники (PK_1H, PK_2H, . ) равны (как прямоугольные по катету и острому углу), значит, равны отрезки (HK_1=HK_2=. =HK_n) . Значит, по определению, (H) – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то (H) – центр описанной окружности. Чтд.

Следствие

Боковые грани правильной пирамиды – равные равнобедренные треугольники.

Определение

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.

Важные замечания

1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).

2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).

3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).

4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.

Определение

Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.

Важные замечания

1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть (SR) – высота.

2. Т.к. (SR) перпендикулярно любой прямой из основания, то (triangle SRM, triangle SRP) – прямоугольные треугольники.

3. Треугольники (triangle SRN, triangle SRK) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.

Теорема

Объем пирамиды равен трети произведения площади основания на высоту пирамиды: [V_ >=dfrac13 S_ >cdot h]

Следствия

Пусть (a) – сторона основания, (h) – высота пирамиды.

1. Объем правильной треугольной пирамиды равен (V_ >=dfrac a^2h) ,

2. Объем правильной четырехугольной пирамиды равен (V_ >=dfrac13a^2h) .

3. Объем правильной шестиугольной пирамиды равен (V_ >=dfrac a^2h) .

4. Объем правильного тетраэдра равен (V_ >=dfrac a^3) .

Теорема

Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.

Определение

Рассмотрим произвольную пирамиду (PA_1A_2A_3. A_n) . Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида ( (PB_1B_2. B_n) ), а другой называется усеченная пирамида ( (A_1A_2. A_nB_1B_2. B_n) ).