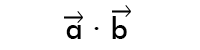Отражение вектора относительно оси

Для описания произвольного перемещения фигуры на плоскости необходимо рассмотреть несколько простейших движений, таких как параллельный перенос, поворот относительно оси и зеркальное отражение относительно оси и точки (полюса), потому что любое сложное движение всегда можно представить как совокупность простых движений.

Параллельный перенос
Параллельный перенос на вектор переносит точку M(x,y) в точку M'(x’,y’). При этом координаты точек будут изменяться на величину проекции вектора параллельного переноса на соответствующую ось

При параллельном переносе отрезок перемещается параллельно самому себе, его длина и ориентация не изменяется (рис.1).

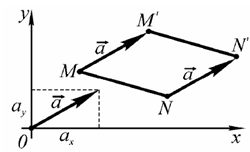
Рис.1. Параллельный перенос

Поворот
Поворот точки вокруг координатной оси против часовой стрелки на угол χ (рис. 2а) изменяет координаты точки таким образом, что расстояние от точки до начала координат не изменяется:
x′ = x cosχ − y sinχ,
y′ = x sinχ + y cosχ. (2)

При повороте отрезок не изменяет своей длины, а также не изменяются углы между совместно поворачиваемыми отрезками (рис. 2а).
Если необходимо выполнить поворот относительно произвольной точки, несовпадающей с началом координат, то сначала выполняется параллельный перенос полюса и поворачиваемого объекта на вектор a , при котором полюс совпадет с началом координат. Затем выполняется поворот, а затем параллельный перенос на вектор (- a ) (рис. 2б).

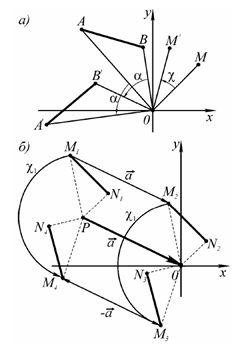
Рис.2. Поворот точки и отрезка

Отражение
Зеркальное отражение относительно оси абсцисс (рис. 3) приведет к тому, что координата x точки не меняется, а координата y меняет знак на противоположный
x’ = x, y’ = — y . (3)
При отражении относительно оси ординат знак меняется у координаты x , а у координаты y знак не изменяется
x’ = — x, y’ = y . (4)
Отражение относительно начала координат изменяет знаки на противоположные у обеих координат:
x’ = — x, y’ = — y . (5)
В том случае, если отражение производится относительно произвольной оси, то до выполнения отражения необходимо будет выполнить параллельный перенос объекта и оси на вектор a так, чтобы ось отражения совпала с одной из координатных осей, затем выполнить отражение, а после этого выполнить параллельный перенос на вектор (− a ).
При отражении относительно произвольного полюса вначале выполняется параллельный перенос, совмещающий полюс с началом координат, затем отражение относительно начала координат и после этого параллельный перенос для возврата полюса в первоначальное положение.

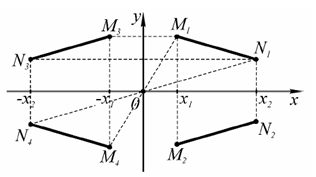
Рис.3. Отражение относительно оси и полюса.

Масштабирование и деформация
Кроме перемещений объекта по поверхности его можно деформировать. В случае если деформация будет пропорциональной, то ее можно рассматривать как масштабирование объекта. При деформации объекта координаты его точек изменяются на некоторую константу
x’= αx, y’ = βy . (6)

Если α=β, то деформация будет пропорциональной (масштабирование (рис.4)). Если константы α и β будут положительными, то производится только деформация, а если отрицательными, то кроме деформации происходит еще и отражение.

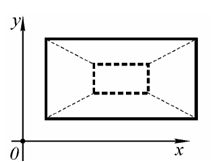
Рис.4. Масштабирование прямоугольника

Видео:Матрица поворотаСкачать

Двумерные преобразования

Видео:Построение проекции вектора на осьСкачать

ТЕМА 2. ДВУМЕРНЫЕ ПРЕОБРАЗОВАНИЯ

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

2.1. Общие замечания

В компьютерной графике, наряду с соответствующими алгоритмами рисования, важно иметь математический аппарат, позволяющий редактировать изображение, т. е. осуществлять его преобразование (модификацию) в соответствии с требованиями решаемой задачи. Необходимо уметь производить с графическими объектами (точками, отрезками прямых, плоскими и объемными фигурами) такие операции, как масштабирование (в том числе пропорциональное), сдвиги, симметричные отражения (относительно точки, линии, плоскости), повороты (например, относительно какой-либо точки или линии), перемещения и т. п. Подобные действия и их комбинации обычно реализуются с помощью матричных операций с данными. Краткие сведения об основах матричных преобразований, используемых при формировании двумерных сцен, приведены ниже (в рамках данной темы). Аналогичные преобразования при формировании объемных сцен кратко рассмотрены в следующей теме.

Видео:§4 Проекция вектора на осьСкачать

2.2. Простые преобразования точек

Точка P на плоскости однозначно определяется двумя своими координатами (x, y). В соответствие ей можно поставить матрицу-строку размером 1´2 вида (сначала будем использовать именно такое отображение точки). Следует заметить также, что точка может задаваться и соответствующей матрицей-столбцом размером 2´1. В любом случае матрицу, определяющую положение точки, часто называют координатным вектором или вектором положения.

Большинство из перечисленных выше элементарных преобразований по отношению к точке можно реализовать путем умножения матрицы на матрицу общего преобразования размером 2´2 вида :

,

где , – координаты точки P*, являющейся результатом преобразования точки P, причем .

Рассмотрим некоторые специальные случаи.

Умножение исходной матрицы на единичную 2´2 матрицу (a = d = 1, b = c = 0)

не приводит к каким-либо изменениям; поэтому подобную единичную матрицу часто называют матрицей тождественного преобразования.

– происходит так называемое локальное масштабирование (растяжение при |a| > 1 или сжатие при 0 1 или сжатие при 0 0 происходит отражение относительно оси y, при a > 0, d 1, происходит равномерное расширение, т. е. увеличение исходной фигуры, если же 0 0 осуществляет непропорциональное локальное масштабирование; неравномерное расширение и сжатие возникают в зависимости от значений (в рассматриваемом случае – положительных) a и d, которые могут быть больше или меньше, чем 1, независимо друг от друга.

Видео:§35 Формулы поворота координатных осейСкачать

2.7. Комбинированные преобразования

При модификации графического объекта часто требуется не одно простое его преобразование, а несколько последовательно проведенных преобразований. В этом случае исходную матрицу (составленную из координат точки, концов отрезка или вершин многоугольника) можно умножить на матрицу первого преобразования, полученный результат – на матрицу второго преобразования и т. д. Конечный результат будет определяться выражением

,

где – матрица n-го преобразования, n = 1, 2, …, N.

При подобных действиях следует учитывать то обстоятельство, что операция умножения матриц не является коммутативной (т. е. в общем случае ), и следует строго соблюдать порядок (последовательность) выполнения преобразований (операций умножения).

Вместе с тем, для матриц справедлив ассоциативный закон: . Поэтому для достижения того же результата можно поступить иначе: отдельные преобразования предварительно комбинировать, т. е. рассчитать матрицу полного преобразования (такую матрицу называют также композицией преобразований), и затем применить ее для преобразования исходной матрицы –

.

Продемонстрируем оба возможных подхода к комбинированному преобразованию на простом примере. Пусть требуется исходную фигуру – например, треугольник F (рис.2.8), координаты вершин которого сведены в 3´2 матрицу – повернуть на 90° вокруг точки начала координат и затем полученную промежуточную фигуру симметрично отразить относительно прямой у = – x. Первому преобразованию соответствует матрица , а второму – матрица . Осуществим последовательно соответствующие умножения:

;

очевидно, что первое умножение приводит к промежуточному результату – треугольнику F¢ (рис.2.8), второе – к конечному результату – треугольнику F* (рис.2.8).

Используем другой возможный путь комбинированного преобразования: рассчитаем матрицу полного преобразования

и умножим на нее исходную матрицу

;

результат – треугольник F* (рис.2.8) – в точности совпадает с предыдущим.

Отметим здесь, что приведенный пример очень прост: выполняются два тривиальных преобразования, результат которых можно было бы получить с помощью единственного отражения (относительно оси y). Однако он иллюстрирует изложенные выше общие положения, связанные с комбинированными преобразованиями. Далее мы будем иметь возможность познакомиться с более сложными вариантами таких преобразований.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

2.8. Однородные координаты

Ранее было замечено, что использование двумерных координатных векторов, отображающих точки на плоскости, в совокупности с матрицей общего преобразования размером 2´2 накладывает ряд ограничений на модификацию объектов. В первую очередь, эти ограничения обусловлены невозможностью применения преобразования координат. Существенно расширить возможности модификации позволяет использование однородных координат для отображения точек и, соответственно, матрицы общего преобразования размером 3´3.

Однородные координаты точки P (x, y) на физической плоскости xy представляют собой тройку чисел x¢, y¢, h; первые два из них связаны с реальными координатами точки соотношениями x¢ = hx и y¢ = hy, а h – это некоторое вещественное число (отметим, что случай h = 0 является особым и будет рассмотрен ниже). Однородным координатам точки можно поставить в соответствие трехмерный координатный вектор (вектор положения) – матрицу размером 1´3 вида . Очевидно, что при таком подходе каждую точку можно связать с бесконечным множеством наборов однородных координат и, соответственно, координатных векторов вида . Вместе с тем, для точки имеется лишь один набор однородных координат со значением h = 1; ему соответствует вектор положения вида . В компьютерной графике для отображения точек (за исключением точек бесконечности, см. далее) используются координатные векторы именно такого вида.

Применяя к вектору положения исходной точки матрицу общего преобразования размером 3´3 вида , получаем:

.

Данный результат практически идентичен тому, который был получен при умножении координатного вектора на матрицу общего преобразования размером 2´2 (см. выше). Выражения для координат и преобразованной точки в обоих случаях полностью совпадают. Следовательно, использование однородных координат совместно с матрицей общего преобразования вида позволяет осуществить все те преобразования точек, отрезков и многоугольников, о которых шла речь выше (это и происходит при реальной обработке графических объектов). Задавая соответствующие значения a, b, c и d, можно реализовать тождественное преобразование, операции локального масштабирования, отражения, сдвига и поворота, аналогичные уже рассмотренным. Однако, все они, по-прежнему, будут осуществляться относительно точки начала координат.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

2.9. Перемещение

Исследуем теперь дополнительные возможности, открывающиеся при новом подходе к преобразованиям. Проведем следующую матричную операцию:

;

полученный результат можно трактовать двояко: с одной стороны, можно считать, что операция привела к перемещению исходной точки вдоль осей x и y соответственно на m и n в исходной системе координат x0y (рис.2.9а); с другой стороны, можно полагать, что точка осталась на месте, а произошло преобразование координат – новая система координат x*0*y* сдвинута относительно исходной на – m вдоль оси x и на – n вдоль оси y (рис.2.9б).

В любом случае, выяснилось, что элементы m и n матрицы преобразования размером 3´3 являются коэффициентами перемещения в направлениях x и y соответственно. И не менее важный вывод из приведенного примера – теперь каждая точка плоскости, в том числе начало координат, может быть преобразована.

Видео:Урок 9. Проекции вектора на координатные осиСкачать

2.10. Поворот вокруг произвольной точки

Имея более мощный, чем ранее, математический аппарат можно реализовать и такое преобразование. Последовательность действий при этом может быть следующей:

§ объект преобразования перемещается таким образом, чтобы точка, относительно которой совершается поворот, попала в начало координат;

§ выполняется поворот объекта на требуемый угол вокруг точки начала координат;

§ осуществляется обратное перемещение объекта так, чтобы точка центра вращения возвратилась на исходное место.

Применительно координатному вектору точки подобная операция поворота вокруг точки с координатами (m, n) на произвольный угол q реализуется следующими матричными преобразованиями:

;

комбинируя три матрицы преобразования, получаем

.

Приведем простой пример рассмотренной операции: поворот отрезка L (рис.2.10), заданного однородными координатами его концов и , на 90° в положительном направлении (против часовой стрелки) вокруг точки с координатами (4, 5 ). Обобщая предыдущее выражение на случай преобразования отрезка, запишем (после подстановок в матрицу преобразования конкретных значений и расчета входящих в нее коэффициентов)

;

результат преобразования – отрезок L* (рис.2.10).

Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

2.11. Отражение относительно произвольной прямой

В разделе 2.5 обсуждались случаи отражения относительно ряда характерных прямых, проходящих через точку начала координат. Рассмотрим теперь более сложное преобразование – симметричное отражение объекта относительно произвольной прямой линии, причем не проходящей через начало координат. Используемый теперь подход позволяет достичь этого преобразованием, включающим пять последовательных операций:

§ перемещение объекта преобразования вдоль оси x или y таким образом, чтобы линия, относительно которой он отражается, прошла через начало координат;

§ поворот объекта относительно точки начала координат до совпадения линии, относительно которой он отражается, с одной из координатных осей;

§ симметричное отражение объекта относительно данной координатной оси;

§ обратный поворот объекта относительно точки начала координат (на тот же угол, что и во втором пункте, но в обратном направлении);

§ обратное перемещение объекта вдоль оси x или y (на то же расстояние, что и в первом пункте, но в обратном направлении).

В матричном виде полное преобразование, представляющее собой комбинацию пяти преобразований, можно записать так:

,

где – матрица перемещения, – матрица поворота вокруг начала координат, – матрица отражения относительно соответствующей координатной оси, и – матрицы, обратные матрицам соответственно и .

Приведем конкретный пример: симметричное отражение треугольника F (рис.2.11а), координатные векторы вершин которого представляются как , и , относительно прямой линии . Для того, чтобы линия прошла через точку начала координат, можно осуществить перемещение вдоль оси y на – 2 единицы; поворот относительно начала координат на – arctg 0,5 = – 26,57 ° приведет к тому, что линия совпадет с осью x; матрица отражения относительно оси x очевидна; обратный поворот и обратное перемещение осуществляются матрицами, обратными матрицам второго и первого преобразований. Композиция преобразований будет иметь вид:

;

реализуя полное преобразование, получим:

;

рис.2.11б, в, г, д иллюстрируют различные этапы промежуточных преобразований в случае последовательного их применения к исходной матрице, а рис.2.11е – конечный результат (который, вообще говоря, получен одной матричной операцией после расчета матрицы полного преобразования) – треугольник F*.

Видео:Видеоурок "Преобразование координат"Скачать

2.12. Проецирование в однородных координатах

Матрицу общего преобразования для трехмерных координатных векторов, используемых при двумерных преобразованиях, в общем виде можно представить так:

.

Ранее было установлено, как входящие в нее коэффициенты a, b, c, d, m и n влияют на соответствующие преобразования. Остальным трем коэффициентам в предыдущих разделах присваивались вполне определенные значения ( p = q = 0, s = 1), и они, по сути дела, не принимали участия в преобразованиях. Координатные векторы преобразованных точек всегда имели вид , т. е. число h (см. раздел 2.8) тождественно принимало единичное значение. Геометрически это можно трактовать как ограничение преобразований физической плоскостью h = 1 в трехмерном пространстве xyh. Вместе с тем, при других значениях коэффициентов p, q и s они также могут участвовать в преобразованиях.

Рассмотрим сначала, к какому эффекту приведут ненулевые значения коэффициентов p и q. Запишем следующее выражение:

;

данное преобразование привело к тому, что точка (x, y), которой изначально ставился в соответствие координатный вектор вида , преобразована в точку, которой ставится в соответствие координатный вектор вида , где x¢ = x, y¢ = y, ; с геометрической точки зрения полученный результат интерпретируется следующим образом: в трехмерном пространстве xyh конец P (рис.2.12) координатного вектора исходной точки принадлежит плоскости h = 1, а конец P¢ координатного вектора преобразованной точки – плоскости (причем в данном конкретном случае две другие компоненты однородных координат и соответствующего координатного вектора остаются неизменными).

Однако, как отмечалось ранее, в компьютерной графике используют векторы положения только вида . Поэтому, когда какое-либо преобразование приводит к результату с h ≠ 1 (и, кстати, с h ≠ 0), этот результат нормализуют, т. е. приводят к требуемому виду путем деления всех трех составляющих однородных координат на величину h. В рассматриваемой задаче окончательный результат преобразования будет иметь вид

;

геометрически такой же результат, а именно точку P* (рис.2.12), можно получить путем проецирования точки P¢, принадлежащей плоскости h ≠ 1, на плоскость h = 1 по лучу, соединяющему точку P¢ с началом координат.

Нетрудно заметить, что при h > 1 (как на рис.2.12) координаты x* и y* преобразованной точки пропорционально уменьшаются (в h раз) по сравнению теми же координатами исходной точки; при h 1 имеет место равномерное расширение, при 0 1 – равномерное сжатие, если 0 0, на положительной полуоси x, при условии, что x 0 положительной полуоси y, при y 0 – в первом квадранте координатной плоскости xy, при x = y 0, y 0 – во втором ее квадранте.

Видео:A.7.23+ Симметрия и отражениеСкачать

Скалярное произведение в разработке игр: проекции и прыгающие мячики в Unity ⛹

Видео:Векторы и действия над ними, проекция вектора на координатные оси. Практическая часть. 9 класс.Скачать

furry.cat

Скалярное произведение – простой, но чрезвычайно полезный математический инструмент. Он кодирует отношение между величинами и направлениями двух векторов в единственное скалярное значение. Его можно использовать для вычисления проекции, отражения, расчета тени и постановки освещения. Из этого руководства вы узнаете:

• Геометрический смысл скалярного произведения.
• Как спроецировать один вектор на другой.
• Как измерить размер объекта вдоль произвольной оси.

• Как отразить вектор относительно плоскости.
• Как создать эффект отскока мяча от наклонной поверхности.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Скалярное произведение

Представьте два вектора a и b . Вектор характеризуется только направлением и величиной (длиной), поэтому не имеет значения, в каком месте плоскости он расположен. Допустим, оба вектора начинаются в одной точке:

a и b , выходящие из одной точки плоскости» data-src=»https://media.proglib.io/posts/2020/04/04/182e211c01704ab48d14f469d9838df4.png» > Два вектора a и b , выходящие из одной точки плоскости

Проекцию одного вектора на другой можно представить как отбрасывание тени от первого вектора в направлении, перпендикулярном второму:

Проекция одного вектора на другой

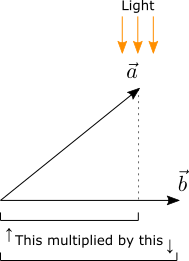
Как вы знаете, операция вычисления произведения векторов записывается так:

Далее в статье мы будем использоваться запись a * b .

Если между векторами острый угол, то длина проекции будет положительной величиной, если больше – то отрицательной.

Если b – единичный вектор, то величина проекции a на b – это просто произведение a * b .

Видео:7 2 Матрица линейного оператораСкачать

Вычисление скалярного произведения через косинус угла

На схеме изображен прямоугольный треугольник. Угол между векторами a и b равен θ .

Два вектора образуют прямоугольный треугольник

Для начала требуется рассчитать величину проекции вектора a на вектор b – это нижний катет в нарисованном нами треугольнике. Длину катета стороны можно найти, умножив длину гипотенузы треугольника на косинус прилежащего угла.

a на вектор b – это катет прямоугольного треугольника» data-src=»https://media.proglib.io/posts/2020/04/04/c4a332573e7bdc88dcc72dddf457044d.png» > Проекция вектора a на вектор b – это катет прямоугольного треугольника

Итак, длина проекции равна произведению модуля вектора a на косинус угла θ . Скалярное произведение можно выразить следующим образом:

Формула вычисления скалярного произведения через косинус

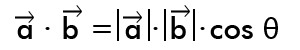
Эта формула лишний раз подтверждает, что порядок умножения не важен – в результат входят беззнаковые длины обоих векторов. Если оба вектора – единичные, правая часть формулы упрощается до cos(θ) . А если угол равен 90° (векторы перпендикулярны), то их произведение равно 0 .

Если угол острый (меньше 90°), результат будет положительным, так как косинус такого угла больше 0. Аналогично для тупого угла получится отрицательный результат. Таким образом, знак скалярного произведения дает нам некоторое представление о направлениях векторов.

Функция косинуса монотонно убывает на промежутке от 0 до 180° (от 1 до -1 ). Следовательно, чем ближе направления двух векторов, тем больше их скалярное произведение и наоборот.

• Направления совпадают, угол θ равен 0°, произведение равно |a| * |b| .
• Направления противоположны, угол θ равен 180°, произведение – -1* |a| * |b| .

Видео:Физика 9 класс (Урок№28 - Отражение света. Плоское зеркало.)Скачать

Вычисление скалярного произведения через компоненты векторов

Если наши векторы расположены в 3D-пространстве и имеют по три координаты каждый, не совсем понятно, где тот угол, косинус которого нужно вычислить. К счастью, существует другой способ расчета скалярного произведения – без всякой тригонометрии! Для начала нужно разложить каждый вектор на компоненты:

Разложение векторов на компоненты

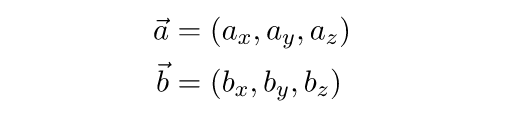
Намного проще и без всяких косинусов! В Unity есть встроенный метод Vector3.Dot для вычисления скалярного произведения двух векторов:

Его реализация выглядит следующим образом:

Нам известно, как найти длину вектора по его координатам:

Но ее можно выразить и через скалярное произведение вектора на себя:

Вернемся к формуле a * b = |a| * |b| * cos θ . При известных длинах векторов мы можем вычислить угол между ними с помощью функции арккосинуса:

Вычисление величины угла между векторами

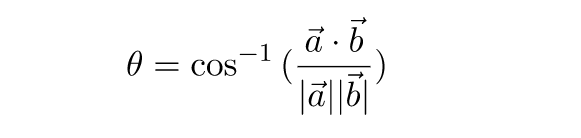
Если оба вектора являются единичными, мы можем упростить формулы:

Упрощенные формулы для единичных векторов

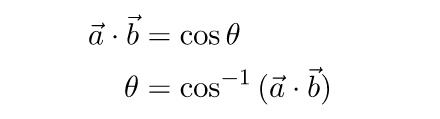
Видео:Матрица линейного оператораСкачать

Проекция вектора

Теперь, когда нам известно геометрическое значение скалярного произведения векторов (произведение длины со знаком первого проецируемого вектора и длины второго вектора), мы можем перейти к практическому применению этого знания. Например, спроецируем один вектор на другой.

Пусть вектор с = project ba – это проекция вектора a на вектор b .

Вектор c – проекция вектора a на вектор b

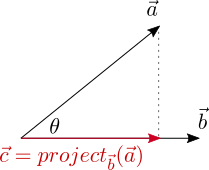
Возьмем единичный вектор в направлении вектора b . Он будет равен b / |b| . Если мы возьмем величину проекции a на b со знаком и умножим на этот единичный вектор, то получим вектор c . Cкалярное произведение a * b – это результат умножения длины b на длину проекции a на b . Отсюда получаем, что длину c со знаком можно найти, разделив скалярное произведение a * b на длину b :

Вычисление длины проекции одного вектора на другой

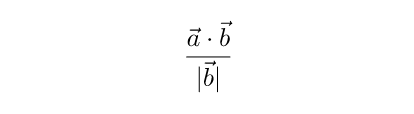
Умножив полученное значение на единичный вектор b / |b| , получаем формулу для нахождения проекции вектора:

Вычисление проекции одного вектора на другой

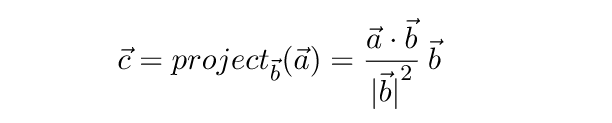
Вспомним теперь, что квадрат длины вектора равен его скалярному произведению на самого себя, и перепишем формулу:

Вычисление проекции одного вектора на другой

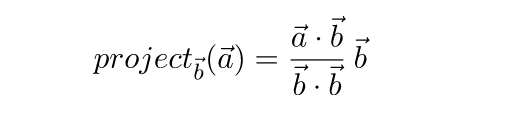
Если b – единичный вектор, то можно упростить еще больше:

Вычисление проекции вектора на единичный вектор

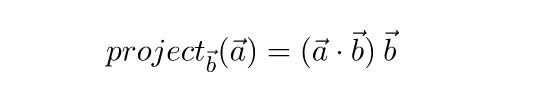
В Unity для вычисления проекции одного вектора на другой есть специальная функция Vector3.Project :

Вот так выглядит ее реализация:

Следует остерегаться возможного вырожденного случая, когда вектор, на который происходит проекция, – нулевой или имеет малую величину. При этом произойдет численный «взрыв» из-за деления на 0 или близкое к нему значение. Один из способов решить проблему – заранее вычислять величину вектора и при необходимости использовать резервный вариант (единичный вектор).

Видео:Поляризация света и закон МалюсаСкачать

Упраженение #1. Линейка

В качестве упражнения для закрепления знаний о векторной проекции сделаем линейку, которая измеряет размер объекта вдоль произвольной оси.

Линейка характеризуется базовой позицией (точка) и осью (единичный вектор):

Как спроецировать какую-либо точку ( Point ) на линейку? Прежде всего, найдем относительный вектор от базовой позиции линейки ( Base ) до этой точки. Затем спроецируем его на ось линейки ( Axis ). Проекция точки ( Projection ) – это базовое положение линейки, смещенное на проекцию относительного вектора.

Проекция точки на линейку

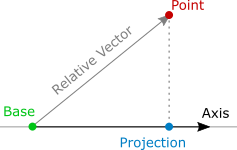
Промежуточное значение relativeDot в коде отражает, насколько далеко проекция точки находится от базового положения линейки – в направлении оси линейки, если она положительная, или в противоположном направлении, если отрицательная.

Чтобы найти размер объекта вдоль оси линейки, нужно провести такие измерения для каждой вершины меша (Mesh) и найти минимальное и максимальное значение. Ответ будет равен разнице между ними.

Видео:Проекция вектора на ось.Скачать

Отражение вектора

Еще одно практическое применение скалярного произведения – отражение вектора относительно плоскости. Рассмотрим вектор v и плоскость с нормальным вектором (перпендикуляром) n .

Отражение вектора v от плоскости

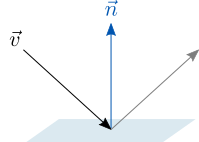
Мы можем разложить отражаемый вектор на параллельную и перпендикулярную к плоскости составляющие:

Разложение отражаемого вектора на составляющие

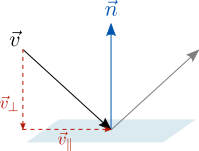
Сам вектор является суммой параллельной и перпендикулярной составляющих:

Разложение отражаемого вектора на составляющие

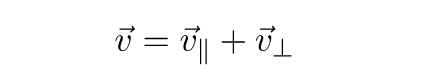
Перпендикулярный компонент, как вы уже догадались – это проекция вектор на нормаль плоскости. Параллельный компонент можно получить вычитанием этой проекции из самого вектора:

Получение параллельного плоскости компонента вектора

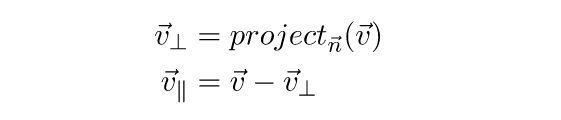
Теперь, чтобы получить искомый отраженный вектор, нужно перевернуть перпендикулярную составляющую и прибавить ее к параллельной:

Получение отраженного от плоскости вектора

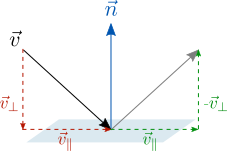
Параллельный компонент можно заменить разностью самого вектора и перпендикулярной составляющей, тогда получим следующий вид формулы:

То есть разность самого вектора и его удвоенной проекции на нормаль плоскости.

В Unity, конечно же, есть встроенная функция для расчета отраженного вектора – Vector3.Reflect :

Так выглядит реализация согласно первой выведенной нами формуле:

Видео:Симметричное рисование в иллюстратореСкачать

Упражнение #2. Отскок мяча от наклонной плоскости

Теперь, когда мы знаем все об отражении вектора от плоскости, можно переходить на следующий уровень сложности. Попробуем сымитировать движение мяча, отскакивающего от склона.

Для моделирования траектории движения шара под действием силы тяжести мы будем использовать метод Эйлера.

Чтобы определить, когда мяч ударяется о склон, нужно как-то определить момент, когда мяч проникает в плоскость.

Сфера может быть определена центром ( C ) и радиусом ( R ). Плоскость определяется нормальным вектором ( n ) и точкой на плоскости ( P ). Вектор от P до С обозначим u .

Сфера и плоскость

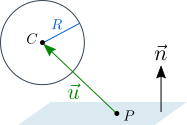
Если сфера НЕ проникает в плоскость, перпендикулярный плоскости компонент вектора u , должен иметь то же направление, что и вектор n , а также длину не менее R .

Перпендикулярный плоскости компонент вектора

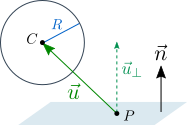
Другими словами, сфера не проникает в плоскость, если скалярное произведение векторов u и n больше R . В противном случае величина проникновения составляет R – u * n , и положение сферы нужно исправить.

Чтобы это сделать, можно просто переместить сферу в направлении нормали плоскости n на величину проникновения. Это лишь приближенное решение, которое не является физически правильным, но для упражнения оно хорошо подходит.

Добавим логику для коррекции позиции:

Нам также нужно отразить скорость, с которой движется сфера, относительно наклона, чтобы она правильно отскакивала.

Эта анимация демонстрирует идеальное отражение и выглядит неестественной. Мы ожидаем, что с каждым отскоком скорость мяча будет уменьшаться.

Это поведение обычно моделируется значением реституции (восстановления) между двумя сталкивающимися объектами. При 100% реституции мяч идеально отскакивает от плоскости. При 50% – величина перпендикулярной к плоскости составляющей скорости мяча будет уменьшена вдвое.

Величина реституции – это отношение величин перпендикулярного к плоскости компонента скорости мяча до и после отскока.

Вот пересмотренный с учетом коэффициента восстановления скорости вариант функции отражения:

Вот так выглядит обновленная функция SphereVsPlane :

Логика корректировки позиции заменяется логикой полноценного отскока:

Теперь мы можем устанавливать разные коэффициенты реституции для разных шариков:

Видео:Ортогональная проекция вектора на прямую и вектора на ось. Теоремы о проекцияхСкачать

Заключение

Мы ответили на все вопросы, заданные в начале этого руководства.

• Скалярное произведение двух векторов – это произведение проекции первого вектора на второй (с учетом знака) и модуля второго вектора.
• Существует две формулы вычисления скалярного произведения: через косинус угла и через компоненты векторов.
• Скалярное произведение имеет множество полезных практических применений. Например, оно позволяет рассчитать проекцию вектора на другой вектор.
• С помощью скалярного произведения можно найти отраженный от плоскости вектор. На этой основе строятся различные физические модели, например, имитация отскока шарика от плоскости.

Расскажите в комментариях – разрабатываете ли вы сейчас какую-нибудь игру и если да, то о чем она. Каких уроков по Unity вам не хватает?