- Ваш ответ
- решение вопроса
- Похожие вопросы
- Найдите отношение площадки правильных четырёхугольника и шестиугольника, стороны которых равны.
- Вопрос вызвавший трудности
- Ответ подготовленный экспертами Учись.Ru
- Площади четырехугольников
- Формулы для площадей четырехугольников
- Вывод формул для площадей четырехугольников
- 📹 Видео
Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Ваш ответ
Видео:Отношение площадей треугольников с равным угломСкачать
решение вопроса
Видео:Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,658
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Геометрия Найдите отношение площадей правильного треугольника, квадрата и правильного шестиугольникаСкачать

Найдите отношение площадки правильных четырёхугольника и шестиугольника, стороны которых равны.
В 5:30 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Видео:Площади треугольников с равным углом.Скачать

Вопрос вызвавший трудности
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Найдите отношение площадки правильных четырёхугольника и шестиугольника, стороны которых равны.
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Киселёва Лали Дамировна — автор студенческих работ, заработанная сумма за прошлый месяц 54 269 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.
Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.
Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
Видео:Математика ОГЭ Задание 26 Отношение площадейСкачать

Площади четырехугольников
 Формулы для площадей четырехугольников Формулы для площадей четырехугольников |
 Вывод формул для площадей четырехугольников Вывод формул для площадей четырехугольников |
 Вывод формулы Брахмагупты для площади вписанного четырехугольника Вывод формулы Брахмагупты для площади вписанного четырехугольника |
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Видео:Задание 26 Отношение площадей Треугольник ЧетырёхугольникСкачать

Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник |  | S = ab | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Параллелограмм |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Квадрат |  | S = a 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = 4r 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ромб |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Трапеция |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | S = m h | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дельтоид |  | S = ab sin φ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Произвольный выпуклый четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вписанный четырёхугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прямоугольник | ||
 | ||
 | ||
 | ||
| Параллелограмм | ||
 | ||
 | ||
 | ||
| Квадрат | ||
 | S = a 2 где | |
 | S = 4r 2 | |
 | ||
 | ||
| Ромб | ||
 | ||
 | ||
 | ||
 | ||
 | ||
| Трапеция | ||
 | ||
 | ||
 | ||
 | ||
| Дельтоид | ||
 | ||
 |  где | |
 | ||
 | ||
| Произвольный выпуклый четырёхугольник | ||
 | ||
| Вписанный четырёхугольник | ||
 | ||
| Прямоугольник |
 |
где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

где
a – сторона квадрата



Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
ha – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба



где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота


φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности


φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Видео:Отношение площадейСкачать
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
📹 Видео
9 класс, 12 урок, Теорема о площади треугольникаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Отношение площадей треугольниковСкачать
Задание 24 Отношение площадей 3 способа решенияСкачать
Геометрия 8 класс (Урок№14 - Определение подобных треугольников. Отношение площадей подобных фигур.)Скачать

Отношение площадей подобных треугольников.Скачать

#57. Отношение площадей треугольников — самые надежные отношения!Скачать

Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

Геометрия 8 класс : Отношение площадей подобных треугольниковСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

ПЛОЩАДЬ МНОГОУГОЛЬНИКА: Формула Пика, Площадь четырёхугольника, Площадь правильного шестиугольникаСкачать

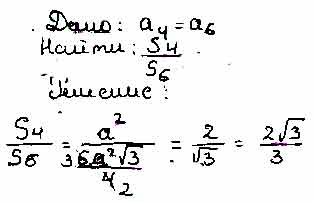






 ,
,























