Окружности s1 и s2 пересекаются в точках a и p

2019-01-19
Окружности $S_1$ и $S_2$ пересекаются в точках $M$ и $N$. Через точку $A$ окружности $S_1$ проведены прямые $AM$ и $AN$, пересекающие $S_2$ в точках $B$ и $C$, а через точку $D$ окружности $S_2$ — прямые $DM$ и $DN$, пересекающие $S_1$ в точках $E$ и $F$, причем $A, E, F$ лежат по одну сторону от прямой $MN$, а $D, B, C$ — по другую (рис.). Докажите, что если $AB=DE$, то точки $A, F, C$ и $D$ лежат на одной окружности, положение центра которой не зависит от выбора точек $A$ и $D$.

Лемма (теорема Н.И.Фусса). Пусть окружности $S_1$ и $S_2$ пересекаются в точках $M$ и $N$. Через точку $M$ проведена прямая, пересекающая $S_i$ в точке $E, S_2$ — в точке $D$, а через $N$ — прямая, пересекающая $S_i$ в точке $A, S_2$ — в точке $C$. Тогда $AE parallel CD$.

Доказательство. Мы рассмотрим случай, изображенный на рис, который соответствует условию решаемой нами задачи. В остальных случаях доказательство проводится аналогично. Из вписанных четырехугольников $angle NME$ и $NCDM$ получаем, что $angle AEM = 180^ — angle ANM = angle MNC = 180^ — angle MDC$, т. е. $angle AEM + angle MDC = 180^$, следовательно, $AE parallel CD$.

Перейдем к решению задачи, обратившись к рис.

Рассмотрим треугольники $ANB$ и $END$. Они равны, так как $AB = ED, angle NAB = angle NED, angle NBA = angle NDE$. Откуда $AN = NE$ и $BN = ND$.

Пусть $NK$ и $NL$ — диаметры $S_1$ и $S_2$ соответственно. Тогда $angle KMN = angle LMN = 90^$, т. е. точки $K, M, L$ лежат на прямой, перпендикулярной $NM$. Кроме того, $breve = breve, breve = breve$, следовательно, $angle AMK = angle DML, angle AMN = angle DMN$. Теперь из вписанных четырехугольников $AFNM$ и $DCNM$ получаем, что $angle AFN = angle DCN$, т. е.точки $A, F, C, D$ лежат на одной окружности.

Покажем, что центр этой окружности — середина отрезка $KL$. Пусть прямая $KN$ пересекает $S_2$ в точке $P$, а прямая $LN$ пересекает $S_1$ в точке $T$. Из того, что $KP perp AE (AN = NE)$ и $AE parallel CD$ (лемма) следует, что $KP perp CD$. Но $NP perp PL$, откуда $PL parallel CD$. Поэтому серединные перпендикуляры к $CD$ и $PL$ совпадают. Аналогично доказывается, что совпадают серединные перпендикуляры к $AF$ и $KT$. Осталось заметить, что эти перпендикуляры проходят через середину $KL$, так как треугольники $KPL$ и $KTL$ прямоугольные.

Замечание. Утверждение задачи остается справедливым, даже если в условии отказаться от уточнения взаимного расположения точек $A, E, F, D, B, C$.

Видео:Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Окружности S₁ и S₂ пересекаются в точках A и P. Через точку A проведена касательная AB к окружности S₁, а через точку P — прямая CD, параллельная прямой AB (точки B и C лежат на S₂, точка D — на S₁). Докажите, что ABCD — параллелограмм.

Рассмотрим случай, когда точка P лежит между точками D и C. Поскольку APCB — равнобедренная трапеция, то

ABC = PAB = ADP = 180 o — DAB.

Следовательно, AD || BC. Поэтому ABCD — параллелограмм. Аналогично для случая, когда точка P не лежит между D и C.

Видео:Касательные к окружности пересекаются в точке. Теорема и решение задач. Геометрия 7-8 классСкачать

Окружности s1 и s2 пересекаются в точках a и p

БАЗА ЗАДАНИЙ

Задание № 16. Планиметрия с доказательством.

1. Прямая, проходящая через вершину B прямоугольника ABCD перпендикулярно диагонали AC, пересекает сторону AD в точке M, равноудалённой от вершин B и D.
а) Докажите, что ∠ABM =∠DBС = 30°.
б) Найдите расстояние от центра прямоугольника до прямой CM, если BC = 9.

2. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата.
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Ответ: б) 1:3

3. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC = AP:PD.
б) Найдите площадь треугольника COD, где O— центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а BC = 6√2.
Ответ: б) 18√3

4. В треугольнике ABC точки A ₁ , B ₁ , C ₁ — середины сторон BC, AC и A B соответственно, AH— высота, ∠BAC = 60°, ∠BCA = 45°.
а) Докажите, что точки A₁, B₁, C₁, H— лежат на одной окружности.
б) Найдите A₁ H, если BC = 2√3.

5. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L— точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.
Ответ: б) √10

6. Две окружности касаются внутренним образом в точке A, причём меньшая окружность проходит через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.
а) Докажите, что прямые PQ и BC параллельны.
б) Известно, что sin ∠AOC=√15/4. Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.
Ответ: б) 1:4

7. Две окружности касаются внутренним образом в точке K, причём меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке C. Хорды KM и KN пересекают меньшую окружность в точках A и B соответственно, а отрезки KC и AB пересекаются в точке L.
а) Докажите, что CN:CM = LB:LA.
б) Найдите MN, если LB:LA = 2:3, а радиус малой окружности равен √23.
Ответ: б) 115/6

8. Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN = 4 и AM:MC = 1:3.

9. Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.

10. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N— точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.

11. В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB = 5, AC = 8.
Ответ: б) 2,88

12. Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC = ∠OBC+∠OCB.
а) Докажите, что точка H лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OHI, если ∠ABC = 55°.

13. Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB = CQ:QB = CW:WD = 3:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ = 16, QW = 12, угол PWQ— острый.
а) Докажите, что треугольник PQW— прямоугольный.
б) Найдите площадь четырёхугольника ABCD.

14. Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C ₁ , B ₁ соответственно.
а) Докажите, что треугольник АВC подобен треугольнику AB ₁ C ₁ .
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45°, B ₁ C ₁ =6 и площадь треугольника AB ₁ C ₁ в восемь раз меньше площади четырёхугольника BCB ₁ C _{1 .}

15. Дана трапеция ABCD с основаниями AD и BC. Диагональ BD разбивает её на два равнобедренных треугольника с основаниями AD и CD.
а) Докажите, что луч AC— биссектриса угла BAD.
б) Найдите CD, если известны диагонали трапеции: AC = 15 и BD = 8,5.

16. В прямоугольном треугольнике АВС с прямым углом С точки М и N – середины катетов АС и ВС соответственно, СН – высота.
а) Докажите, что прямые MH и NH перпендикулярны
б) Пусть Р – точка пересечения прямых АС и NH, а Q – точка пересечения прямых ВС и MH. Найдите площадь треугольника PQM, если АН = 12 и ВН = 3.

17. В треугольнике АВС угол АВС равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin ∠BMC если известно, что отрезок ВМ в 2,5 раза больше радиуса вписанной в треугольник окружности.
Ответ: б) 0,65

18. В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.
а) Докажите, что прямые ЕН и АС параллельны.
б) Найдите отношение ЕН:АС, если угол АВС равен 30.
Ответ: б) 3:4

19. Окружность, вписанная в треугольник KLM, касается сторон KL, LM, MK в точках A, B и C соответственно.
а) Докажите, что KC = (KL+KM-LM)/2 .

б) Найдите отношение LB:BM, если известно, что KC:CM = 3:2 и ∠ MKL = 60.
Ответ: б) 5:2

20. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.
а) Докажите, что четырёхугольник DQOH — параллелограмм.
б) Найдите AD, если ∠BAD = 75° и BC =1.
Ответ: б) 3

21. Квадрат ABCD вписан в окружность. Хорда CE пересекает его диагональ BD в точке K.
а) Докажите, что CK*CE = AB*CD.
б) Найдите отношение CK к KE, если ∠ ECD = 15.
Ответ: б) 2:1

22. В прямоугольном треугольнике ABC точки M и N – середины гипотенузы AB и катета BC соответственно. Биссектриса ∠ BAC пересекает прямую MN в точке L
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если cos ∠BAC = 7/25.
Ответ: б) 25:36

23. Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону BC.
Ответ: б) 5:4

24. На катетах AC и BC прямоугольного треугольника ABC как на диаметрах построены окружности, второй раз пересекающиеся в точке M. Точка Q лежит на меньшей дуге MB окружности с диаметром BC. Прямая CQ второй раз пересекает окружность с диаметром AC в точке P.
а) Докажите, что прямые PM и QM перпендикулярны.
б) Найдите PQ, если AM = 1, BM = 3, а Q – середина дуги MB.

25. Окружность, построенная на медиане BM равнобедренного треугольника ABC как на диаметре, второй раз пересекает основание BC в точке K.
а) Докажите, что отрезок BK втрое больше отрезка CK.
б) Пусть указанная окружность пересекает сторону AB в точке N. Найдите AB, если BK = 24 и BN = 23.

26. В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая – боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центр окружностей, пересекает основание AD в точке P. Докажите, что AP/PD = sin ∠D.
б) Найдите площадь трапеции, если радиусы окружностей равны 3 и 1.

27. В трапецию ABCD с основаниями AD и BC вписана окружность с центром O.
а) Докажите, что sin ∠AOD = sin ∠ BOS.
б) Найдите площадь трапеции, если ∠ BAD = 90, а основания равны 5 и 7.

28. Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите площадь трапеции.

💥 Видео

Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Угол между касательной и хордой | Задачи 1-10 | Решение задач | Волчкевич|Уроки геометрии 7-8 классыСкачать

ОГЭ 24 | КАК РЕШАТЬ ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО | ОКРУЖНОСТИ С ВНУТРЕННЕЙ КАСАТЕЛЬНОЙСкачать

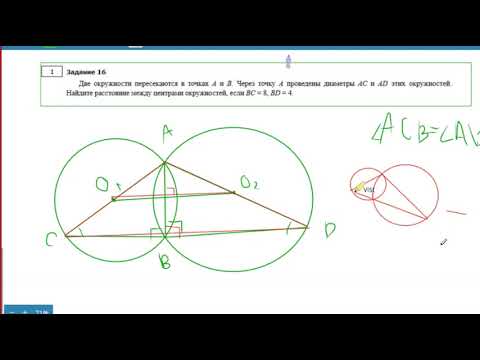
Две окружности пересекаются в точках A и B Через точку A проведены диаметры AC и AD этих окружностеСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Касательная к окружностиСкачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Почему серединные перпендикуляры пересекаются в одной точке? | Vasily mathsСкачать

ОГЭ 2022. Задание 16. Касательная, хорда, секущая. Основные теоремы для решения задач + много задачСкачать

Свойства хорд, касательных, секущих окружности I Для решения задач из ОГЭ И ЕГЭ I Часть 1Скачать

#59. Олимпиадная задача о касательной к окружности!Скачать

Окружность, касательная, секущая и хорда | МатематикаСкачать

11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать

8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Угол между хордой и касательнойСкачать