Определение высоты треугольника построение

В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Определение высоты треугольника

Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.

Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).

Обычно высота обозначается буквой h (иногда как h_a – это означает, что она проведена к стороне a).

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Высота в разных видах треугольников

В зависимости от вида фигуры высота может:

• проходить внутри треугольника (в остроугольном △);
  
• проходить за рамками треугольника (в тупоугольном △);
  
• являться одним из катетов (в прямоугольном △), за исключением высоты, проведенной к гипотенузе.
  

Видео:Построение высоты в треугольникеСкачать

Свойства высоты треугольника

Свойство 1

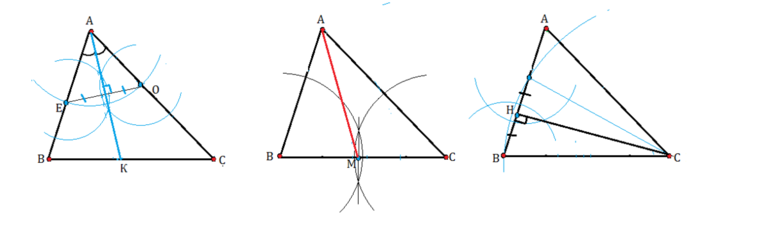
Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).

• в остроугольном треугольнике;
  
• в тупоугольном треугольнике;
  
• в прямоугольном треугольнике.
  
  Вершина A является, в т.ч., точкой пересечения высот.

Свойство 2

При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:

• △ABE∼△CBF: по двум углам (∠ABC – общий, ∠AEB и ∠CFB являются прямыми).
  
• △AFG∼△CEG: по двум углам (∠AFG и ∠CEG – прямые, ∠AGF и ∠CGE равны как вертикальные углы).
• △ABC∼△BEF: по трем равным углам (∠ABC = ∠EBF, ∠ACB = ∠BFE, ∠CAB = ∠BEF).
  
  Примечание: доказательство подобия последней пары треугольников достаточно длинное и не является целью данной статьи, поэтому подробно останавливаться на нем будем.

Свойство 3

Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.

Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.

Свойство 4

Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.

Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Высота треугольника

Средняя оценка: 4.6

Всего получено оценок: 80.

Средняя оценка: 4.6

Всего получено оценок: 80.

Почти никогда не получится определить все параметры треугольника без дополнительных построений. Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.

Видео:Высоты треугольника.Скачать

Определение

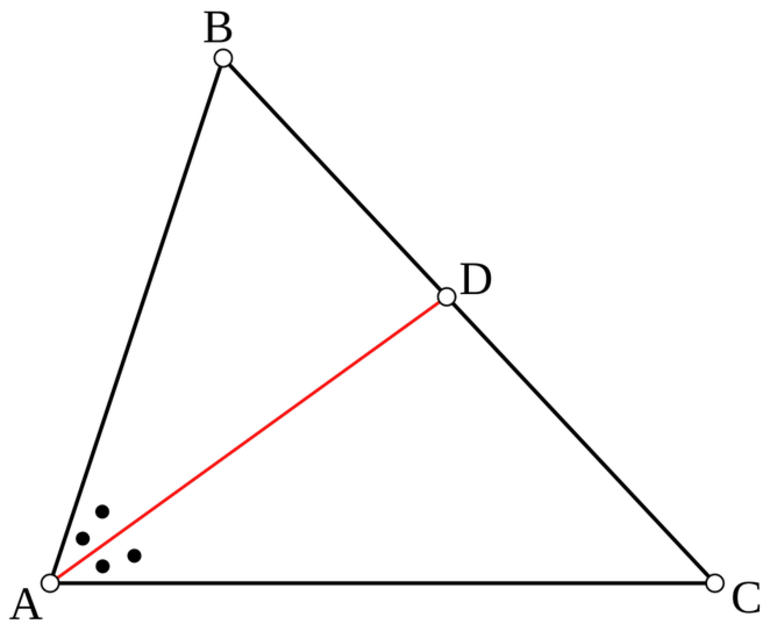
Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя отрезками составляют треугольник.

Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, нестандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.

Как правило, высоту треугольника обозначают буквой h. Также обозначается высота и в других фигурах.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Как найти высоту треугольника?

Существует три стандартных способа нахождения высоты треугольника:

Через теорему Пифагора

Этот способ применяется для равносторонних и равнобедренных треугольников. Разберем решение для равнобедренного треугольника, а потом скажем, почему это же решение справедливо для равностороннего.

Дано: равнобедренный треугольник АВС с основанием АС. АВ=5, АС=8. Найти высоту треугольника.

Рис. 2. Рисунок к задаче.

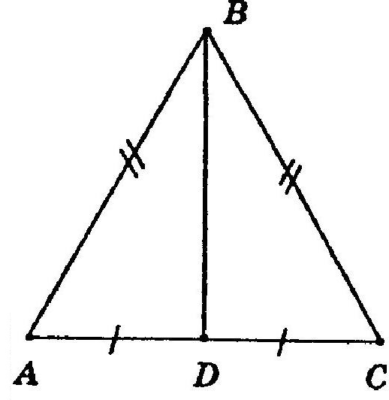
Для равнобедренного треугольника важно знать, какая именно сторона является основанием. Это определяет боковые стороны, которое должны быть равны, а так же высоту, на которую действую некоторые свойства.

Свойства высоты равнобедренного треугольника, проведенной к основанию:

• Высота совпадает с медианой и биссектрисой
• Делит основание на две равные части.

Высоту обозначим, как ВD. DС найдем как половину от основания, так как высота точкой D делит основание пополам. DС=4

Высота – это перпендикуляр, значит ВDС – прямоугольный треугольник, а высота ВD является катетом этого треугольника.

Найдем высоту по теореме Пифагора: $$BD=sqrt=sqrt=3$$

Любой равносторонний треугольник является равнобедренным, только основание у него равно боковым сторонам. То есть, можно использовать тот же порядок действий.

Через площадь треугольника

Этим способом можно пользоваться для любого треугольника. Чтобы им воспользоваться, нужно знать значение площади треугольника и стороны, к которой проведена высота.

Высоты в треугольнике не равны, поэтому для соответствующей стороны получится вычислить соответствующую высоту.

Формула площади треугольника: $$S=*bh$$, где b – это сторона треугольника ,а h – высота, проведенная к этой стороне. Выразим из формулы высоту:

Если площадь равна 15, сторона 5, то высота $$h=2*=6$$

Через тригонометрическую функцию

Третий способ подойдет, если известна сторона и угол при основании. Для этого придется воспользоваться тригонометрической функцией.

Рис. 3. Рисунок к задаче.

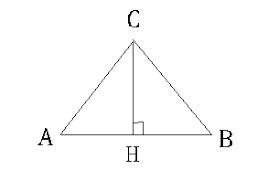
Угол ВСН=30 градусам , а сторона BC=8. У нас все тот же прямоугольный треугольник BCH. Воспользуемся определением косинуса угла прямоугольного треугольника. Косинус острого угла – это отношение прилежащего катета к гипотенузе, значит: BH/BC=cos BCH, а угол BCH равен 60 градусам, так как сумма острых углов прямоугольного треугольника равна 90 градусам.

Угол известен, как и сторона. Выразим высоту треугольника:

Значение косинуса в общем случае берется из таблиц Брадиса, но значения тригонометрических функций для 30,45 и 60 градусов – табличные числа.

Видео:17. Медианы, биссектрисы и высоты треугольникаСкачать

Что мы узнали?

Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.

Видео:Построение медианы в треугольникеСкачать

Как построить высоту треугольника — основные способы

Видео:Как найти высоту треугольникаСкачать

С применением циркуля

Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.

Способ начертить искомый отрезок:

• На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
• Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
• Иглу циркуля ставят в вершине любого угла у основания.
• Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
• Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
• Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
• Делают пометку в месте пересечения начерченных окружностей.
• Ластиком стирают лишние линии, оставляя лишь поставленную точку.
• С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
• Стирают линии, находящиеся под основанием.

Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

С помощью линейки

Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.

В остроугольном треугольнике

Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.

Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.

Правильная последовательность действий:

• Находят вершину, из которой хотят провести перпендикуляр.
• Совмещают угольник с противоположной стороной фигуры.
• Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
• Простым карандашом проводят линию, которая и будет искомым отрезком.

В тупоугольной фигуре

Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.

Порядок действий:

• Располагают чертёж так, чтобы тупой угол оказался у основания.
• Угольник прикладывают к наибольшей стороне фигуры.
• Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
• Соединяют 2 точки простым карандашом, получая искомую линию.

В прямоугольном и равнобедренном

В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.

Пошаговая инструкция:

• Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
• Вторую сторону линейки совмещают с вершиной прямого угла.
• Проводят линию, которая будет высотой.

Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.

Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:

• Линейкой замеряют длину основания.
• Эту величину делят на 2.
• Полученное значение откладывают от вершины одного из углов при основании.
• Отмечают середину стороны и соединяют её с верхней точкой фигуры.

Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.

Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.

💥 Видео

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

ПОСТРОЕНИЕ ВЫСОТЫ ТРЕУГОЛЬНИКА С ПОМОЩЬЮ ЦИРКУЛЯ. ЗАДАЧИ НА ПОСТРОЕНИЕ | ГЕОМЕТРИЯ 7 классСкачать

Построение биссектрисы в треугольникеСкачать

Медиана, высота и биссектриса треугольника. Центроид, инцентр, ортоцентр. Геометрия 7 класс.Скачать

Высота, медиана, биссектриса треугольника. Как построить в треугольнике. Геометрия 7 классСкачать

№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

№102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.Скачать

Медианы, биссектрисы и высоты треугольника | Геометрия 7-9 класс #18 | ИнфоурокСкачать

Построение биссектрисы угла. 7 класс.Скачать

Геометрия 7.Треугольники урок 6. Высота треугольника. Определение, свойства, точки пересечения высотСкачать