Задача с решением из Пособия для старшеклассников и абитуриентов по геометрии из раздела:
Треугольник: Неравенство треугольника
1 Существует ли треугольник со сторонами 1 м, 2 м и 3 м; 1,2 дм, 1 дм и 2,4 дм
РЕШЕНИЕ
1 1. В равнобедренном треугольнике одна сторона равна 25 см, а другая равна 10 см. Какая из них является основанием
РЕШЕНИЕ
2 Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 74 см, а одна из сторон равна 16 см. Найдите две другие стороны треугольника.
РЕШЕНИЕ
1 Периметр равнобедренного треугольника равен 25 см, разность двух сторон равна 4 см, а один из его внешних углов – острый. Найдите стороны треугольника.
РЕШЕНИЕ
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать
Урок геометрии в 7-м классе «Неравенство треугольника»
Разделы: Математика
Цель урока: изучить теорему о неравенстве треугольника и показать ее применение при решении задач.
Задачи:
- Образовательные:
- относительно учащихся: научиться применять свойство «неравенство треугольника» и определять несуществующие треугольники;
- относительно педагога: объяснить новую тему с первичным закреплением новых знаний; включить учеников в исследовательскую деятельность;
- показать практическое применение полученных знаний; создать условия для формирования целостной картины мира.
- Развивающие:
- развитие речи, мышления, сенсорной (восприятие внешнего мира через органы чувств) сферы личности и потребностно-мотивационной области;
- развитие умственной деятельности (выполнять операции анализа, синтеза, способность наблюдать, делать выводы, выделять существенные признаки объектов, цели и способы деятельности, выдвигать гипотезы).
- Воспитательные:
- повысить интерес к традициям края;
- развивать самостоятельность, умение работать парами;
- способствовать формированию коммуникативной компетенции.
Тип урока: урок изучения и первичного закрепления новых знаний.
Оборудование: доска, компьютер, интерактивная доска или мультимедийный проектор, презентация, учебники, рабочие тетради (Приложение 1), 14 наборов полосок из картона по 5 см, 7 см (2 шт.), 9 см, 12 см, 14 см, 16 см, таблички с треугольниками, смайлики (Приложение 2).
1. Организационный этап
2. Подготовка к основному этапу урока (обеспечение мотивации и принятия учащимися цели учебно-познавательной деятельности, актуализация опорных знаний)
– Посмотрите на рисунок, выполненный на доске. Как называется эта фигура? (Это треугольник.)
– Какая фигура называется треугольником? (Треугольник – фигура, состоящая из трех точек, не лежащих на одной прямой и трех отрезков, попарно соединяющих эти точки.)
– Что возникает в вашей памяти? Что вы можете рассказать об этом треугольнике? Если обозначить треугольник АВС, назовите большую сторону. (Ребята отвечают на вопросы учителя.)
– А почему именно эту фигуру я предложила вам вспомнить? (Будем изучать какие-то свойства треугольника.)
– Совершенно верно, сегодня мы будем изучать свойство «неравенство треугольника».
3.Усвоение новых знаний и способов действий
3.1. Постановка проблемы, выдвижение гипотезы
Еслиб только меня спросили,
Я б ответил предельно кратко,
Что не видел Земли красивей
И загадочней, чем Камчатка.
Где вулканы царапают небо,
Низвергая к подножьм лавы,
Где сплетаются быль и небыль,
И где в рост человека травы.
– Эти замечательные стихи Анатолия Старикана посвящены нашей малой родине Камчатке. Камчатка имеет свои традиции, и одной из них является ежегодное проведение Берингии.
– Ребята, а что такое Берингия? (Это ставшая традиционной гонка на собачьих упряжках, которая проводится с 1990 года.)
– Обычно Берингия проводится в марте и вместе с началом весны приходит в населенные пункты на своем пути, принося радость их обитателям. Стоит заметить, что гонка помимо состязательной составляющей, имеет еще и гуманитарное значение для жителей сел и поселков Камчатского края, где отдыхают участники гонки. Детям и школам отдаленных уголков Камчатки оказывают спонсорскую помощь.
В этом году Беригиня проходила с 7 по 21 марта.
Проблемная ситуация.
Берингия стартовала из села Эссо, и одним из пунктов остановки стал поселок Тигиль. Расстояние между этими населенными пунктами 443 км. Далее каюры отправились в поселок Оссора. На каком расстоянии от села Эссо может находиться поселок Оссора, если расстояние между поселком Тигиль и поселком Оссора 507 км?
Какую фигуру необходимо построить, чтобы решить эту проблему? (Необходимо построить треугольник.) Какова может быть длина третьей стороны? Выскажите свои гипотезы, мы проверим их в конце урока.
Ученики отвечают на вопросы учителя, строят треугольник в рабочей тетради и высказывают свои гипотезы, например, расстояние между с. Эссо и п. Оссора меньше 950 км.
- 3.2. Проведение исследования, формулирование нового свойства сторон треугольника
Основной фигурой в рассматриваемой проблеме является треугольник. Я уверена, что вы очень наблюдательны. Скажите, а где еще в повседневной жизни вам встречались треугольные формы? В архитектуре? (Знак аварийной остановки и т.д. Крыши имеют треугольную форму.)
– Вы правы. Основу крыш составляют наклонные и горизонтальные балки, которые соединены между собой и образуют треугольник.
Давайте сконструируем макеты собственных крыш. Представьте, что те полоски, которые лежат перед вами – это балки для построения крыши дома.
Исследовательская работа
– Перед вами лежат макеты сторон треугольников.
Постройте, используя эти макеты треугольники со сторонами:
В первой задаче треугольник построить легко. Во второй получился отрезок. Почему? (Т.к. три вершины лежат на одной прямой, а треугольник – это фигура, составленная из трех точек, не лежащих на одной прямой, попарно соединенных отрезками. Длина большего отрезка равна сумме длин меньших.)
– Можно ли построить треугольник в третьем случае? (В третьем случае треугольник построить нельзя, так как длина большей стороны больше суммы длин меньших сторон.)
Учитель выслушивает версии учеников. В случае затруднения можно предложить детям сравнить длину стороны, построенной первой и сумму двух других сторон треугольника.
Верная версия детей: «Если сторона, построенная первой, меньше суммы двух других сторон, то треугольник строится».
– Итак, треугольник, с какими сторонами мы смогли построить? (Треугольник со сторонами 7, 12, 9.)
AB
| П | Р | И | Т | Ч | И | Н |
5. Первичная проверка понимания и закрепление знаний
– Выберите, какие треугольники не существуют?
(Ученики работают самостоятельно, один человек работает у доски, потом проверка.)
Ответ: не существуют треугольники с номерами 3, 5, 6.
– Ребята, что вы заметили? Как быстро применить теорему о неравенстве треугольника?
(Высказывают свои версии.) – Сумма двух сторон, должна быть больше третьей стороны. Например, 10 + 3 > 5, но треугольник построить нельзя, почему? (Так как 3 + 5 18.04.2012
Видео:Неравенства треугольника. 7 класс.Скачать
Неравенство треугольника
теория по математике 📈 планиметрия
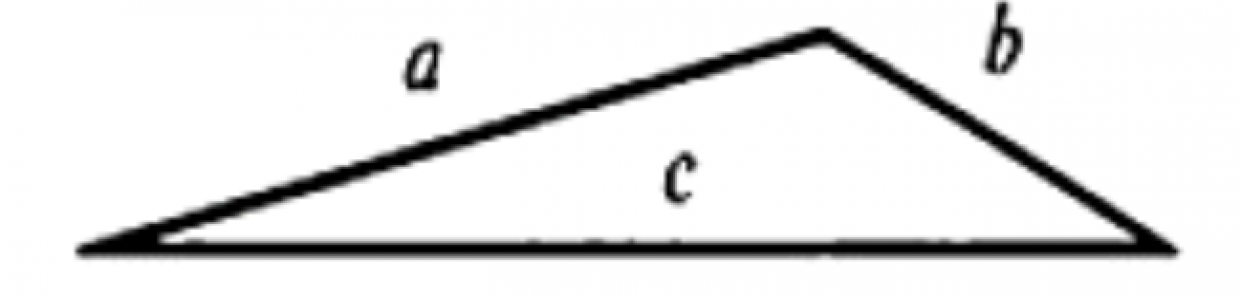
Каждая сторона любого треугольника меньше суммы двух других сторон.
На данном рисунке показан произвольный треугольник, стороны которого обозначены для удобства буквами а, b, c. Так, в соответствии с неравенством треугольника:
Можно ли построить треугольник со сторонами 12, 18 и 23 см?
Для ответа на вопрос данной задачи нужно проверить каждую сторону на верность неравенства: 12
Существует ли треугольник со сторонами 19, 21 и 11 см?
Для ответа на вопрос данной задачи нужно также проверить каждую сторону на верность неравенства: 19 Даниил Романович | Просмотров: 877 | Оценить:
🔍 Видео
Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать
Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать
Признаки равенства треугольников. Практическая часть. 7 класс.Скачать
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Неравенства треугольника. Практическая часть. 7 класс.Скачать
Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать
7 класс, 34 урок, Неравенство треугольникаСкачать
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать
7 класс, 15 урок, Первый признак равенства треугольниковСкачать
Треугольники. Практическая часть - решение задачи. 7 класс.Скачать
✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать
Геометрия. Задачи. Неравенство треугольника.Скачать
РЕШЕНИЕ ЗАДАЧИ ПО ТЕМЕ «НЕРАВЕНСТВО ТРЕУГОЛЬНИКА». Задачи | ГЕОМЕТРИЯ 7 классСкачать
Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать
Признаки равенства треугольников. 7 класс.Скачать
Первый признак равенства треугольников. 7 класс.Скачать
Задачи на доказательство по геометрии. Первый признак равенства треугольников.Скачать
первый признак равенства треугольников. Задачи по готовым чертежам, рисункам. 7 классСкачать
