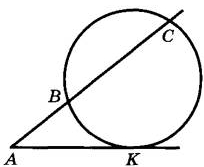
Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке К. Другая прямая пересекает окружность в точках В и С, причём АВ = 4, BС = 12. Найдите АК.
Источник: ОГЭ Ященко 2022 (50 вариантов)
Найдём АС:
АС = АВ + ВС = 4 + 12 = 16
По теореме о секущей и касательной (подробно о ней здесь):
Если из одной точки (А) к окружности проведены секущая (АС) и касательная (АК), то произведение всей секущей (АС) на ее внешнюю часть (АВ) равно квадрату отрезка касательной (АК).
АС·АВ = АК 2
16·4 = АК 2
64 = АК 2
АК = √64 = 8
Ответ: 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Касательная к окружности
Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
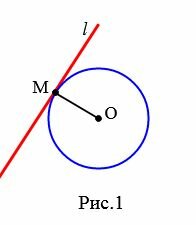
На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.
 |
Видео:Прямая касается окружности в точке K ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Свойство касательной
Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.
Доказательство. Пусть l касательная к окружности с центром O и M − точка касания прямой и окружности (Рис.1). Докажем, что ( small l ⊥ OM .)
Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.
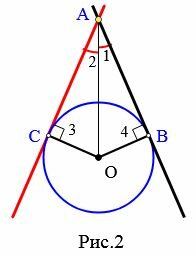
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.
 |
Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.
Доказательство. Рассмотрим рисунок 2. По теореме 1 касательные AC и AB перпендикулярны радиусам OC и OB, соответственно. Тогда углы 3 и 4 прямые, а треугольники ACO и ABO, прямоугольные. Эти треугольники равны по катету (OC=OB) и гипотенузе (сторона AO− общая) (подробнее см. в статье Прямоугольный треугольник. Онлайн калькулятор). Тогда AB=AC и ( small angle 1=angle 2 .) Что и требовалось доказать.
Видео:через точку А, лежащую вне окружности проведены две прямые. Одна прямая касается.. ФИПИСкачать

Теорема, обратная теореме о свойстве касательной
Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.
Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).
Видео:На окружности отмечены точки А и В так, что меньшая дуга АВ равна 68°. Прямая ВС касается окружностиСкачать

Построение касательной к окружности
Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).
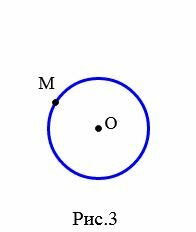 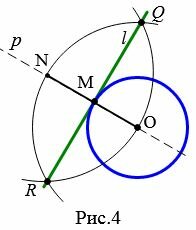 |
Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.
Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).
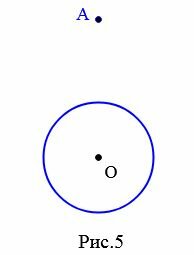 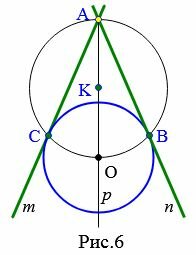 |
Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.
Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

Одна прямая касается окружности в точке к
Вопрос по геометрии:
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, BC=6. Найдите AK.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
🎥 Видео
ОГЭ по математике. На окружности отмечены точки (вар. 3) √ 17 модель геометрия ОГЭСкачать

Геометрия. ОГЭ по математике. Задание 16Скачать

ОКРУЖНОСТИ В ОГЭ ✨ #огэ #математика #егэ #геометрия #окружностьСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать

ЕГЭ задание 16Скачать

ОКРУЖНОСТИ В ОГЭ ✨ #огэ #математика #егэ #геометрия #окружностьСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Задание 16 ОГЭ по математике 2023Скачать

На окружности отмечены точки A и B так, что меньшая дуга AB равна 92 градуса. Прямая BC касается окрСкачать

16 задание ОГЭ по математике 2023 Касательная и секущая Shorts #shorts #огэпоматематике2023Скачать

ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

16 задание ОГЭ 2023 Окружность Касательная и секущая #ShortsСкачать

Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать

Самая сложная задача ОГЭСкачать