Окружность всегда можно описать около квадрат ромб треугольник прямоугольник

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Доказательство

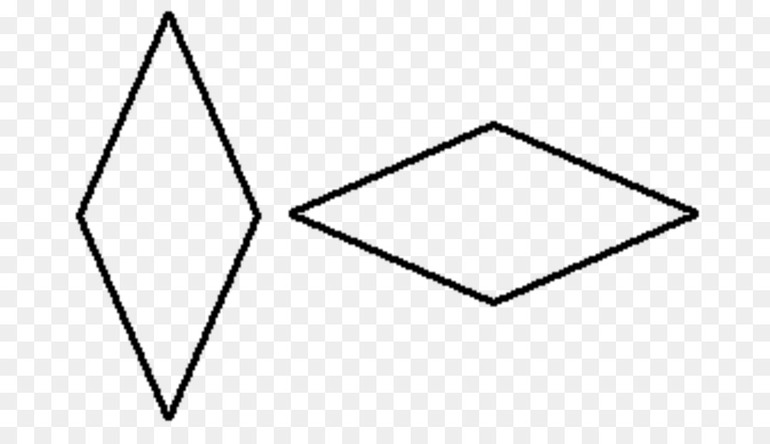
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:Геометрия 8. Урок 5 -Прямоугольник, ромб, квадрат - решение задач.Скачать

Окружность всегда можно описать около квадрат ромб

Видео:Геометрия Докажите, что если около ромба можно описать окружность, то этот ромб является квадратомСкачать

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:ЧЕТЫРЁХУГОЛЬНИК И ОКРУЖНОСТЬ: прямоугольник, квадрат, ромб, трапеция и окружностьСкачать

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac (a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Примеры вписанной окружности

• Треугольник
  
• Четырехугольник
  
• Многоугольник
  

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Нельзя описать окружность около ромба

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:№708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любойСкачать

Вокруг ромба нельзя описать окружность

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.

Примечание:

Окружность всегда можно описать:

Поделись с друзьями в социальных сетях:

Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать

Можно ли описать окружность около ромба, не являющегося квадратом?

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Ваш ответ

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

решение вопроса

Видео:Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,857
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Ромб — свойства, признаки и формулы нахождения параметров

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Общие сведения

Ромб является четырехугольником. В геометрии существует несколько видов последних. Для каждой фигуры предусмотрены свои соотношения, теоремы и формулы. Кроме того, математики выделяют специализированные алгоритмы, позволяющие точно и без ошибок определить тип фигуры.

Ученые разработали алгоритм для обучения, позволяющий за короткий промежуток времени перейти к решению сложных математических упражнений без каких-либо финансовых вложений. Он состоит из следующих элементов:

1. Сведения о ромбе: признаки, свойства и теоремы.
2. Формулы для нахождения некоторых параметров.

Изучение любой фигуры начинается всегда с ее определения, поскольку на основании этого возникают базовые знания.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Определение и частный случай

Ромбом называется параллелограмм с эквивалентными друг другу сторонами. О последнем можно сказать, что он относится к правильным четырехугольникам. Термин «правильный» означает равенство сторон одному значению. Следует отметить, что частным случаем ромба является квадрат, поскольку у него также имеются равные стороны. Эти фигуры имеют похожие свойства и формулы, однако некоторые соотношения отличаются.

Следовательно, необходимо правильно идентифицировать фигуру. Такая операция выполняется на основании признаков. Они присущи только конкретной фигуре и позволяют точно определить ее тип. Многие путают два ключевых понятия в геометрии: свойства и признаки. В учебниках существует множество определений, но, к сожалению, не все они понятны для новичков.

Признаками искомой фигуры называются характеристики, которые присущи только ей. Свойства — следствия из определений и доказательств теорем, используемые при доказательстве тождеств, утверждений и решения задач. Следует также обратить внимание на использование очередности. Первыми применяются признаки, а затем свойства.

Основные признаки

Признаки состоят из двух групп. Их формирование связано с количеством фигур, с которыми можно перепутать ромб. Определение последнего раскрывает их не полностью. Следовательно, математики для детального анализа разработали некоторый алгоритм, или первую группу. Различиями между искомой фигурой и параллелограммом являются следующие:

1. Эквивалентность всех сторон одной величине.
2. Углы, образованные пересечением диагоналей, являются прямыми.
3. Стороны, имеющие одну общую точку-вершину, равны между собой.
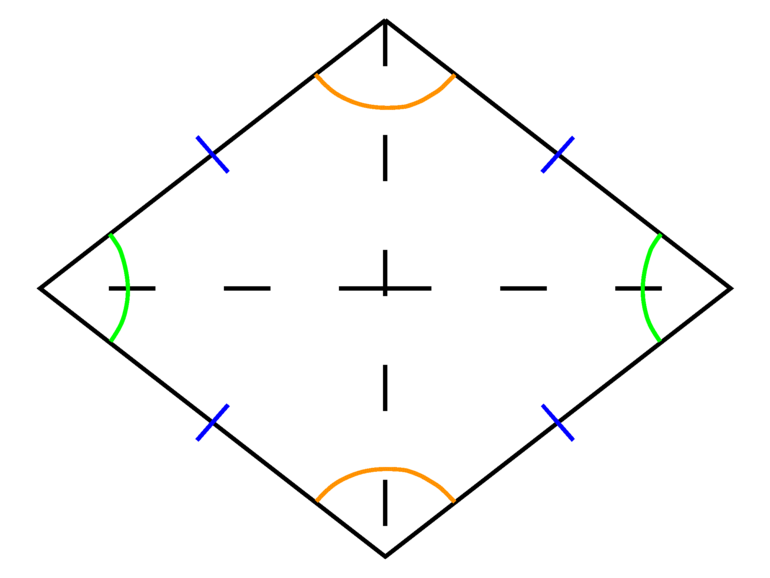
4. Биссектрисами внутренних углов ромба (делят угол на две половины) являются диагонали.
5. Диагонали пересекаются и образуют четыре равных прямоугольных треугольника и 2 группы равнобедренных треугольников, которые равны между собой.
6. Окружность можно вписать внутрь фигуры.
7. Высоты, образованные диагоналями при их пересечении, равны между собой.

Семь признаков отсеивают параллелограмм, но не дают провести разделение между ромбом и квадратом (прямоугольником), поскольку два последних также попадают под них. Для этого случая математики также разработали специальный алгоритм, который заключается в следующем:

1. Произвести идентификацию ромба по одному из признаков отличия от параллелограмма.
2. Внутренние углы не должны быть прямыми.
3. Вокруг ромба невозможно описать окружность.

Если у фигуры внутренние углы являются прямыми, то он является квадратом (прямоугольником). Кроме того, вокруг квадрата можно описать окружность. Алгоритмы идентификации являются очень простыми и надежными, поскольку вероятность ошибки эквивалентна нулевому значению. Существуют и другие методики определения типа фигуры, но они считаются сложными. Следовательно, на начальных стадиях обучения не рассматриваются.

Примером одной из них является операция интегрирования, основанная на вычислении размерностей (площадей) и объемов тел вращения, которые получаются в результате вращения ромба вокруг своей оси. Эти характеристики отличаются от характеристик параллелограмма и квадрата.

Свойства фигуры

Ромб является частным случаем параллелограмма и имеет все свойства, которые присущи этой фигуре. Новички не берут их во внимание, что приводит к увеличению объемов вычислений, а также возникновению ошибок. Свойствами параллелограмма являются следующие:

1. Сумма внутренних углов составляет 360 градусов.
2. Противолежащие углы эквивалентны одному значению (равны).
3. Противоположные стороны лежат на параллельных прямых и равны между собой.
4. Центром симметрии и описанной окружности является точка пересечения диагоналей. Через нее можно провести среднюю линию, которая делит стороны на два равных отрезка.
5. Треугольники, образованные диагоналями, эквивалентны.
6. Перпендикулярность биссектрис соседних углов.
7. Для равнобедренных треугольников, образованных пересечением диагоналей, последние являются биссектрисами, высотами и медианами.
8. Эквивалентность суммы квадратов диагоналей сумме квадратов всех сторон параллелограмма.
9. Точка пересечения диагоналей параллелограмма делит пополам.

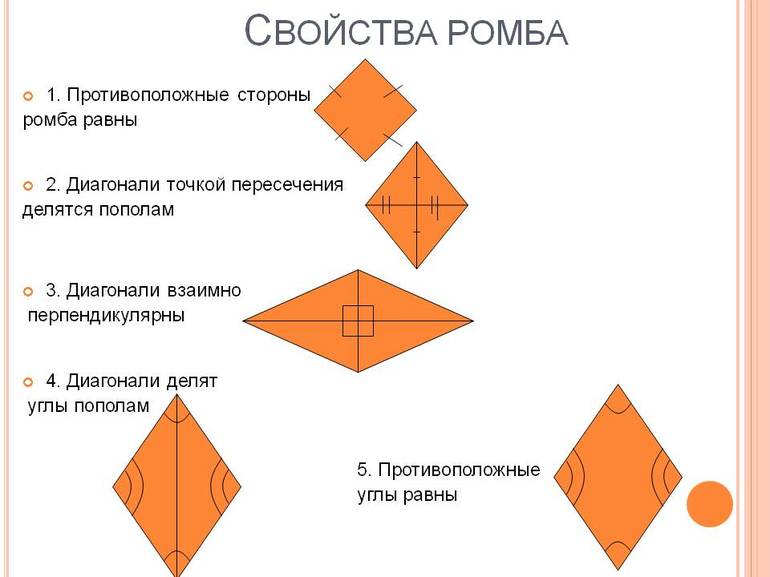
Следует отметить, что свойства ромба присущи только ему. К ним относятся следующие:

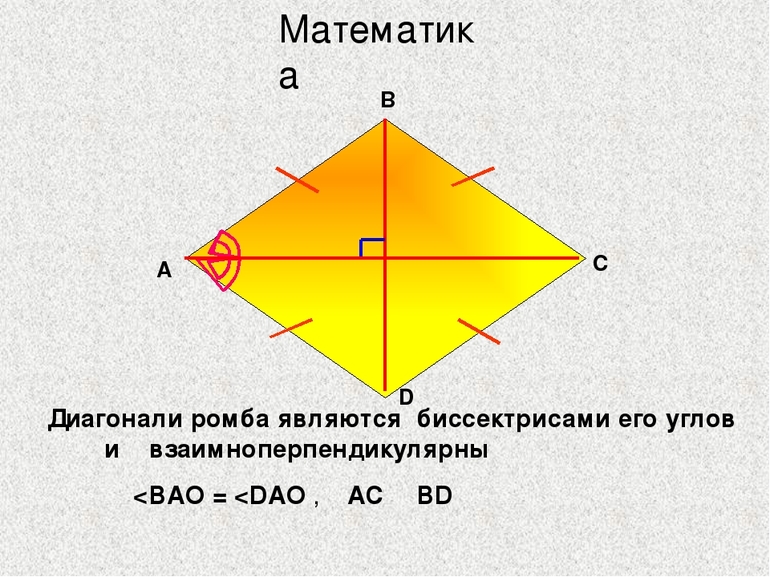
1. Диагонали пересекаются только под прямым углом и являются взаимоперпендикулярными. Кроме того, они являются биссектрисами его углов, и должны искомой точкой делиться пополам.
2. Сумма квадратов диагоналей m1 и m2 соответствует квадрату стороны, умноженной на 4.
3. Только в ромб можно вписать окружность, которая будет касаться точек-середин его сторон.
4. Пересечение диагоналей обозначается некоторой точкой, которая является центром вписанной окружности и симметрией фигуры.
5. Описать окружность можно только в том случае, когда диагонали ромба равны, то есть он является квадратом. Во всех остальных случаях этого сделать невозможно.

Все свойства были получены математиками при доказательствах различных теорем. Для некоторых также были использованы вспомогательные утверждения. Например, для второго применялась теорема Пифагора.

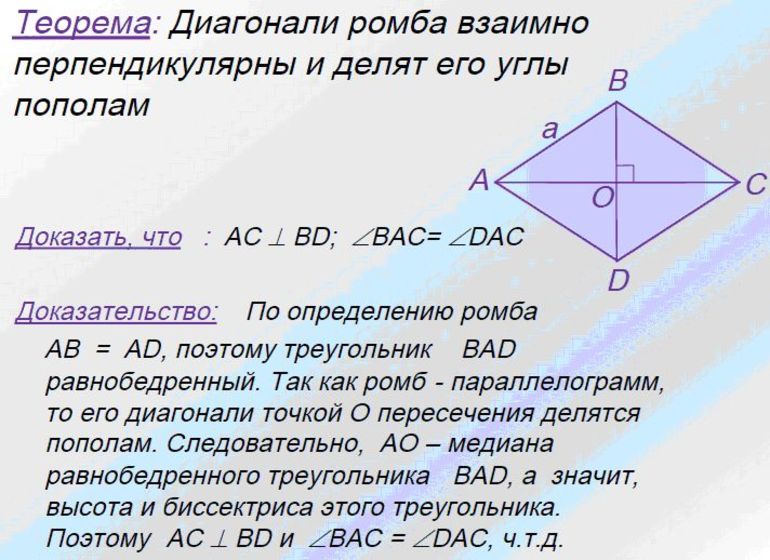
Теорема о свойствах диагоналей

Математики рекомендуют рассмотреть теорему о свойствах диагоналей ромба, которая гласит, что диагонали искомой фигуры пересекаются в одной точке и взаимоперпендикулярны, а также являются биссектрисами его углов. Для доказательства утверждения следует его разделить на две части: взаимоперпендикулярность диагоналей и последние являются биссектрисами углов фигуры.

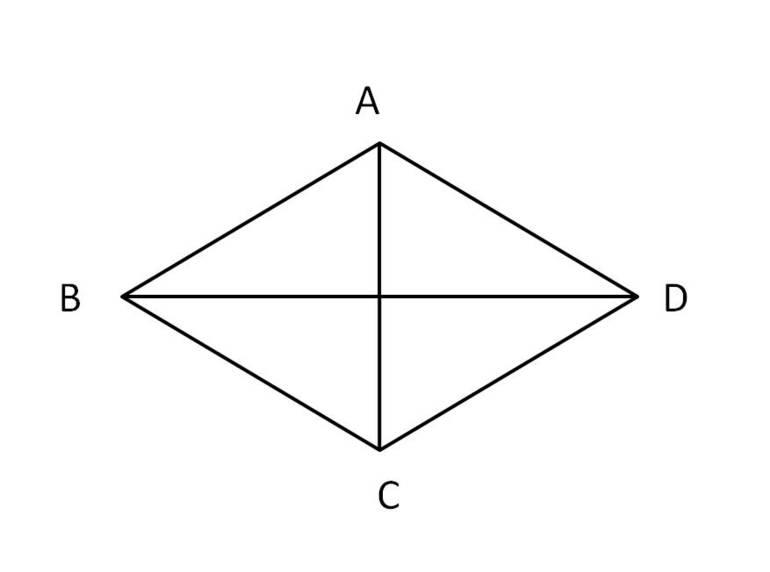
Необходимо начертить ромб ABCD со стороной «a», провести диагонали m1 (большую) и m2 (меньшую). Отметить их точку пересечения P. Существует много доказательств этого утверждения. Специалисты рекомендуют всегда выбирать самое простое, поскольку такой прием ценится на экзаменах. Одним из примеров рационального использования знаний является построение прямой в декартовой системе координат.

Согласно аксиоме геометрии, чтобы провести прямую, достаточно двух точек. Следовательно, нет смысла использовать 5, 10 и 20 элементов, поскольку все эти действия приведут к одному результату. Методика доказательства упрощенного типа считается самой эффективной. Следует рассмотреть треугольники ABC и ADC, полученные в результате проведения диагонали m1. Для удобства в геометрии слово «треугольник» заменяется символом «Δ», а угол — «∠». Они равны между собой по трем сторонам, то есть боковые стороны равны a (стороны ромба), а общая — эквивалентна значению диагонали m1.

Следует отметить, что они также являются равнобедренными, поскольку их боковые стороны равны между собой, то есть AB = BC = a и AD = CD = a. Далее следует обратить внимание на малую диагональ m1. Она опущена из вершины B и D на сторону AC. Исходя из свойства медианы в равнобедренном Δ, m1 является высотой и биссектрисой, то есть справедливо такое уравнение ∠ABC = ∠ADC = ∠ABP + ∠CPB = ∠APD + ∠CPD. Кроме того, высоты BP и DP образуют перпендикуляр со стороной AC.

Утверждение доказывается аналогично для ΔABC и ΔADC. Они равны по трем сторонам (AD = DC и AB = BC, а также по общей стороне BD) и являются равнобедренными, исходя из свойств сторон ромба. Диагональ m1 проходит через эти Δ. Она также является медианой, биссектрисой и высотой. Теорема доказана полностью.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Основные соотношения

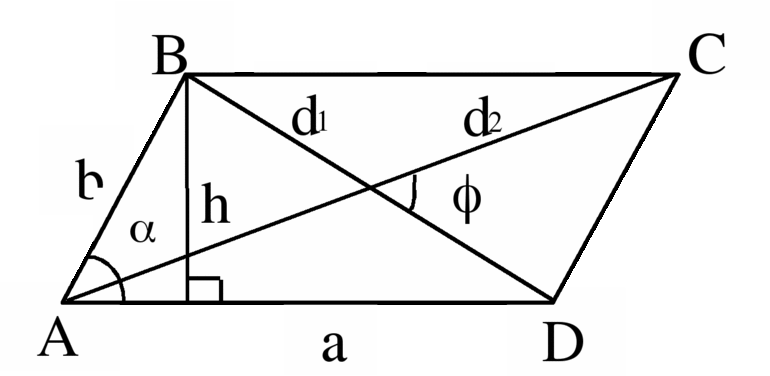
Для решения задач применяются формулы. Ромб не является исключением. Соотношения применяются для определения неизвестных параметров фигуры. Однако бывают случаи, когда недостаточно одной формулы, поскольку нужно связать несколько компонентов в единый процесс вычислений. Для корректного использования формул следует ввести класс некоторых обозначений:

1. Ромб обозначить набором латинских букв ABCD.
2. Стороны приравнять к некоторому числу, заданному в общей форме: AB = BC = CD = DA = a.
3. Диагонали: меньшая — m2 и большая = m1. Их точку пересечения следует обозначить литерой P.
4. Углы: ∠ABC = ∠ADC и ∠BAD = ∠BCD.
5. Характеристики вписанной окружности: диаметр D и радиус R.
6. Периметр и площадь (размерность): P и S соответственно.

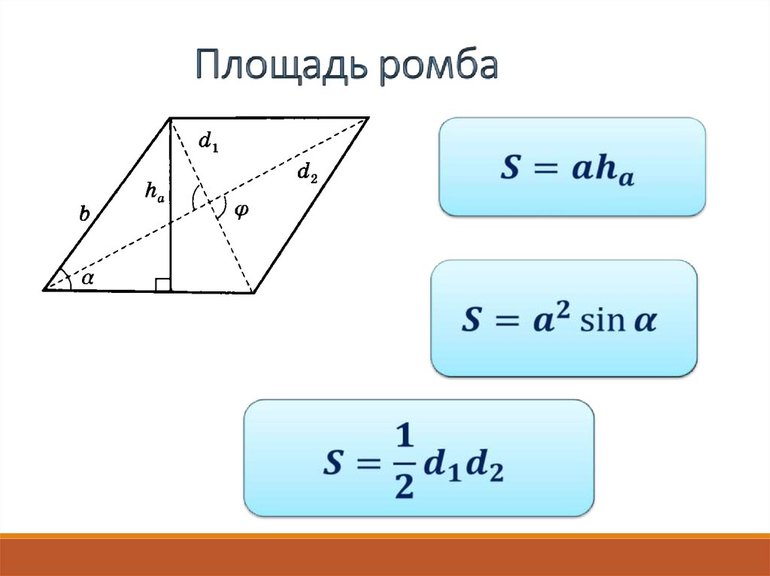
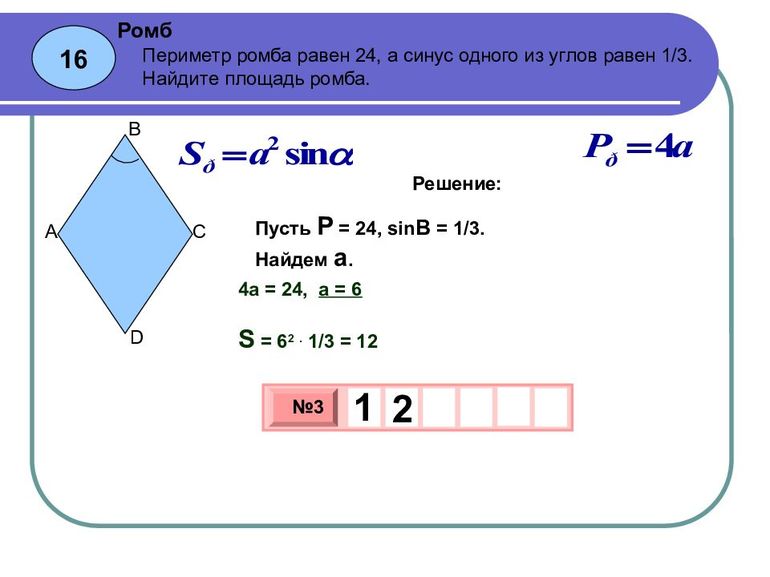
Периметр и площадь

Периметр ромба — характеристика, которая эквивалентна значению алгебраической суммы всех ее сторон. Площадью называется параметр геометрической фигуры, показывающий ее размерность в определенном геометрическом пространстве. Следует отметить, что величина S существует только у фигуры в двумерном пространстве. В трехмерном нужно рассматривать объем геометрического тела. Кроме того, у объемного тела есть параметр площади поперечного сечения. Эта величина является двумерной.

Периметр вычисляется по следующей формуле: P = 4 * a. Следует отметить, что величину a можно выражать через диагонали, площадь и другие характеристики. Базовая формула площади ромба имеет такой вид: S = a * BP = a * DP = a * AP = a * CP. Кроме того, размерность можно найти по следующим соотношениям:

1. S = a 2 * sin (∠ABC) = a 2 * sin (∠BCD) (через синус острого угла).
2. S = 2 * a * R.
3. S = (m1 * m2) / 2.
4. S = (4 * R 2 ) / sin (∠BAD).
5. S = [(m1)^2 * tg (∠BAD / 2)] / 2 = [(m2)^2 * tg (∠ABC / 2)] / 2.

В последней формуле при большем значении диагонали m1 следует брать тангенс острого угла, а при m2 — тангенс тупого угла. На это нужно обратить особое внимание, поскольку на этом моменте новички делают много ошибок, путая диагонали и углы.

Нахождение стороны

Длина стороны находится очень просто, поскольку математики выполнили доказательства некоторых тождеств. Они предлагают готовые решения в виде формул, позволяющих правильно выразить одну величину через другую, и подставить необходимые числовые значения:

1. a = S / BP = S / DP = S / AP = S / CP.
2. a = S^(½) / (sin (∠BAD))^(½).
3. a = S / 2 * R.
4. a = [(m1)^2 + (m2)^2]^(½) / 2.
5. a = P / 4.

Необходимо обратить внимание, что используются в некоторых соотношения тригонометрические функции. Последнее соотношение является формулой определения периметра. Если он известен, то легко вычислить значение стороны, используя обратную формулу P.

Другие соотношения

Осталось еще два параметра ромба — диагонали. Специалисты рекомендуют воспользоваться готовыми соотношениями для нахождения ее длины:

1. m1 = 2 * a * cos (∠BAD/2).
2. m2 = 2 * a * sin (∠BAD/2).

m1 = [4 * a 2 — (m2)^2]^(½) = [4 * S — (m2)^2]^(½).

m2 = [4 * a 2 — (m1)^2]^(½) = [4 * S — (m1)^2]^(½).

Следует также рассмотреть случай, когда окружность вписана в ромб. Такой прием применяется для расширения возможностей поиска неизвестной, что существенно позволит сэкономить время на расчетах. К формулам относятся следующие тождества:

1. R = S / 2 * a.
2. R = m1 * m2 / (2 * ((m1)^2 + (m2)^2)^(½)).
3. R = m1 * m2 / P = m1 * m2 / 4 * a.

Если нужно найти диаметр, то следует использовать такое соотношение: R = D / 2. Можно также выразить диагонали через стороны. Для этого следует подставить вместо m1 значение со стороной a.

Таким образом, математики предлагают специальный алгоритм, позволяющие без ошибок идентифицировать ромб, а затем применить соответствующие формулы для решения задачи.

Видео:Окружность Параллелограмм РомбСкачать

Можно ли описать окружность около ромба, не являющегося квадратом?

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Ваш ответ

Видео:ЧЕТЫРЕХУГОЛЬНИК и ОКРУЖНОСТЬ | ЕГЭ Математика | @matematikajСкачать

решение вопроса

Видео:Как узнать, что около четырехугольника можно описать окружность?😍 #математика #математикаегэ #егэСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,882
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:РОМБ . §5 геометрия 8 классСкачать

Вписанная окружность

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Примеры вписанной окружности

• Треугольник
  
• Четырехугольник
  
• Многоугольник
  

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.