- Ваш ответ
- решение вопроса
- Похожие вопросы
- Задача 29532 Две окружности радиусов 2 и 8 касаются.
- Условие
- Решение
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- 💥 Видео
Видео:Геометрия Окружность радиуса 4 касается внешним образом второй окружности в точке B. ОбщаяСкачать
Ваш ответ
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать
решение вопроса
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Похожие вопросы
- Все категории
- экономические 43,283
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,073
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Окружность. Как найти Радиус и ДиаметрСкачать
Задача 29532 Две окружности радиусов 2 и 8 касаются.
Условие
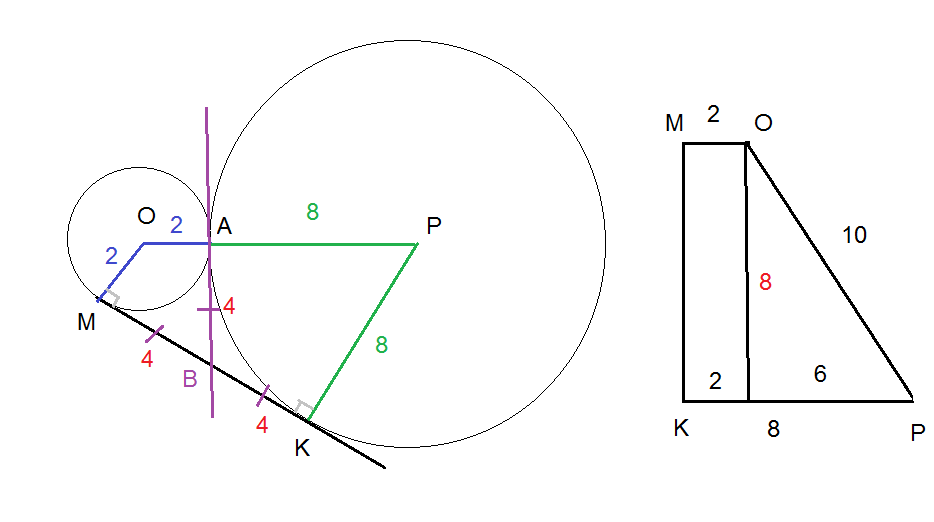
Две окружности радиусов 2 и 8 касаются друг друга внешним образом в точке А. Общая касательная к ним, проведенная через точку А , пересекает другую общую касательную в точке В . Найдите АВ. [9.34.]
Решение
Касательная перпендикулярна радиусу, проведённому в точку касания.
OM ⊥ MK
PK ⊥ MK
KOMP — прямоугольная трапеция.
MO=2
KP=8
OP=2+8=10
Проводим высоту из точки О на РК,
получаем прямоугольный треугольник с гипотенузой 10 и катетом
8-2=6
MK=8 ( по теореме Пифагора, египетский треугольник, 10 ; 8 ; 6)
По свойству касательных к окружности, проведенных из одной точки, отрезки касательных равны:
О т в е т. 4
Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать
Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Видео:✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, 💥 ВидеоГеометрия. ОГЭ по математике. Задание 16Скачать  Планиметрия 18 | mathus.ru| окружностей и их общей внутренней касательной касается третья окружностьСкачать  Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать  Решение планиметрических задач повышенного уровня сложностиСкачать  Планиметрия 15 | mathus.ru | Окружность, касающаяся двух других и их общей касательнойСкачать  Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать  ОГЭ Задание 26 Внешнее касание двух окружностейСкачать  Круг. Окружность (центр, радиус, диаметр)Скачать  Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Задача №16. Пересекающиеся и касающиеся окружности.Скачать  Параметр. Серия 13. Решение задач с окружностями. Касание двух окружностейСкачать  Окружность. Круг. 5 класс.Скачать  |
