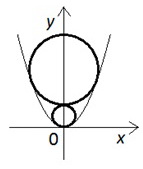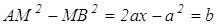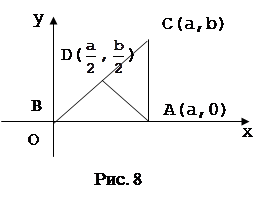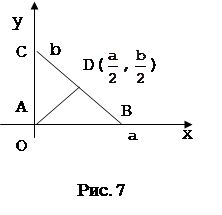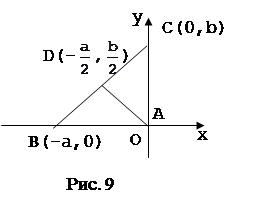Окружности w1, w2, w3, . помещены внутри параболы y = x 2 так, что w1 касается параболы в ее вершине и имеет радиус 0,5, окружность wт + 1 при каждом m касается окружности wm и ветвей параболы. Найти радиус окружности w2009.
Решение:
(№641 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)
Эту задачу можно решить, используя метод индукции.
Тогда уравнение окружности wт + 1 имеет вид:
Условие касания означает, что уравнение y + (y– (2Sn+ rn+1)) 2 = rn+1 2 имеет единственный корень, тогда его дискриминант:
Индукцией можно убедиться, что rn = n – 1/2.
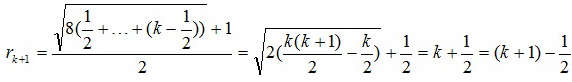
Значит, r2009 = 2009 – 1/2 = 2008,5.
- Взаимное расположение графиков квадратных трёхчленов
- Расположение графика квадратного трёхчлена относительно осей координат
- Точки пересечения двух парабол
- Примеры
- Как найти пересечение окружности и параболы
- Взаимное расположение графиков квадратных трёхчленов
- Расположение графика квадратного трёхчлена относительно осей координат
- Точки пересечения двух парабол
- Примеры
- Этап: построение окружности и параболы; нахождение точек их пересечения
- Как найти пересечение окружности и параболы
- 📸 Видео
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Взаимное расположение графиков квадратных трёхчленов
Расположение графика квадратного трёхчлена относительно осей координат
В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:
- ось симметрии $x = -frac$
- вершину параболы на оси симметрии $(–frac; -frac)$
- точку пересечения (0;c) с осью OY
Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c) .
Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.
Если $D gt 0$ , парабола имеет две точки пересечения с $x_1,2 = frac<-b pm sqrt>$ на оси OX.
Если D = 0 , парабола имеет одну точку пересечения $x_0 = -frac$, которая лежит на оси OX и является вершиной параболы.
Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.
Точки пересечения параболы с осью OX






Точки пересечения двух парабол
На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.
Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$
В точках пересечения выполняется равенство:
$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$
$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$
Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:
Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).
$ a_1 = a_2, b_1 = b_2, $
Две параболы совпадают
Бесконечное множество общих точек, $x in Bbb R$
$A = B = 0, C neq 0$
$ a_1 = a_2, b_1 = b_2, $
Параболы имеют вид
У них общая ось симметрии
$ x = -frac$, одна парабола находится над другой.
Ветки сходятся только на бесконечности.
Точек пересечения нет
$A = 0, B neq 0, C = 0$
$ a_1 = a_2, b_1 neq b_2 $
Параболы имеют вид
Обе проходят через точку (0;c).
Это – единственная точка пересечения.
Одна точка пересечения
$A = 0, B neq 0, C neq 0$
$ a_1 = a_2, b_1 neq b_2 $
Параболы имеют вид
Абсцисса точки пересечения
Одна точка пересечения (касание)
$A neq 0, B = 0, C = 0$
$ a_1 neq a_2, b_1 = b_2 $
Параболы имеют вид
Пересекаются при x=0 (точка касания)
Одна точка пересечения (касание) (0;c)
$A neq 0, B = 0, C neq 0$
$ a_1 neq a_2, b_1 = b_2 $
Параболы имеют вид
Не пересекаются, если
Две точки пересечения
Пересекаются в двух точках
Две точки пересечения
$A neq 0, B neq 0, C = 0$
$ a_1 neq a_2, b_1 neq b_2 $
Параболы имеют вид
$$ y = a_1 x^2+b_1 x+c $$
$$ y = a_2 x^2+b_2 x+c $$
Две точки пересечения
Две точки пересечения,
одна из которых (0;c)
$A neq 0, B neq 0, C neq 0$
$ a_1 neq a_2, b_1 neq b_2 $
Все параметры парабол разные
Две точки пересечения
Две точки пересечения
Одна точка пересечения (касание)
Одна точка пересечения
Точек пересечения нет
Точек пересечения нет
Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.
Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!
Примеры
Пример 1. Найдите точки пересечения параболы с осями координат:
Пересечение с осью OY: $<left< begin x = 0 \ y = -1end right.>$
Пересечение с осью OX:
$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$
$ Rightarrow left[ begin <left< begin x = frac \ y = 0 end right.> \ <left< begin x = -1 \ y = 0 end right.> end right.$ — две точки пересечения
Пересечение с осью OY: $<left< begin x = 0 \ y = 1end right.>$
Пересечение с осью OX:
$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$
$$ (4x-1)(x+1) = 0 Rightarrow$$
$ Rightarrow left[ begin <left< begin x = frac \ y = 0 end right.> \ <left< begin x = -1 \ y = 0 end right.> end right.$ — две точки пересечения
Пересечение с осью OY: $<left< begin x = 0 \ y = 1end right.>$
Пересечение с осью OX:
$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$
Парабола не пересекает ось OX
Пересечение с осью OY: $<left< begin x = 0 \ y = -4end right.>$
Пересечение с осью OX:
$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$
$$ Rightarrow (x-2)^2 = 0 Rightarrow <left< begin x = 2 \ y = 0 end right.>$$ — одна точка пересечения
Пример 2*. Даны две параболы
$$ y = 2x^2+5x+1 и y = x^2+3x+k $$
Найдите такое значение параметра k, чтобы параболы
1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.
$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$
$$ a_1 neq a_2, b_1 neq b_2 $$
A = 2-1 = 1, B = 5-3 = 2, C = 1-k
Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.
1) Параболы имеют две точки пересечения в двух случаях:
1 случай: $c_2 = c_1$, k = 1
2 случай: $c_2 ≠ c_1, D gt 0$
$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$
Оба случая можем объединить требованием $k gt 0$.
2) Параболы имеют одну точку пересечения, если:
$$ D = 4k = 0 Rightarrow k = 0 $$
3) Параболы не имеют общих точек, если:
$$ D = 4k lt 0 Rightarrow k lt 0 $$
Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$
Пример 3. Две параболы с общей вершиной
Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.
Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$
Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.
Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac-3x+1$.
$$ x_0 = — frac = — frac<2 cdot frac> = 3, D = b^2-4ac = 3^2-4 cdot frac cdot 1 = 7 $$
Уравнение искомой параболы: $y = ax^2+bx+c$
Пропорции для параметров (см. пример 3):
Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:
$$ <left< begin a = 1 \ b = -6a = -6 \ D = 14a = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ b^2-4ac = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ 36-4c = 14 end right.> Rightarrow <left< begin a = 1 \ b = -6 \ c = frac = 5,5 end right.>$$
$$ <left< begin a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end right.> Rightarrow <left< begin a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end right.> Rightarrow <left< begin a = -0,2 \ b = 1,2 \ c = — frac = -5,3 end right.> $$
$$ y = frac-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$
имеют общую вершину (3;-3,5)
Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac-2x+5$.
Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.
Координаты вершины траектории кометы:
$$ x_0 = -frac = -frac<2 cdot frac> = 3, D = b^2-4ac = 2^2-4 cdot frac cdot 5 = — frac $$
Уравнение траектории космического аппарата: $y = ax^2+bx+c$.
Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.
Пропорции для параметров (см. пример 3) с учетом c = 0:
Уравнение траектории космического аппарата с «перехватом» кометы в вершине:
Видео:ВСЁ ПРО ГРАФИКИ ЕГЭ 2024 (Прямая, Парабола, Окружность, Модуль, Гипербола, Корень, Области, Сдвиги)Скачать

Как найти пересечение окружности и параболы
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Взаимное расположение графиков квадратных трёхчленов
Расположение графика квадратного трёхчлена относительно осей координат
В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:
- ось симметрии $x = -frac $
- вершину параболы на оси симметрии $(–frac ; -frac )$
- точку пересечения (0;c) с осью OY
Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c) .
Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.
Если $D gt 0$ , парабола имеет две точки пересечения с $x_1,2 = frac > $ на оси OX.
Если D = 0 , парабола имеет одну точку пересечения $x_0 = -frac $, которая лежит на оси OX и является вершиной параболы.
Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.
Точки пересечения параболы с осью OX






Точки пересечения двух парабол
На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.
Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$
В точках пересечения выполняется равенство:
$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$
$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$
Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:
Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).
$ a_1 = a_2, b_1 = b_2, $
Две параболы совпадают
Бесконечное множество общих точек, $x in Bbb R$
$A = B = 0, C neq 0$
$ a_1 = a_2, b_1 = b_2, $
Параболы имеют вид
У них общая ось симметрии
$ x = -frac $, одна парабола находится над другой.
Ветки сходятся только на бесконечности.
Точек пересечения нет
$A = 0, B neq 0, C = 0$
$ a_1 = a_2, b_1 neq b_2 $
Параболы имеют вид
Обе проходят через точку (0;c).
Это – единственная точка пересечения.
Одна точка пересечения
$A = 0, B neq 0, C neq 0$
$ a_1 = a_2, b_1 neq b_2 $
Параболы имеют вид
Абсцисса точки пересечения
Одна точка пересечения (касание)
$A neq 0, B = 0, C = 0$
$ a_1 neq a_2, b_1 = b_2 $
Параболы имеют вид
Пересекаются при x=0 (точка касания)
Одна точка пересечения (касание) (0;c)
$A neq 0, B = 0, C neq 0$
$ a_1 neq a_2, b_1 = b_2 $
Параболы имеют вид
Не пересекаются, если
Две точки пересечения
Пересекаются в двух точках
Две точки пересечения
$A neq 0, B neq 0, C = 0$
$ a_1 neq a_2, b_1 neq b_2 $
Параболы имеют вид
$$ y = a_1 x^2+b_1 x+c $$
$$ y = a_2 x^2+b_2 x+c $$
Две точки пересечения
Две точки пересечения,
одна из которых (0;c)
$A neq 0, B neq 0, C neq 0$
$ a_1 neq a_2, b_1 neq b_2 $
Все параметры парабол разные
Две точки пересечения
Две точки пересечения
Одна точка пересечения (касание)
Одна точка пересечения
Точек пересечения нет
Точек пересечения нет
Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.
Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!
Примеры
Пример 1. Найдите точки пересечения параболы с осями координат:
Пересечение с осью OY: $ x = 0 \ y = -1end right.>$
Пересечение с осью OX:
$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$
Пересечение с осью OY: $ x = 0 \ y = 1end right.>$
Пересечение с осью OX:
$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$
$$ (4x-1)(x+1) = 0 Rightarrow$$
Пересечение с осью OY: $ x = 0 \ y = 1end right.>$
Пересечение с осью OX:
$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$
Парабола не пересекает ось OX
Пересечение с осью OY: $ x = 0 \ y = -4end right.>$
Пересечение с осью OX:
$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$
$$ Rightarrow (x-2)^2 = 0 Rightarrow x = 2 \ y = 0 end right.>$$ — одна точка пересечения
Пример 2*. Даны две параболы
$$ y = 2x^2+5x+1 и y = x^2+3x+k $$
Найдите такое значение параметра k, чтобы параболы
1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.
$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$
$$ a_1 neq a_2, b_1 neq b_2 $$
A = 2-1 = 1, B = 5-3 = 2, C = 1-k
Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.
1) Параболы имеют две точки пересечения в двух случаях:
1 случай: $c_2 = c_1$, k = 1
2 случай: $c_2 ≠ c_1, D gt 0$
$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$
Оба случая можем объединить требованием $k gt 0$.
2) Параболы имеют одну точку пересечения, если:
$$ D = 4k = 0 Rightarrow k = 0 $$
3) Параболы не имеют общих точек, если:
$$ D = 4k lt 0 Rightarrow k lt 0 $$
Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$
Пример 3. Две параболы с общей вершиной
Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.
Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$
Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.
Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac -3x+1$.
$$ x_0 = — frac = — frac > = 3, D = b^2-4ac = 3^2-4 cdot frac cdot 1 = 7 $$
Уравнение искомой параболы: $y = ax^2+bx+c$
Пропорции для параметров (см. пример 3):
Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:
$$ y = frac -3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$
имеют общую вершину (3;-3,5)
Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac -2x+5$.
Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.
Координаты вершины траектории кометы:
$$ x_0 = -frac = -frac > = 3, D = b^2-4ac = 2^2-4 cdot frac cdot 5 = — frac $$
Уравнение траектории космического аппарата: $y = ax^2+bx+c$.
Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.
Пропорции для параметров (см. пример 3) с учетом c = 0:
Уравнение траектории космического аппарата с «перехватом» кометы в вершине:
Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Этап: построение окружности и параболы; нахождение точек их пересечения
2 этап: построение окружности и параболы; нахождение точек их пересечения.
3 этап: количество точек пересечения окружности и параболы является ответом на поставленный вопрос.
№2. Найдите множество точек, для каждой из которых расстояния от двух данных точек равны.
Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А Предположим далее, что АВ=а, тогда в выбранной системе координат А(0,0) и В(а,0). Точка М(х,у) принадлежит искомому множеству тогда и только тогда, когда АМ=МВ, или, что то же самое, АМ 2= МВ 2 . Используя формулу расстояния от одной точки координатной плоскости до другой, получаем АМ 2 =x 2 +y 2 , MB 2 =(x-a) 2 +y 2 . Тогда х 2 +у 2 =(х-а) 2 + у 2
Равенство х 2 +у 2 =(х-а) 2 +у 2 и является алгебраической моделью ситуации, данной в задаче. На этом заканчивается первый этап ее решения (перевод задачи на координатный язык).
На втором этапе осуществляется преобразование полученного выражения, в результате которого получаем соотношение 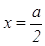
На третьем этапе осуществляется перевод языка уравнения на геометрический язык. Полученное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние 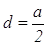
2.2 Задачи, обучающие координатному методу
Для разработки методики формирования умения применять координатный метод важно выявить требования, которые предъявляет логическая структура решения задач мышлению решающего. Координатный метод предусматривает наличие у обучающихся умений и навыков, способствующих применению данного метода на практике. Проанализируем решение нескольких задач. В процессе этого анализа выделим умения, являющиеся компонентами умения использовать координатный метод при решении задач. Знание компонентов этого умения позволит осуществить его поэлементное формирование.
Задача №1 . В треугольнике ABC: AC=b, AB=c, ВС=а, BD — медиана. Докажите, что 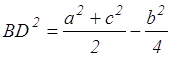
Выберем систему координат так, чтобы точка А служила началом координат, а осью Ох — прямая АС (рис. 2).
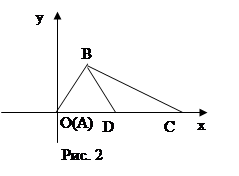
В выбранной системе координат точки А, С и D имеют следующие координаты: А(0,0), D(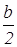
(умение вычислять координаты заданных точек). Обозначим координаты точки В через х и у. Тогда используя формулу для нахождения расстояний между двумя точками, заданными своими координатами, получаем:
х 2 +у 2 =с 2 , (x-b) 2 +y 2 =a 2 (1)
(умение находить расстояние между двумя точками, заданными координатами)
По той же формуле 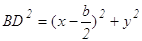
Используя формулы (1) находим х и у.
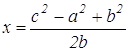
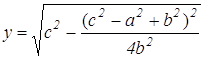
Далее, подставляя х и у в формулу (2), находим 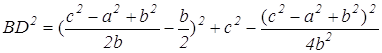
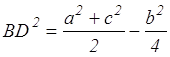
(умение выполнять преобразования алгебраических выражений)
Задача №2. Найти множество точек, для каждой из которых разность квадратов расстояний от двух данных точек есть величина постоянная.
Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А.
(умение оптимально выбирать систему координат).
Предположим АВ=а, тогда в выбранной системе координат А(0,0), В(а,0).
(умение находить координаты заданных точек)
Точка М(х,у) принадлежит искомому множеству тогда только тогда, когда AM 2 -MB 2 =b 2 где b — постоянная величина
(умение переводить геометрический язык на аналитический, составлять уравнения фигур).
Используя формулу расстояний между двумя точками, получаем:
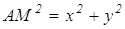
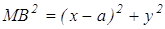
(умение вычислять расстояние между точками, заданными координатами), или 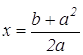
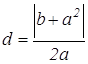
(умение видеть за уравнением конкретный геометрический образ)
Нетрудно видеть, что и для решения этой задачи необходимо овладение перечисленными выше умениями. Кроме того, для решения приведенной задачи, а также и других задач важно умение «видеть за уравнением» конкретный геометрический образ, которое является обратным к умению составлять уравнения конкретных фигур.
Выделенные умения являются основой при решении и более сложных задач.
Задача №3. В трапеции меньшая диагональ перпендикулярна основаниям. Найти большую диагональ, если сумма противоположных углов равна 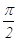
Направим оси координат по меньшей диагонали и одному из оснований (рис. 3).
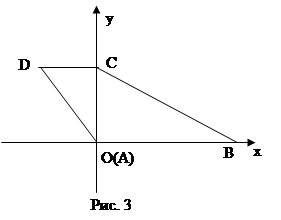
Тогда точка А имеет координаты (0,0), точка В — (а,0), точка С — (0,c), точка D — (b,c).
(умение находить координаты заданных точек)
Пусть 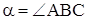
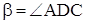
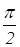
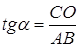
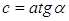
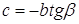
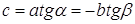
Из равенства (1) находим отношение 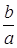
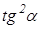
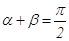
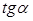
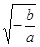
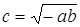
(умение выразить недостающие координаты через уже известные величины)
Далее воспользовавшись координатной формулой расстояния между двумя точками, найдем длину BD.
(умение вычислять расстояние между точками, заданными координатами)
Она равна 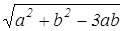
Итак, компонентами умения применять координатный метод в конкретных ситуациях являются следующие умения:
1. переводить геометрический язык на аналитический для одного типа задач и с аналитического на геометрический для другого;
2. стоить точку по заданным координатам;
3. находить координаты заданных точек;
4. вычислять расстояние между точками, заданными координатами;
5. оптимально выбирать систему координат;
6. составлять уравнения заданных фигур;
7. видеть за уравнением конкретный геометрический образ;
8. выполнять преобразование алгебраических соотношений.
Данные умения можно отработать на примере следующих задач, формирующих координатный метод:
1) задачи на построение точки по ее координатам;
2) задачи на нахождение координат заданных точек;
3) задачи на вычисление расстояния между точками, заданными координатами;
4) задачи на оптимальный выбор системы координат;
5) задачи на составление уравнения фигуры по ее характеристическому свойству;
6) задачи на определение фигуры по ее уравнению;
7) задачи на преобразование алгебраических равенств;
Приведем примеры таких задач.
I. Построение точек на плоскости.
С координатной прямой, а затем и с координатной плоскостью учащиеся знакомятся в 5-6 классах при изучении математического материала. При этом удобно использовать мультимедийные презентации, которые позволяют в динамике излагать необходимый материал, использовать всевозможные иллюстрации и звуковые эффекты, тем самым, заинтересовывая учащихся и являясь хорошим наглядным средством. Одним из примеров является презентация «Метод координат», опирающаяся на учебник [7]. (см. приложение 1). Приведем несколько примеров задач, которые можно использовать при изучении координатной плоскости. Эти задачи могут быть использованы:
— для оттачивания навыков построения точек по их координатам со всем классом;
— для дополнительных заданий отстающим ученикам;
— для развития интереса к изучаемой теме.
1) На координатной плоскости постройте точки А(7,2), B(-2,1), C(0,2).
2) Отметьте на плоскости несколько точек. Начертите произвольную систему координат и найдите в ней координаты заданных точек.
3) 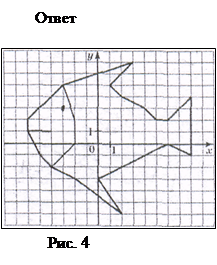
А) Камбала (Рис. 4)
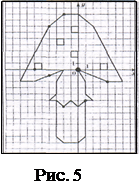
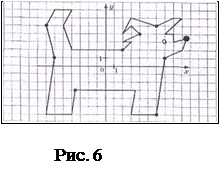
Б)Найдите координаты выделенных на рисунке точек, двигаясь по часовой стрелке от самой жирной точки. (Рис. 5 и 6)
II.Задачи на выбор системы координат
Выбор системы координат имеет очень важное значение при применении метода координат.
Для примера возьмем задачу, которая рассмотрена в учебнике [2] «Середина гипотенузы прямоугольного треугольника равноудалена от его вершин».
Первым шагом при применении метода координат является такой выбор осей и системы координат, при котором алгебраические выкладки становятся более простыми. Для данной задачи удачный выбор системы координат показан на рисунке 7. Таким образом, начало координат помещаем в точку А, а оси проводим через точки В и С так, чтобы эти точки лежали на положительных лучах осей. Следовательно, В(а,0) и С(0,b). Поэтому по формуле середины отрезка D(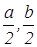
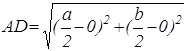
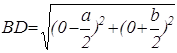
Поэтому AD=BD. А так как по определению середины отрезка BC=CD, то теорема доказана.
Можно выбрать систему координат и по-другому (рис.8, рис.9). Если выбрать оси совсем случайно, то легкую задачу можно превратить в очень трудную. Чтобы начать доказательство исходя из рисунка 10, нужно найти способ, позволяющий выразить алгебраически, что треугольник ABC имеет при вершине А прямой угол. Сделать это можно, но будет это не очень просто.
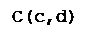 |
 |
Поэтому необходимо вырабатывать у учащихся, начиная с 6 класса, представления о возможности произвольного выбора системы координат. Эту работу целесообразно вести в процессе решения задач. В целях пропедевтической работы можно рекомендовать в 6 классе задачи из учебника на нахождение координат точек по рисунку, разнообразя их с помощью изменения направления осей и начала координат. (см. приложение1)
1. Длина отрезка АВ равна 5см. а)Выберите систему координат, в которой можно было бы наиболее просто определить координаты концов отрезка. б)Выберите систему координат так, чтобы координаты концов отрезка были бы: А (-2.5,0), В(2.5,0).
2. Постройте квадрат ABCD со стороной 2 см; отметьте точку М- центр квадрата. Поместите начало координат последовательно в точки A, B, C, D и выберите направление осей координат так, чтобы точка М в каждой системе координат имела координаты (1;1). За единичный примите отрезок длиной 1 см.
3. Треугольник ABC равносторонний (длина стороны равна 6 см.). Выберите систему координат так, чтобы можно проще было бы определить координаты его вершин.
III. Расстояние между точками
1) Точка М(а,с) находится от начала координат и точки А(4,0) соответственно на расстояниях 3 и 4 см. Определите координаты точки М.
2) Дан прямоугольник ABCD (АВ=2 см., ВС=4 см.). Как выбрать систему координат, чтобы его вершины имели координаты А(-1,-2), В(-1,2), С(1,2), D(l,-2)?
3) Длины сторон треугольника ABC равны 3, 4 и 5 см. Выберете систему координат и определите в ней координаты вершин треугольника ABC.
4) Вершины четырехугольника ABCD имеют следующие координаты: А(-3,1), В(3,6), С(2,2) и D(-4,3). Установите вид четырехугольника.
IV. Составление уравнения фигур
Это умение является одним из основных умений, которые необходимы при применении метода координат к решению задач.
1) Изобразите систему координат. Отметьте на оси Ох точки А и В. Запишите соотношения, которым удовлетворяют координаты точек, принадлежащих: а)отрезку АВ; б)лучу АВ; в)лучу ВА;
2) Запишите уравнение прямой, содержащей начало координат и точку А(2,5).
3) Запишите уравнение прямой, содержащей точки А(2,7)и В(1,3).
4) Изобразите на координатной плоскости произвольную прямую и найдите ее уравнение.
5) Запишите соотношения, которым удовлетворяю координаты точек прямоугольника с вершинами А(2,3), В(2,5), С(4,5), D(4,3).
6) Что представляют собой множества точек плоскости, координаты которых удовлетворяют неравенствам: а)х≤3; b)-5≤х≤0; c)x>1; d)x 2 +АР 2 не зависит от переменной b. Найдем АМ 2 и АР 2 используя формулу нахождения расстояния между двумя точками по их координатам: 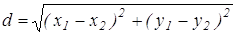
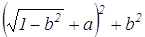
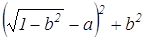
Пример 2. Доказать, что сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей. (Теорема Эйлера)
Решение: Введем прямоугольную систему координат как показано на рисунке 12.

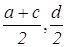
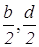
AD 2 =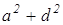
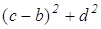
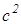
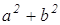
AC 2 =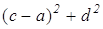
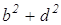
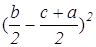
Запишем выражение, которое необходимо доказать, используя найденные нами значения.
AD 2 +BC 2 +DC 2 +AB 2 =AC 2 +BD 2 +4LP 2
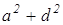
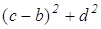
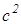
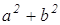
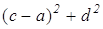
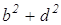
Раскроем скобки, приведем подобные и получим верное равенство 0=0. Значит, сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей.
Пример 3. Диаметры AB и CD окружности перпендикулярны. Хорда ЕА пересекает диаметр СD в точке К, хорда ЕС пересекает диаметр АВ в точке L. Докажите, что если СК:KD так же как 2:1, то AL:LB так же как 3:1.
Решение: Введем прямоугольную систему координат, направив оси по данным диаметрам AB и CD (рис. 13).
Радиус окружности будем считать равным 1. Тогда точки А, В, С, D будут иметь координаты (-1,0), (1,0), (0,-1), (0,1) соответственно. Так как СК:KD=2:1, то точка К имеет координаты (0,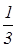
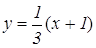
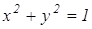
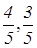
Найдем абсциссу точки L. Прямая СЕ задана уравнением 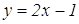
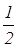
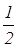
1. Доказать, что если в треугольнике две медианы конгруэнтны, то треугольник равнобедренный.
2. Найти множество таких точек Р, что отношение расстояний от каждой из них до двух данных точек равно а.
3. Докажите, что уравнение окружности с центром в точке С (а,с) и радиусом r имеет вид: (х-а) 2 +(у-с) 2 =r 2
4. Найти угол между прямыми Зх-4у+6=0 и 12х+5у+8=0
5. Определите расстояние от точки А(-3,4) до прямой у=х+2.
6. Вычислите площадь треугольника, вершины которого имеют следующие координаты: А (0,-2), В(6,2) и С(2,4) .
7. На прямой с даны три точки А, В, С так, что точка В лежит между точками А и С. В одной полуплоскости с границей а построены равносторонние треугольники АМВ и ВРС. Доказать, что середина отрезка РА, середина отрезка МС и точка В являются вершинами равностороннего треугольника.
8. Доказать, что для любой точки Р лежащей между вершинами В и треугольника ABC, справедливо равенство :
АВ 2 *РС+АС*ВР-АР 2 *ВС=ВС*ВР*РС.
9. Дан прямоугольник. Докажите, что сумма квадратов расстояний от произвольной точки, принадлежащей плоскости этого прямоугольника до его вершин, в два раза больше суммы квадратов расстояний от этой точки до сторон прямоугольника.
10. Доказать, что если через некоторую точку М провести прямую, пересекающую окружность в точках А и В, то произведение МА*МВ постоянно и не зависит от положения прямой.
11. Дан прямоугольник ABCD. Найти множество точек М, для которых MA 2 +MC 2 =MB 2 +MD 2 . (ответ: множество точек М есть плоскость)
Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Как найти пересечение окружности и параболы
Найдите все значения параметра а, при каждом из которых система имеет ровно 4 решения.
Первое уравнение задает части двух парабол (см. рисунок):
Второе уравнение задает окружность радиусом с центром
На рисунке видно, что четыре решения системы получаются в двух случаях.
1. Окружность касается каждой из ветвей обеих парабол.
2. Окружность пересекает каждую из ветвей обеих парабол в двух точках, лежащих по разные стороны от оси абсцисс.
Составим уравнение для ординат общих точек окружности и параболы Получим:
откуда
Чтобы окружность касалась парабол, уравнение должно иметь нулевой дискриминант: откуда
Во втором случае радиус окружности заключен между числами 3 и 9.
Ответ:
Аналоги к заданию № 484646: 484647 484648 511316 Все
📸 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Ищем точку пересечения парабол | Графики функций в ЕГЭСкачать
ЕГЭ задание 9 Координаты точки пересечения параболы и прямойСкачать
✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать

А вы знали эти свойства параболы?Скачать

ДВЕ ПАРАБОЛЫ / функции тип 9 / ЕГЭ #профиль #509253Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

М2052. Параболы, описанные вокруг окружностейСкачать

Уравнение окружности (1)Скачать

Как строить параболу? | TutorOnlineСкачать