Называется точка в которой встречаются все параллельные прямые (7 видео)

Параллельность прямых

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Содержание

Определение параллельности прямых
Свойства и признаки параллельных прямых
Задача 1
Задача 2
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Называется точка в которой встречаются все параллельные прямые
📸 Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Параллельные прямые. 6 класс.Скачать

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

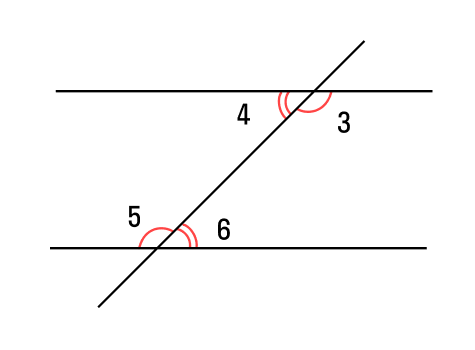
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

два внутренних накрест лежащих угла равны между собой:

два соответственных угла равны между собой:

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ

Относительно друг друга прямые могут быть параллельными, пересекающимися, скрещивающимися. Важно знать и уметь определять признаки взаимного положения двух прямых, изображенных на картине. Это даст возможность решать прямые (строить перспективу взаимного положения прямых) и обратные (определять их взаимное положение по изображению на картине) задачи.
Параллельные прямые. Наиболее часто встречаются параллельные прямые. Из практики наблюдательной перспективы известно, что параллельные прямые кажутся нам сходящимися в одной точке (железнодорожное полотно, шоссейная дорога, улица и т.д.). Для обоснования такого явления обратимся к проецирующему аппарату.
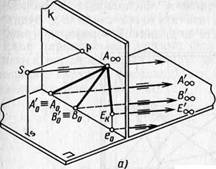
Зададим на проецирующем аппарате (рис. 38, а) пучок параллельных прямых , произвольно расположенных в предметной плоскости и ей параллельной . Построим перспективу каждой прямой. Для этого воспользуемся имеющимися точками Ао, Во, Ео, т. е. картинными следами этих прямых. Определим предельную точку каждой прямой (см. рис. 18). Заметим, что для всех заданных прямых она будет общая — Л «о, так как определяется одним и тем же лучом зрения SAoo, проведенным параллельно им до пересечения с линией горизонта.
Итак, произвольно направленные горизонтальные параллельные прямые на картине изображаются пучком прямых, сходящихся в одной предельной точке. Общая предельная точка произвольно расположенных горизонтальных параллельных прямых находится на линии горизонта и называется точкой схода. (Закон точки схода горизонтальных прямых.)
Заметим, что на картине (рис. 38, б) для параллельных прямых (А0А’оо, ВоВ’оо), лежащих в предметной плоскости и ей параллельной (ЕхЕ’оо), точка схода Л», может лежать в любом месте на линии горизонта в зависимости от их направления.

Рис. 38
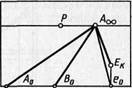
Если параллельные прямые глубинные, т. е. расположены перпендикулярно картинной плоскости, то точкой схода их будет главная эчка Р (рис. 39).
Итак, точкой схода глубинных параллельных прямых является главная точка картины. (Закон точки схода пучка глубинных прямых.)
Рассмотрим перспективу восходящих параллельных прямых общего положения (рис. 40). Если восходящие прямые параллельны, Го их проекции на предметную плоскость также между собой па-эаллельны. Проекции параллельных прямых лежат в предметной плоскости, поэтому будут иметь общую предельную точку а^ — точку Схода на линии горизонта. Тогда точка схода Лоо восходящих па-заллельных прямых будет лежать на перпендикуляре, проведенном линии горизонта через точку схода а» их проекций.
Итак, восходящие параллельные прямые общего положения имеют точку схода, расположенную над линией горизонта в произвольном месте и лежащую на одном перпендикуляре с точкой схода проекций этих прямых. (Закон точки схода пучка восходящих прямых общего положения.)
Аналогично строят изображения нисходящих параллельных прямых. Разница лишь в том, что их точка схода В^ будет расположена в произвольном месте под линией горизонта (рис. 41).

Рис 41
Итак, нисходящие параллельные прямые общего положения имеют точку схода, расположенную под линией горизонта в произвольном месте и лежащую на одном перпендикуляре с точкой схода их проекций. (Закон точки схода пучка нисходящих прямых общего положения.)
Таким образом, признаком параллельности прямых общего положения, изображенных на картине, является расположение на одном перпендикуляре точек схода прямых и их проекций. При этом точка схода проекций параллельных прямых должна лежать на линии горизонта.
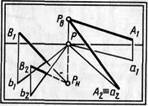
На рисунке 42 изображены две пары восходящих (Л,РВ и А2РВ) и нисходящих (ВРК и В2Рн) параллельных прямых особого положения. На основе общего правила их точки схода лежат на одном перпендикуляре к линии горизонта. Заметим, что в данном случае перпендикуляром является линия главного вертикала.
Итак, восходящие параллельные прямые особого положения имеют точку схода на линии главного вертикала над горизонтом, а их проекций — в главной точке. (Закон точки схода пучка восходящих прямых особого положения.)
Итак, нисходящие параллельные прямые особого положения имеют точку схода на линии главного вертикала под горизонтом, а их проекций — в главной точке картины. (Закон точки схода пучка нисходящих прямых особого положения.)

Рис. 42
Особые признаки имеют прямые частного положения, расположенные параллельно картине. Прямые, параллельные картине, изображаются на ней параллельными.
Если параллельные прямые фронтальные, то в перспективе они остаются параллельными между собой, а их проекции параллельны основанию картины, поскольку эти прямые и их проекции не имеют предельных точек (рис. 43).

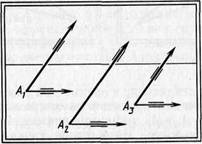
Рис. 43

Если параллельные прямые вертикальные, то в перспективе они остаются вертикальными и параллельными между собой, так как они не имеют предельной точки
Если параллельные прямые горизонтальные (параллельны картинной и предметной плоскостям), то в перспективе они и их проекции остаются параллельными между собой и основанию картины (рис. 45).
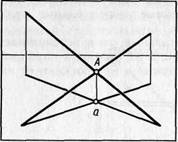
Пересекающиеся прямые. Зададим на картине две пересекающиеся в точке А прямые (рис. 46). Тогда проекции этих прямых на предметную плоскость пересекаются в точке а. Причем точка а — проекция точки пересечения А данных прямых. Точки А и а находятся на одном перпендикуляре. Если на картине точки пересечения двух прямых и их проекций лежат на одном перпендикуляре, то данные прямые пересекаются между собой в действительности.
Скрещивающиеся прямые. Зададим на картине две скрещивающиеся прямые (рис. 47). Если прямые скрещиваются, то они не могут быть параллельными и не должны иметь общей точки. Следовательно, на картине точки пересечения прямых и их проекций не должны лежать на одном перпендикуляре.

Рис. 46 Рис. 47

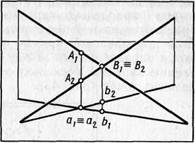
И действительно, если на картине перпендикуляр к предметной плоскости, проведенный из точки а1 пересечения проекций двух прямых, пересекает их в двух разных точках А1 и А2, то данные прямые скрещиваются между собой в действительности. На картине точка, кажущаяся пересечением двух прямых, является изображением двух различных точек В1 и В2, лежащих на скрещивающихся прямых. Обе точки расположены на одном луче зрения и поэтому на картине совпадают.
Заметим, что основания этих слившихся на картине точек различно удалены от основания картины (В1 ближе, В2 дальше). Это указывает на различное удаление от картины соответствующих им точек на заданных прямых (точка В, ближе к зрителю, а точка В2 дальше). Прямые скрещиваются в действительности, если на картине точка пересечения проекций данных прямых является проекцией двух различных точек.
Рассмотрим построение точек схода параллельных (горизонтальных, восходящих и нисходящих), а также пересекающихся и скрещивающихся прямых на примере перспективного изображения каркаса шалаша (рис. 48).

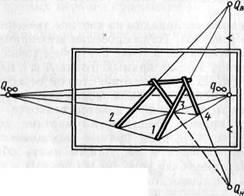
Рис. 48
Прямые, проведенные через концы жердей (У, 2, 3, 4) и конек шалаша, являются произвольно направленными горизонтальными параллельными. Они имеют общую точку схода Q,» на линии горизонта. Проекции наклонных жердей имеют точку схода q^ на линии горизонта. Наклонные жерди (/ и 2) будут восходящими параллельными прямыми, и их точка схода QB находится над линией горизонта и на перпендикуляре, проходящем через точку схода их проекций qx. Другая пара (3 и 4) наклонных жердей шалаша является нисходящими параллельными прямыми, и точка схода их QH находится на том же перпендикуляре под линией горизонта. Заметим, что все жерди шалаша имеют одинаковый наклон к земле, поэтому точки схода для восходящих и нисходящих прямых должны находиться на одном перпендикуляре к линии горизонта и на одинаковом расстоянии. По данному рисунку нетрудно определить, какие элементы шалаша параллельны, пересекаются и скрещиваются.

Вопросы и упражнения для самоконтроля
1. Какое положение точки в предметном пространстве называют общим, част
ным? Какие признаки на картине отражают это положение?
2. Как построить перспективу точки, заданной в предметном пространстве?
3. Задайте картину (100 ммX 70 мм) с ее элементами и 5 точек на ней: / — в пред
метной плоскости; 2 и 3 произвольно расположены в предметном пространстве, но
находятся ниже линии горизонта, при этом 2 ближе, чем 1, a 3 дальше, чем /; 4 и 5
находятся выше линии горизонта, при этом 4 на одинаковом удалении с 3, а 5 дальше
всех.
4. На картине (рис. 49) условно заданы 8 точек: вершины двух деревьев, две
сидящие на проводах птицы, две летящие птицы, лежащий на дороге предмет,
вершина телеграфного столба. Определите по изображению на картине, какая из
точек ближе и дальше, выше и ниже всех. Можно ли определить удаленность и
высоту двух летящих птиц? Дайте обоснование вашему суждению.

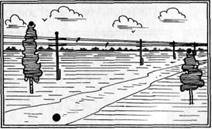
Рис. 49
5. Докажите, что перспектива прямой есть прямая.
6. Как построить перспективу отрезка?
7. Какое положение отрезка прямой называется общим, частным?
8. Как построить перспективу бесконечно продолженной прямой, лежащей в пред
метной плоскости или ей параллельной? Что называется предельной точкой прямой?
9. Что называется линией горизонта?

10. Что называется восходящей (нисходящей) прямой общего и особого по
ложения? Как их построить на картине? Укажите признаки, определяющие эти
прямые на картине.
11. На картине (рис. 50) заданы отрезки прямых. Определите их пространствен
ное положение. Укажите, где будут находиться их предельные точки. Назовите
отрезки прямых, изображенных на картине.
12. Какие частные положения может иметь прямая, расположенная в предмет
ном пространстве? Какие признаки на картине определяют их положение?
13. По изображению домика на картине (рис. 51) определите положение его

Рис. 50
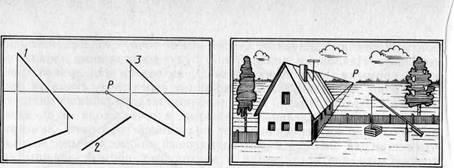
Рис. 51
элементов, отражающих горизонтальные, вертикальные, фронтальные, восходящие и нисходящие прямые.
14. Что называется следом прямой? Какие следы имеет прямая на картине?
Как построить на картине следы прямой?
15. Сколько и какие следы будут иметь прямые: восходящие и нисходящие об
щего и особого положения, горизонтальные, фронтальные, вертикальные? Задайте на
картине эти прямые и постройте их следы.
16. Что называется точкой схода прямых?
17. Где находится точка схода: глубинных прямых, восходящих и нисходящих
общего и особого положения, горизонтальных прямых, расположенных произ
вольно и под углом 45° к картинной плоскости?
18. При каком положении параллельные прямые не имеют точек схода и оста
ются параллельными? Дайте обоснование вашему суждению.

Видео:7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Называется точка в которой встречаются все параллельные прямые

§ 12. Параллельное проектирование и его свойства.

В начале учебника на плоскости изображены некоторые фигуры, расположенные в пространстве. Эти изображения строились с целью придать наглядность тому, о чём шла речь в соответствующей теореме или задаче.

Однако изображения пространственных фигур на плоскости строятся по определённым правилам и в школьном курсе геометрии обычно осуществляются с помощью метода параллельного проектирования, сущность которого состоит в следующем.

В пространстве выбирается произвольная плоскость π Плоскость проекций в начертательной геометрии чаще всего обозначают π . , которую называют плоскостью проекций или плоскостью изображения , и прямая l , пересекающая эту плоскость (рис. 71, а ).

Пусть M ′ — произвольная точка пространства. Через эту точку проведём прямую p , параллельную l . Точка M пересечения прямой p с плоскостью π называется параллельной проекцией точки M ′ на плоскость π в направлении прямой l . Если M ′ — точка плоскости π , то M совпадает с M ′ .

При этом часто пользуются обозначением: M = П ( M ′ ).

Прямую l и все прямые пространства, параллельные ей, называют проектирующими прямыми ; они определяют направление проектирования. Всякая плоскость пространства, параллельная проектирующей прямой, называется проектирующей плоскостью .

Фигура, которую проектируют или изображают, называется оригиналом. Для построения проекции фигуры достаточно построить проекции всех точек этой фигуры или проекции точек фигуры, её определяющих. На рисунке 71, б треугольник ABC является параллельной проекцией треугольника A ′ B ′ C ′ на плоскость π в направлении прямой l .

Замечание. Наряду с параллельным проектированием рассматривается также центральное проектирование фигур на плоскость. В этом случае проектирующие прямые проходят через одну точку — центр проектирования , произвольно выбранную вне плоскости проекций (рис. 71, в ).

Параллельное и центральное проектирование можно наблюдать в реальном пространстве: тень, которую отбрасывает предмет в солнечный день, является параллельной проекцией этого предмета, так как солнечные лучи можно считать приближённо параллельными вследствие большого удаления Солнца от Земли. А изображение на экране кинотеатра фигуры, заснятой на киноплёнку, является центральной проекцией этой фигуры.

На рисунках 72, 73, 74 изображены в параллельной проекции соответственно квадрат, треугольник и каркас тетраэдра. По этим рисункам можно сделать предположение, что ни величина угла, ни длина отрезка при параллельном проектировании, вообще говоря, не сохраняются.

Рассмотрим некоторые свойства параллельного проектирования.

1. Все точки проектирующей прямой проектируются в одну точку — точку пересечения этой прямой с плоскостью проекций (рис. 75).

В дальнейшем мы будем рассматривать проекции прямых, не параллельных проектирующим прямым.

2. Проекция прямой есть прямая. Действительно, все прямые, проектирующие точки данной прямой m ′ (рис. 76), принадлежат некоторой проектирующей плоскости, которая пересекает плоскость проекций по некоторой прямой m — параллельной проекции прямой m ′ .

Причём, так как через точку, не лежащую на данной прямой, можно провести лишь одну прямую, параллельную этой прямой (т. 6) (мы проводим прямые, параллельные прямой l ), то каждая точка прямой m ′ проектируется в единственную точку своей проекции — прямой m , и наоборот, каждая точка прямой m является проекцией единственной точки прямой m ′ .

Из доказательства этого свойства следует: три точки, лежащие на одной прямой, проектируются в три точки, также лежащие на одной прямой .

Также говорят, что три коллинеарные точки проектируются в три коллинеарные точки .

3. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Действительно, если прямые a ′ и b ′ лежат в одной проектирующей плоскости, то они проектируются в одну и ту же прямую, а именно, в прямую, по которой эта проектирующая плоскость пересекает плоскость проекций.

Пусть теперь прямые a ′ и b ′ параллельны (рис. 77) и не лежат в одной проектирующей плоскости.

Обозначим через α и β плоскости, образованные прямыми, проектирующими точки прямых соответственно a ′ и b ′ . Прямые a и b , по которым плоскости α и β пересекают плоскость проекции, не могут пересекаться, так как если бы эти прямые имели общую точку M , то и прямые a ′ и b ′ по свойству 2 имели бы общую точку M ′ , что невозможно в силу параллельности прямых a ′ и b ′ . А так как прямые a и b лежат в одной плоскости (плоскости проекций) и не имеют общей точки, то они параллельны, т. е. параллельными проекциями параллельных прямых, не лежащих в одной проектирующей плоскости, являются параллельные прямые.

Заметим, что плоскости α и β , проектирующие параллельные прямые a ′ и b ′ , не лежащие в одной проектирующей плоскости, параллельны (в п. 9.1 показано, что параллельные плоскости существуют; о свойствах параллельных плоскостей речь пойдёт в следующей главе).

4. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой. Отношение длин отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин проекций этих отрезков.

Если отрезки A ′ B ′ и B ′ C ′ лежат на одной прямой a ′ и проектируются на отрезки соответственно AB и BC прямой a (рис. 78), то по обобщённой теореме Фалеса в плоскости, определяемой прямыми a и a ′ , получаем A ′ B ′ : B ′ C ′ = AB : BC = m : n .

Пусть теперь отрезки A ′ B ′ и C ′ D ′ расположены соответственно на данных параллельных прямых a ′ и b ′ , не лежащих в одной проектирующей плоскости, и A ′ B ′ : C ′ D ′ = m : n ; AB и CD , a и b — соответственно их параллельные проекции на плоскость π (рис. 79).

Так как a ′ ‖ b ′ , то (по свойству 3) a ‖ b . Пусть E — такая точка прямой a , что четырёхугольник BCDE — параллелограмм. Тогда на прямой a ′ существует (единственная!) такая точка E ′ , что E ′ E ‖ DD ′ и A ′ B ′ : B ′ E ′ = AB : BE . А так как BC ‖ ED , то B ′ C ′ ‖ E ′ D ′ (по свойству 3), значит, B ′ C ′ D ′ E ′ — параллелограмм. Поэтому A ′ B ′ : C ′ D ′ = A ′ B ′ : B ′ E ′ = AB : BE = AB : CD , т. е. A ′ B ′ : C ′ D ′ = AB : CD = m : n .

Из этого свойства, очень важного для теории построений изображений пространственных фигур на плоскости, следует не менее важный вывод: если отрезок A ′ C ′ параллельно проектируется на отрезок AC и точка B ′ делит отрезок A ′ C ′ в отношении A ′ B ′ : B ′ C ′ = m : n , то точка B — проекция точки B ′ — делит отрезок AC в том же отношении m : n , т. е. AB : BC = A ′ B ′ : B ′ C ′ = m : n . В частности, середина отрезка A ′ C ′ параллельно проектируется в середину отрезка AC ( m : n = 1 : 1) (рис. 80).

Пусть M — внутренняя точка отрезка AB .

Определение. Число λ , равное отношению длин отрезков AM и MB , на которые точка M делит отрезок AB , называется простым отношением трёх точек A , B и M , лежащих на одной прямой, и обозначается ( AB ; M ), т. е. ( AB ; M ) = λ = AM : MB .

При этом точки A и B называются базисными , а точка M — делящей точкой.

Упорядоченность точек простого отношения необходима. Например, если AA 1 — медиана треугольника ABC , M — его центроид (точка пересечения медиан треугольника), то ( AA 1 ; M ) = AM : MA 1 = 2 : 1, но ( A 1 A ; M ) = A 1 M : MA = 1 : 2 (рис. 81). Поэтому, если AM ≠ MA 1 , то

( AA 1 ; M ) ≠ ( A 1 A ; M ).

Учитывая свойство 4 параллельного проектирования, можно сделать вывод: простое отношение трёх точек, лежащих на одной прямой, при параллельном проектировании сохраняется . В этом случае также говорят, что простое отношение трёх точек, лежащих на одной прямой, — инвариант параллельного проектирования .

Свойства фигуры, сохраняющиеся при параллельном проектировании, называются аффинными свойствами этой фигуры. Например, свойства прямых быть параллельными — аффинное свойство этих прямых; инвариантность простого отношения трёх точек одной прямой — аффинное свойство таких точек.

Подробнее о параллельном проектировании и изображениях фигур на плоскости читайте в конце учебника.

Определение. Проектирование в направлении прямой, перпендикулярной плоскости проекций, называется ортогональным.

Удобно пользоваться обозначением: M = П ( M ′ ).

Ортогональное проектирование является частным случаем параллельного и обладает всеми его свойствами. Однако, если при параллельном проектировании, не являющимся ортогональным, длина проекции отрезка может быть меньше, больше или равна длине самого отрезка, то при ортогональном проектировании длина проекции отрезка не больше, чем длина самого отрезка, и длины этих отрезков связаны соотношением: П ( AB ) = | AB |•cos ϕ , где ϕ — величина угла между прямой AB и плоскостью проекций α .

Задания для работы с интернет-ресурсами

1. Наберите в поисковой системе слова «Перпендикулярность прямой и плоскости», «Перпендикуляр и наклонная к плоскости», «Наклонная и её проекция на плоскость», «Теорема о трёх перпендикулярах». На изображениях куба, параллелепипеда найдите рёбра и диагонали, перпендикулярные граням и сечениям этих многогранников. Найдите видеоролики с лекциями опытных педагогов и геометров, в которых выражаются различные взгляды как на теорию, так и на решение задач по этим вопросам.

2. Наберите в поисковой системе слова «угол между наклонной и плоскостью». Поищите задачи ЕГЭ типа С-2, в которых используется нахождение угла между прямой и плоскостью, посмотрите, как они решаются, попробуйте решить их самостоятельно. Если вам удалось найти в Интернете тренинг по решению задач этой темы, то попытайтесь им воспользоваться. Однако решать такие задачи целесообразнее после изучения темы «Расстояния в пространстве». Скоро вы изучите эту тему.

3. Изображения фигур на плоскости и в живописи подчиняются определённым законам. Найдите в Интернете такие имена, как Филиппо Брунеллески (1377—1446), Леонардо да Винчи (1452—1519) и Альбрехт Дюрер (1471—1528). Вы увидите творчество этих великих художников. Однако существует направление, которое называется импоссибилизм (impossibility — невозможность) — изображение невозможных фигур, парадоксов. Представителем этого направления живописи является известный голландский художник Мауриц Эшер (1898—1972). Найдите статьи, посвящённые его творчеству, а главное, найдите сами репродукции картин, которые представляют большой интерес и с точки зрения геометрии.