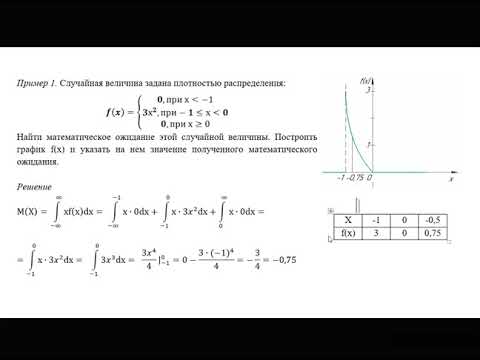
В этом разделе рассмотрены числовые характеристики только двумерных случайных величин, поскольку обобщение на случай 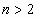
Пусть ( x , h ) — двумерная случайная величина, тогда M( x , h )=(M( x ), M( h )), т.е. математическое ожидание случайного вектора — это вектор из математических ожиданий компонент вектора.
Если ( x , h ) — дискретный случайный вектор с распределением
| y1 | y2 | . | ym | |
| x1 | p11 | p12 | . | p1m |
| x2 | p12 | p12 | . | p2m |
| . | . | . | pij | . |
| xn | pn1 | pn2 | . | pnm |
то математические ожидания компонент вычисляются по формулам:
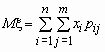
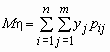
Эти формулы можно записать в сокращенном виде.
Обозначим 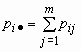
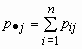
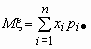
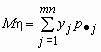
Если p( x , h )(x, y)- совместная плотность распределения непрерывной двумерной случайной величины ( x , h ), то
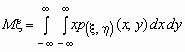
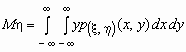
Поскольку 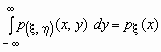
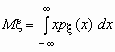
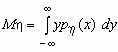
Понятие дисперсии обобщается на многомерные случайные величины нетривиальным образом. Это обобщение будет сделано в следующем разделе. Здесь лишь приведем формулы для вычисления дисперсии компонент двумерного случайного вектора.
Если ( x , h ) — двумерная случайная величина, то
D x = M( x — M x ) 2 = M x 2 — M( x ) 2 , D h = M( h — M h ) 2 = M h 2 — M( h ) 2 .
Входящие в эту формулу математические ожидания вычисляются по приведенным выше формулам.
Между случайными величинами может существовать функциональная зависимость. Например, если x — случайная величина и h = x 2 , то h — тоже случайная величина, связанная с x функциональной зависимостью. В то же время между случайными величинами может существовать зависимость другого рода, называемая стохастической. В разделе, посвященном условным распределениям уже обсуждалась такая зависимость. Из рассмотренных там примеров видно, что информация о значении одной случайной величины (одной компоненты случайного вектора) изменяет распределение другой случайной величины (другой компоненты случайного вектора), а это может, вообще говоря, изменить и числовые характеристики случайных величин.
Математическое ожидание, вычисленное по условному распределению, называется условным математическим ожиданием.
Для двумерного дискретного случайного вектора ( x , h ) с распределением
| y1 | y2 | . | ym | |
| x1 | p11 | p12 | . | p1m |
| x2 | p12 | p12 | . | p2m |
| . | . | . | pij | . |
| xn | pn1 | pn2 | . | pnm |
условное математическое ожидание случайной величины x при условии, что случайная величина h принимает значение yj, вычисляется по формуле 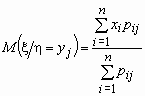
Аналогично, условное математическое ожидание случайной величины h при условии, что случайная величина x принимает значение xi, равно 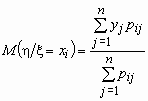
Видно, что условное математическое ожидание случайной величины x является функцией значений случайной величины h , т.е. M( x / h = y) = f1(y) и, совершенно аналогично, M( h / x = x) = f2(x).
Функцию f1(y) называют регрессией случайной величины x на случайную величину h , а f2(x) — регрессией случайной величины h на случайную величину x .
Если p( x , h )(x, y) совместная плотность вероятностей двумерной случайной величины ( x , h ), то
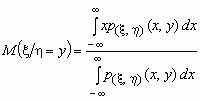
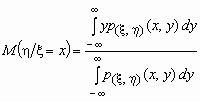
Если между случайными величинами x и h существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov( x , h ). Ковариацию вычисляют по формулам cov( x , h )=M[( x — M x )( h — M h )] = M( x h ) — M x M h .
Если случайные величины x и h независимы, то cov( x , h )=0.
Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.
cov( x , x ) = D x ;
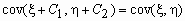
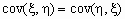
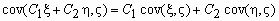
Ковариационной матрицей случайного вектора ( x , h ) называется матрица вида
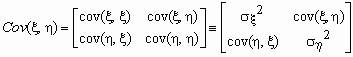
Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин ( x , h ).
Как уже отмечалось ранее, дисперсия суммы независимых случайных величин равна сумме их дисперсий: 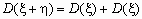
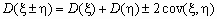
Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений. Для исключения этой зависимости вместо ковариации используется безразмерный коэффициент корреляции 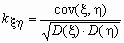
Этот коэффициент обладает следующими свойствами:
его модуль не превосходит единицы, т.е. 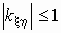
если x и h независимы, то k( x , h )=0 (обратное неверно!);
если 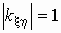
где a и b- некоторые числовые коэффициенты;
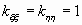
Корреляционной матрицей случайного вектора называется матрица
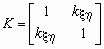
Если 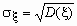
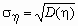
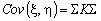
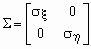
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать

Двумерная непрерывная случайная величина
Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю — двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.
Видео:Случайный вектор двумерной случайной величиныСкачать

Система непрерывных случайных величин: теория
Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(Xlt x, Ylt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:
Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:
Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:
$$P(x_1 le X le x_2, y_1 le Y le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$
Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:
Если для всех значений $(x,y)$ выполняется равенство
то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).
Видео:Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

Примеры решений
Задача 1. Дана плотность распределения вероятностей системы $$ f(x)= left< begin C, mbox O(0,0), A(4,0), B(4,1)\ 0, mbox \ end right. $$ Найти:
$C, rho_1(x), rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_, F(2,10), M[X|Y=1/2]$.
Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ — плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=csqrt, quad A(0;0), B(-1;-1), C(-1;0) $$
Задача 3. Интегральная функция распределения случайного вектора (X,Y): $$ F(x)= left< begin 0, mbox x le 0 mbox yle 0\ (1-e^)(1-e^), mbox x gt 0 mbox ygt 0\ end right. $$ Найти центр рассеивания случайного вектора.
Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У) $$f(x,y)=C e^$$ Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.
Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 sin(x+y)$ в квадрате $0 le x le pi/2$, $0 le y le pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).
Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 le x le pi/2$, $0 le y le pi/2$, если функция распределения системы $F(x,y)=sin x sin y$.
Задача 7. Плотность вероятности системы случайных величин равна $$f(x,y) = c(R-sqrt), quad x^2+y^2 lt R^2.$$ Определить:
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $alt R$, если центры обоих кругов совпадают с началом координат.
Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y $$f(x,y)=frac.$$ Найти величину $с$; определить законы распределения $F_1(x)$, $F_2(y)$, $f_1(x)$, $f_2(y)$, $f(x/y)$; построить графики $F_1(x)$, $F_2(y)$; вычислить моменты $m_x$, $m_y$, $D_x$, $D_y$, $K_$.
Видео:Корреляция и ковариация двумерной случайной величиныСкачать

Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Видео:Математическое ожидание-3 типа задачСкачать

Системы случайных величин
Назначение сервиса . С помощью сервиса по заданному закону распределения можно найти:
- ряды распределения X и Y, математическое ожидание M[X], M[Y], дисперсию D[X], D[Y];
- ковариацию cov(x,y), коэффициент корреляции rx,y, условный ряд распределения X, условное математическое ожидание M[X/Y=yi];
Кроме этого, дается ответ на вопрос, «зависимы ли случайные величины X и Y ?».
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Пример №1 . Двумерная дискретная случайная величина имеет таблицу распределения:
| Y/X | 1 | 2 | 3 | 4 |
| 10 | 0 | 0,11 | 0,12 | 0,03 |
| 20 | 0 | 0,13 | 0,09 | 0,02 |
| 30 | 0,02 | 0,11 | 0,08 | 0,01 |
| 40 | 0,03 | 0,11 | 0,05 | q |
Найти величину q и коэффициент корреляции этой случайной величины.
Решение. Величину q найдем из условия Σpij = 1
Σpij = 0,02 + 0,03 + 0,11 + … + 0,03 + 0,02 + 0,01 + q = 1
0.91+q = 1. Откуда q = 0.09
Находим ряды распределения X и Y.
Пользуясь формулой ∑P(xi,yj) = pi (j=1..n), находим ряд распределения X.
| X | 10 | 20 | 30 | 40 | |
| P | 0.26 | 0.24 | 0.22 | 0.28 | ∑Pi = 1 |
Математическое ожидание M[X] = 10*0.26 + 20*0.24 + 30*0.22 + 40*0.28 = 25.2
Дисперсия D[X] = 10 2 *0.26 + 20 2 *0.24 + 30 2 *0.22 + 40 2 *0.28 — 25.2 2 = 132.96
Среднее квадратическое отклонение σ(x) = sqrt(D[X]) = sqrt(132.96) = 11.531
Пользуясь формулой ∑P(xi,yj) = qj (i=1..m), находим ряд распределения Y.
| Y | 1 | 2 | 3 | 4 | |
| P | 0.05 | 0.46 | 0.34 | 0.15 | ∑Pi = 1 |
Математическое ожидание M[Y].
M[y] = 1*0.05 + 2*0.46 + 3*0.34 + 4*0.15 = 2.59
Дисперсия D[Y] = 1 2 *0.05 + 2 2 *0.46 + 3 2 *0.34 + 4 2 *0.15 — 2.59 2 = 0.64
Среднее квадратическое отклонение σ(y) = sqrt(D[Y]) = sqrt(0.64) = 0.801
Ковариация cov(X,Y) = M[X·Y] — M[X]·M[Y] = 2·10·0.11 + 3·10·0.12 + 4·10·0.03 + 2·20·0.13 + 3·20·0.09 + 4·20·0.02 + 1·30·0.02 + 2·30·0.11 + 3·30·0.08 + 4·30·0.01 + 1·40·0.03 + 2·40·0.11 + 3·40·0.05 + 4·40·0.09 — 25.2 · 2.59 = -0.068
Коэффициент корреляции rxy = cov(x,y)/σ(x)&sigma(y) = -0.068/(11.531*0.801) = -0.00736
Пример 2 . Данные статистической обработки сведений относительно двух показателей X и Y отражены в корреляционной таблице. Требуется:
- написать ряды распределения для X и Y и вычислить для них выборочные средние и выборочные средние квадратические отклонения;
- написать условные ряды распределения Y/x и вычислить условные средние Y/x;
- изобразить графически зависимость условных средних Y/x от значений X;
- рассчитать выборочный коэффициент корреляции Y на X;
- написать выборочное уравнение прямой регрессии;
- изобразить геометрически данные корреляционной таблицы и построить прямую регрессии.
Решение. Упорядоченная пара (X,Y) случайных величин X и Y называется двумерной случайной величиной, или случайным вектором двумерного пространства. Двумерная случайная величина (X,Y) называется также системой случайных величина X и Y.
Множество всех возможных значений дискретной случайной величины с их вероятностями называется законом распределения этой случайной величины.
Дискретная двумерная случайная величина (X,Y) считается заданной, если известен ее закон распределения:
P(X=xi, Y=yj) = pij, i=1,2. n, j=1,2. m
| X / Y | 20 | 30 | 40 | 50 | 60 |
| 11 | 2 | 0 | 0 | 0 | 0 |
| 16 | 4 | 6 | 0 | 0 | 0 |
| 21 | 0 | 3 | 6 | 2 | 0 |
| 26 | 0 | 0 | 45 | 8 | 4 |
| 31 | 0 | 0 | 4 | 6 | 7 |
| 36 | 0 | 0 | 0 | 0 | 3 |
События (X=xi, Y=yj) образуют полную группу событий, поэтому сумма всех вероятностей pij(i=1,2. n, j=1,2. m), указанных в таблице, равна 1.
1. Зависимость случайных величин X и Y.
Находим ряды распределения X и Y.
Пользуясь формулой ∑P(xi,yj) = pi (j=1..n), находим ряд распределения X.
| X | 11 | 16 | 21 | 26 | 31 | 36 | |
| P | 2 | 10 | 11 | 57 | 17 | 3 | ∑Pi = 100 |
Математическое ожидание M[X].
M[x] = (11*2 + 16*10 + 21*11 + 26*57 + 31*17 + 36*3 )/100 = 25.3
Дисперсия D[X].
D[X] = (11 2 *2 + 16 2 *10 + 21 2 *11 + 26 2 *57 + 31 2 *17 + 36 2 *3 )/100 — 25.3 2 = 24.01
Среднее квадратическое отклонение σ(x).
Пользуясь формулой ∑P(xi,yj) = qj (i=1..m), находим ряд распределения Y.
| Y | 20 | 30 | 40 | 50 | 60 | |
| P | 6 | 9 | 55 | 16 | 14 | ∑Pi = 100 |
Математическое ожидание M[Y].
M[y] = (20*6 + 30*9 + 40*55 + 50*16 + 60*14 )/100 = 42.3
Дисперсия D[Y].
D[Y] = (20 2 *6 + 30 2 *9 + 40 2 *55 + 50 2 *16 + 60 2 *14 )/100 — 42.3 2 = 99.71
Среднее квадратическое отклонение σ(y).
Поскольку, P(X=11,Y=20) = 2≠2·6, то случайные величины X и Y зависимы.
2. Условный закон распределения X.
Условный закон распределения X(Y=20).
P(X=11/Y=20) = 2/6 = 0.33
P(X=16/Y=20) = 4/6 = 0.67
P(X=21/Y=20) = 0/6 = 0
P(X=26/Y=20) = 0/6 = 0
P(X=31/Y=20) = 0/6 = 0
P(X=36/Y=20) = 0/6 = 0
Условное математическое ожидание M[X/Y=20).
M[X/Y=y] = 11*0.33 + 16*0.67 + 21*0 + 26*0 + 31*0 + 36*0 = 14.33
Условная дисперсия D[X/Y=20).
D[X/Y=y] = 11 2 *0.33 + 16 2 *0.67 + 21 2 *0 + 26 2 *0 + 31 2 *0 + 36 2 *0 — 14.33 2 = 5.56
Условный закон распределения X(Y=30).
P(X=11/Y=30) = 0/9 = 0
P(X=16/Y=30) = 6/9 = 0.67
P(X=21/Y=30) = 3/9 = 0.33
P(X=26/Y=30) = 0/9 = 0
P(X=31/Y=30) = 0/9 = 0
P(X=36/Y=30) = 0/9 = 0
Условное математическое ожидание M[X/Y=30).
M[X/Y=y] = 11*0 + 16*0.67 + 21*0.33 + 26*0 + 31*0 + 36*0 = 17.67
Условная дисперсия D[X/Y=30).
D[X/Y=y] = 11 2 *0 + 16 2 *0.67 + 21 2 *0.33 + 26 2 *0 + 31 2 *0 + 36 2 *0 — 17.67 2 = 5.56
Условный закон распределения X(Y=40).
P(X=11/Y=40) = 0/55 = 0
P(X=16/Y=40) = 0/55 = 0
P(X=21/Y=40) = 6/55 = 0.11
P(X=26/Y=40) = 45/55 = 0.82
P(X=31/Y=40) = 4/55 = 0.0727
P(X=36/Y=40) = 0/55 = 0
Условное математическое ожидание M[X/Y=40).
M[X/Y=y] = 11*0 + 16*0 + 21*0.11 + 26*0.82 + 31*0.0727 + 36*0 = 25.82
Условная дисперсия D[X/Y=40).
D[X/Y=y] = 11 2 *0 + 16 2 *0 + 21 2 *0.11 + 26 2 *0.82 + 31 2 *0.0727 + 36 2 *0 — 25.82 2 = 4.51
Условный закон распределения X(Y=50).
P(X=11/Y=50) = 0/16 = 0
P(X=16/Y=50) = 0/16 = 0
P(X=21/Y=50) = 2/16 = 0.13
P(X=26/Y=50) = 8/16 = 0.5
P(X=31/Y=50) = 6/16 = 0.38
P(X=36/Y=50) = 0/16 = 0
Условное математическое ожидание M[X/Y=50).
M[X/Y=y] = 11*0 + 16*0 + 21*0.13 + 26*0.5 + 31*0.38 + 36*0 = 27.25
Условная дисперсия D[X/Y=50).
D[X/Y=y] = 11 2 *0 + 16 2 *0 + 21 2 *0.13 + 26 2 *0.5 + 31 2 *0.38 + 36 2 *0 — 27.25 2 = 10.94
Условный закон распределения X(Y=60).
P(X=11/Y=60) = 0/14 = 0
P(X=16/Y=60) = 0/14 = 0
P(X=21/Y=60) = 0/14 = 0
P(X=26/Y=60) = 4/14 = 0.29
P(X=31/Y=60) = 7/14 = 0.5
P(X=36/Y=60) = 3/14 = 0.21
Условное математическое ожидание M[X/Y=60).
M[X/Y=y] = 11*0 + 16*0 + 21*0 + 26*0.29 + 31*0.5 + 36*0.21 = 30.64
Условная дисперсия D[X/Y=60).
D[X/Y=y] = 11 2 *0 + 16 2 *0 + 21 2 *0 + 26 2 *0.29 + 31 2 *0.5 + 36 2 *0.21 — 30.64 2 = 12.37
3. Условный закон распределения Y.
Условный закон распределения Y(X=11).
P(Y=20/X=11) = 2/2 = 1
P(Y=30/X=11) = 0/2 = 0
P(Y=40/X=11) = 0/2 = 0
P(Y=50/X=11) = 0/2 = 0
P(Y=60/X=11) = 0/2 = 0
Условное математическое ожидание M[Y/X=11).
M[Y/X=x] = 20*1 + 30*0 + 40*0 + 50*0 + 60*0 = 20
Условная дисперсия D[Y/X=11).
D[Y/X=x] = 20 2 *1 + 30 2 *0 + 40 2 *0 + 50 2 *0 + 60 2 *0 — 20 2 = 0
Условный закон распределения Y(X=16).
P(Y=20/X=16) = 4/10 = 0.4
P(Y=30/X=16) = 6/10 = 0.6
P(Y=40/X=16) = 0/10 = 0
P(Y=50/X=16) = 0/10 = 0
P(Y=60/X=16) = 0/10 = 0
Условное математическое ожидание M[Y/X=16).
M[Y/X=x] = 20*0.4 + 30*0.6 + 40*0 + 50*0 + 60*0 = 26
Условная дисперсия D[Y/X=16).
D[Y/X=x] = 20 2 *0.4 + 30 2 *0.6 + 40 2 *0 + 50 2 *0 + 60 2 *0 — 26 2 = 24
Условный закон распределения Y(X=21).
P(Y=20/X=21) = 0/11 = 0
P(Y=30/X=21) = 3/11 = 0.27
P(Y=40/X=21) = 6/11 = 0.55
P(Y=50/X=21) = 2/11 = 0.18
P(Y=60/X=21) = 0/11 = 0
Условное математическое ожидание M[Y/X=21).
M[Y/X=x] = 20*0 + 30*0.27 + 40*0.55 + 50*0.18 + 60*0 = 39.09
Условная дисперсия D[Y/X=21).
D[Y/X=x] = 20 2 *0 + 30 2 *0.27 + 40 2 *0.55 + 50 2 *0.18 + 60 2 *0 — 39.09 2 = 44.63
Условный закон распределения Y(X=26).
P(Y=20/X=26) = 0/57 = 0
P(Y=30/X=26) = 0/57 = 0
P(Y=40/X=26) = 45/57 = 0.79
P(Y=50/X=26) = 8/57 = 0.14
P(Y=60/X=26) = 4/57 = 0.0702
Условное математическое ожидание M[Y/X=26).
M[Y/X=x] = 20*0 + 30*0 + 40*0.79 + 50*0.14 + 60*0.0702 = 42.81
Условная дисперсия D[Y/X=26).
D[Y/X=x] = 20 2 *0 + 30 2 *0 + 40 2 *0.79 + 50 2 *0.14 + 60 2 *0.0702 — 42.81 2 = 34.23
Условный закон распределения Y(X=31).
P(Y=20/X=31) = 0/17 = 0
P(Y=30/X=31) = 0/17 = 0
P(Y=40/X=31) = 4/17 = 0.24
P(Y=50/X=31) = 6/17 = 0.35
P(Y=60/X=31) = 7/17 = 0.41
Условное математическое ожидание M[Y/X=31).
M[Y/X=x] = 20*0 + 30*0 + 40*0.24 + 50*0.35 + 60*0.41 = 51.76
Условная дисперсия D[Y/X=31).
D[Y/X=x] = 20 2 *0 + 30 2 *0 + 40 2 *0.24 + 50 2 *0.35 + 60 2 *0.41 — 51.76 2 = 61.59
Условный закон распределения Y(X=36).
P(Y=20/X=36) = 0/3 = 0
P(Y=30/X=36) = 0/3 = 0
P(Y=40/X=36) = 0/3 = 0
P(Y=50/X=36) = 0/3 = 0
P(Y=60/X=36) = 3/3 = 1
Условное математическое ожидание M[Y/X=36).
M[Y/X=x] = 20*0 + 30*0 + 40*0 + 50*0 + 60*1 = 60
Условная дисперсия D[Y/X=36).
D[Y/X=x] = 20 2 *0 + 30 2 *0 + 40 2 *0 + 50 2 *0 + 60 2 *1 — 60 2 = 0
Ковариация.
cov(X,Y) = M[X·Y] — M[X]·M[Y]
cov(X,Y) = (20·11·2 + 20·16·4 + 30·16·6 + 30·21·3 + 40·21·6 + 50·21·2 + 40·26·45 + 50·26·8 + 60·26·4 + 40·31·4 + 50·31·6 + 60·31·7 + 60·36·3)/100 — 25.3 · 42.3 = 38.11
Если случайные величины независимы, то их ковариации равна нулю. В нашем случае cov(X,Y) ≠ 0.
Коэффициент корреляции.
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
Найдем необходимые числовые характеристики.
Выборочные средние:
x = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 42.3
y = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 25.3
Дисперсии:
σ 2 x = (20 2 (2 + 4) + 30 2 (6 + 3) + 40 2 (6 + 45 + 4) + 50 2 (2 + 8 + 6) + 60 2 (4 + 7 + 3))/100 — 42.3 2 = 99.71
σ 2 y = (11 2 (2) + 16 2 (4 + 6) + 21 2 (3 + 6 + 2) + 26 2 (45 + 8 + 4) + 31 2 (4 + 6 + 7) + 36 2 (3))/100 — 25.3 2 = 24.01
Откуда получаем среднеквадратические отклонения:
σx = 9.99 и σy = 4.9
и ковариация:
Cov(x,y) = (20·11·2 + 20·16·4 + 30·16·6 + 30·21·3 + 40·21·6 + 50·21·2 + 40·26·45 + 50·26·8 + 60·26·4 + 40·31·4 + 50·31·6 + 60·31·7 + 60·36·3)/100 — 42.3 · 25.3 = 38.11
Определим коэффициент корреляции:
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.38 x + 9.14
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 1.59 y + 2.15
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (42.3; 25.3) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=100-m-1 = 98 находим tкрит:
tкрит (n-m-1;α/2) = (98;0.025) = 1.984
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
Задание. Количество попаданий пар значений случайных величин X и Y в соответствующие интервалы приведены в таблице. По этим данным найти выборочный коэффициент корреляции и выборочные уравнения прямых линий регрессии Y на X и X на Y .
Решение
Пример. Распределение вероятностей двумерной случайной величины (X, Y) задано таблицей. Найти законы распределения составляющих величин X, Y и коэффициент корреляции p(X, Y).
Скачать решение
Задание. Двумерная дискретная величина (X, Y) задана законом распределения. Найти законы распределения составляющих X и Y, ковариацию и коэффициент корреляции.
🎬 Видео
Функция распределения и плотность распределенияСкачать

Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минутСкачать

Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

Теория вероятностей #14: математ. ожидание, дисперсия, медиана, мода, начальные моментыСкачать

Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать

Математическое ожидание дискретной случайной величины. 10 класс.Скачать

Двумерное дискретное распределениеСкачать

Функция распределения дискретной случайной величиныСкачать

2.8. Совместное распределение двух случайных величин.Скачать

Условные и безусловные распределенияСкачать

Математическое ожидание дискретной случайной величиныСкачать

Нахождение функции распределения для двумерного случайного вектора по плотностиСкачать

Дисперсия случайной величины/Как найти?Скачать

Математическое ожидание, дисперсия, среднее квадратическое отклонение НСВСкачать