Около правильного многоугольника можно описать более 1 окружности (7 видео)

Около правильного многоугольника можно описать более 1 окружности

Какие из следующих утверждений верны?

1) Около любого правильного многоугольника можно описать не более одной окружности.

2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

4) Около любого ромба можно описать окружность.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Около любого правильного многоугольника можно описать не более одной окружности.»— верно, около любого правильного многоугольника можно описать окружность, и притом только одну.

2) «Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.» — верно, треугольник с такими сторонами является прямоугольным, таким образом, центр окружности лежит на гипотенузе.

3) «Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.» — верно, диагонали квадрата точкой пересечения делятся пополам, таким образом, центром окружности является точка пресечения диагоналей.

4) «Около любого ромба можно описать окружность.» — неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.

Содержание

Окружность, описанная около правильного многоугольника
Доказательство
Правильные многоугольники
Понятие правильного многоугольника
Теорема об описанной около правильного многоугольника окружности
Готовые работы на аналогичную тему
Теорема вписанной в правильный многоугольник окружности
Формулы для правильного многоугольника
Пример задачи на понятие правильного многоугольника
🎦 Видео

Видео:110. Окружность, описанная около правильного многоугольникаСкачать

Окружность, описанная около правильного многоугольника

Теорема

Около любого правильного многоугольника можно описать окружность, и притом только одну.

Доказательство

Дано: А₁А₂А₃. А_n — правильный многоугольник.

Доказательство:

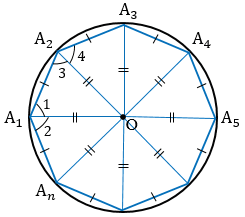
Пусть точка О — точка пересечения биссектрис углов А₁ и А₂. Соединим точку О отрезками с остальными вершинами многоугольника и докажем, что ОА₁ = ОА₂ = . = ОА_n.

А₁А₂А₃. А_n — правильный многоугольник, значит, А₁ = А₂, тогда 1 = 3 (т.к. ОА₁ и ОА₂ биссектрисы равных углов А₁ и А₂), следовательно,

А₁ОА₂ — равнобедренный (по признаку равнобедренного треугольника), поэтому ОА₁ = ОА₂.

А₁ОА₂ = А₂ОА₃ по двум сторонам и углу между ними (А₁А₂ = А₂А₃ как стороны правильного многоугольника, ОА₂ — общая, 3 = 4, т.к. ОА₂ биссектриса угла А₂), следовательно,

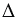
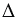
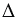
ОА₁ = ОА₃. Аналогично можно доказать, что ОА₂ = ОА₄, ОА₃ = ОА₅ и т.д.

Итак, ОА₁ = ОА₂ = . = ОА_n, значит, точка О равноудалена от всех вершин многоугольника. Поэтому окружность с центром О и радиусом ОА₁ является описанной около многоугольника А₁А₂А₃. А_n.

Докажем, что описать можно только одну окружность.

Рассмотрим какие-нибудь три вершины многоугольника А₁А₂А₃. А_n, например, А₁, А₂, А₃. Мы можем начертить только одну окружность одновременно проходящую через три точки А₁, А₂, А₃ (смотри доказательство), т.е. другой окружности проходящей через три данные точки не существует, значит, около многоугольника А₁А₂А₃. А_n можно описать только одну окружность, т.к. точки А₁, А₂, А₃ — вершины данного многоугольника. Теорема доказана.

Поделись с друзьями в социальных сетях:

Видео:9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Правильные многоугольники

Вы будете перенаправлены на Автор24

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Понятие правильного многоугольника

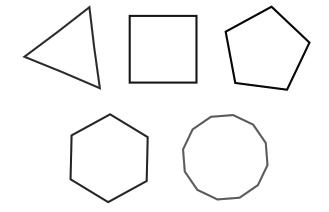
Правильный многоугольник — выпуклый многоугольник, у которого все стороны и все углы равны между собой (Рис. 1).

Рисунок 1. Правильные многоугольники

Как мы знаем, сумма углов многоугольника находится по формуле$(n-2)cdot ^0$

Значит, градусная мера одного угла правильного многоугольника равняется

Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Теорема об описанной около правильного многоугольника окружности

Около любого правильного многоугольника можно описать единственную окружность.

Доказательство.

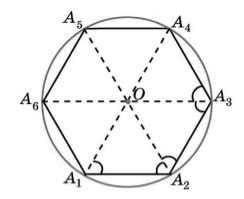
Существование. Пусть нам дан правильный многоугольник $A_1A_2A_3dots A_n$. Пусть биссектрисы углов $A_1 и A_2$ пересекаются в точке $O$. Соединим с этой точкой все остальные вершины правильного многоугольника (Рис. 2).

Рисунок 2. Описанная вокруг правильного многоугольника окружность

Так как углы $A_1 и A_2$ равны и $A_1O и A_2O$ — биссектрисы, то угол $OA_1A_2$ равен углу $O_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.

Так как $A_1A_2=A_2A_3$, $angle O _1=angle O _3$ и сторона $A_2O$ — общая, то треугольники $O _1$ и $O _3$ равны. Следовательно, $OA_2=OA_3$.

Аналогично доказывают другие равенства. В результате, будем иметь

То есть точка $O$ равноудалена от всех вершин многоугольника, а, значит, точка $O$ — центр описанной вокруг правильного многоугольника окружности.

Единственность. Рассмотрим три вершины многоугольника. Очевидно, что через них проходит только одна окружность, следовательно, вокруг правильного многоугольника можно описать только одну окружность.

Готовые работы на аналогичную тему

Теорема доказана.

Видео:Правильный многоугольник. Окружность, описанная около правильного многоугольника.Скачать

Теорема вписанной в правильный многоугольник окружности

В любой правильный многоугольник можно вписать единственную окружность.

Доказательство.

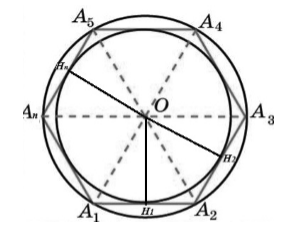
Пусть нам дан правильный многоугольник $A_1A_2A_3dots A_n$. Пусть точка $O$ — центр описанной вокруг данного многоугольника окружности (Рис. 3).

Рисунок 3. Вписанная в правильный многоугольник окружность

Так как $A_1A_2=A_2A_3$, $angle O _1=angle O _3$ и сторона $A_2O$ — общая, то треугольники $O _1$ и $O _3$ равны.

Аналогично доказывается равенство других треугольников. То есть, мы получим

Значит и высоты этих треугольников равны между собой

Тогда окружность с центром в точке $O$ и радиусом, равным $_1$ проходит через точки $H_1, H_2,dots ,H_n$, то есть касается всех сторон данного многоугольника. Следовательно. Является вписанной для правильного многоугольника.

Единственность. Предположим противное. Пусть существует еще одна вписанная в этот многоугольник окружность. Обозначим её центр $O’$. Тогда $O’$ равноудалена от всех сторон многоугольника, а значит лежит в точке пересечения биссектрис его углов. Но тогда точка $O’$ совпадает с точкой $O$ и, следовательно, эти окружности также совпадают.

Теорема доказана.

Из этих двух теорем можно сформулировать следующие следствия:

Следствие 1: Вписанная в правильный многоугольник окружность касается его в серединах его сторон.

Следствие 2: Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.

Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Формулы для правильного многоугольника

Дадим теперь несколько формул, относящихся к понятию правильного многоугольника (без их вывода).

Введем следующие обозначения. Пусть $S$ — площадь правильного многоугольника, $P$ — периметр правильного многоугольника, $a$ — сторона правильного многоугольника, $r$ — радиус вписанной в правильный многоугольник окружности, $R$ — радиус описанной около правильного многоугольника окружности. Тогда

Видео:Окружность, описанная около правильного многоугольника | Геометрия 7-9 класс #105 | ИнфоурокСкачать

Пример задачи на понятие правильного многоугольника

Чему равна сумма внешних углов правильного $n$-угольника. Если при каждой вершине взят только один внешний угол.

Решение.

Очевидно, что все внешние углы будут равны между собой и их количество равно $n$. Найдем один из них. Внешний угол $beta $ многоугольника будет смежным с внутренним углом многоугольника. Используя формулу нахождения угла правильного $n$-угольника $alpha =frac<^0(n-2)>$, получим

Значит, сумма всех внешних углов равна

Ответ: $^0.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15 04 2021