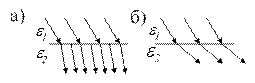напряженность потенциал электрического поля
Электрическое поле создано заряженной металлической сферой с центром в точке О радиуса R1 = 2 см с поверхностной плотностью заряда σ = 2 нКл/см 2 . Точка А находится на расстоянии r1 = 2 см от поверхности сферы. Определить: 1) величину и направление напряженности и потенциал электрического поля в точке А: 2) величину и направление силы, действующей на заряд q = 2/3 нКл помещенный в эту точку поля; 3) работу, совершаемую силами, перемещающими заряд q из точки А в точку В, отстоящую от поверхности шара на r = 4 см; 4) поток вектора напряженности через сферу радиуса R2 = 1 см с центром в точке О. Диэлектрическая проницаемость среды ε = 6.
Две сферы с радиусами R1 = r и R2 = r/2 заряжены с одинаковой постоянной по поверхности плотностью заряда σ. Причем первая сфера имеет положительный, а вторая отрицательный заряд. Сферы расположены так, что их поверхности почти соприкасаются. Найти: 1) Напряженность и потенциал электрического поля в центре первой сферы. 2) Положение точки, в которой напряженность равна 0.
Сферы, изображенные на рис 14.1, имеют радиусы по 0,05 м и заряды q1 = -46 мкКл и q2 = 46 мкКл, которые равномерно распределены по их поверхностям. Расстояние между центрами сфер 20 см. Рассчитать напряженность и потенциал электрического поля в точке D, которая находится внутри отрицательно заряженной сферы в непосредственной близости от ее стенки.
Два положительных точечных заряда сближаются, «скользя» по дуге полуокружности с центром в т.О (от диаметрального расположения к вершине дуги).
Как при этом изменяются напряженность и потенциал электрического поля в т.O?
Точенный заряд, находящийся на вершине полусферы, «растекается» по ее поверхности. Как при этом изменятся напряженность и потенциал электрического поля в центре основания полусферы?
Диэлектрический шар (ε>1), заряженный по объему равномерно и положительно, расположен в вакууме. Как изменяются с увеличением расстояния от центра шара напряженность и потенциал электрического поля?
Две концентрические сферы радиусами 4 и 13 см обладают зарядами -7 и -17 мкКл соответственно. Определить модуль напряженности и потенциал электрического поля в точках, расположенных на расстояниях 1) 3,2 см, 2) 9,4 см, 3) 16 см от общего центра сфер. Сделать поясняющий рисунок. Построить графики зависимости Е(х) и φ(x).
Пространство между двумя концентрическими сферами радиусов R1 и R2 заряжено с объемной плотностью заряда ρ = α/r 2 , где α — постоянная величина. Определить полный заряд q, а также модуль Е напряженности и потенциал φ электрического поля как функции расстояния r от центра сферы.
В вершинах прямоугольного треугольника (стороны которого а:b:с = 5:4:3) расположены одинаковые заряды q. Найти вектор напряженности и потенциал электрического поля в точке, лежащей на середине гипотенузы. Длина гипотенузы 10 см, величина зарядов q = 1 нКл. Определить энергию системы зарядов.
Точечные заряды q1 = q2 = q3 = q4 = q5 = q6 = q расположены в вершинах правильного шестиугольника со стороной 1 см. Найти вектор напряженности и потенциал электрического поля в центре шестиугольника, если величина q = –1 нКл. Определить энергию системы этих зарядов.
Определить напряженность и потенциал электрического поля в центре 0 квадрата (рис. 8.3), в вершинах которого находятся заряды Q1, Q2, Q3 и Q4, а также энергию взаимодействия данной системы зарядов. Сторона квадрата а = 5 см, величины зарядов указаны в табл. 8.1 в соответствии с номером задачи. Q1 = 5, Q2 = 2, Q3 = 1, Q4 = –4 нКл.
В трех вершинах квадрата расположены одинаковые по величине точечные заряды (q1 = q2 = q3 = 1 нКл). Определить 1) напряженность и потенциал электрического поля в четвертой вершине квадрата; 2) энергию системы зарядов. Сторона квадрата равна 1 см.
Точечные заряды Q1 = 1 нКл, Q2 = 1 нКл, Q3 = –1 нКл, Q4 = –1 нКл расположены на плоскости в узлах решетки с ячейкой в форме квадрата со стороной а = 0,1 м. Узлы решетки, в которых находятся указанные заряды, заданы радиус-векторами r1 = (0, 0), r2 = (0, a), r3 = (–a, a), r4 = (–a, 0). В остальных узлах заряды отсутствуют. Определить напряженность и потенциал электрического поля в точке r = (–a, –а), r = (0, –a). Сделайте поясняющий чертеж.
Точечные заряды Q1 = 2 нКл, Q2 = –1 нКл, Q3 = –1 нКл, расположены на плоскости в узлах решетки с ячейкой в форме квадрата со стороной а = 0,1 м. Узлы решетки, в которых находятся указанные заряды, заданы радиус-векторами r1 = (0, 0), r2 = (a, 0), r3 = (0, а). В остальных узлах заряды отсутствуют. Определить напряженность и потенциал электрического поля в точке r = (a, а). Сделайте поясняющий чертеж.
Точечные заряды Q1 = 1 нКл, Q2 = 1 нКл, Q3 = –2 нКл расположены на плоскости в узлах решетки с ячейкой в форме квадрата со стороной а = 0,1 м. Узлы решетки, в которых находятся указанные заряды, заданы радиус-векторами r1 = (0, a), r2 = (0, –а), r3 = (А, 0). В остальных узлах заряды отсутствуют. Определить напряженность и потенциал электрического поля в точке r = (–a, 0). Сделайте поясняющий чертеж.
В вершинах квадрата со стороной а = 2 см расположены два положительных и два отрицательных заряда; абсолютное значение каждого из них Q = 1 нКл. Определить напряженность Е электрического поля и потенциал в точке А (середина боковой стороны) в вакууме.
Видео:Задача №2. Потенциал проводящей сферы.Скачать

Основные типы задач и методы их решения
171-2007
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к решению задач по электростатике и постоянному току
по дисциплине “Общая физика”
для студентов физико-технического факультета
очной формы обучения
Составители: канд. физ.-мат. наук А.Г. Москаленко, канд. физ.-мат. наук Н.В. Матовых, канд. техн. наук М.Н. Гаршина, канд. физ.-мат. наук Е.П. Татьянина, канд. физ.-мат. наук В.С. Железный.
Методические указания к решению задач по электростатике и постоянному току по дисциплине «Общая физика» для студентов физико-технического факультета очной формы обучения / ГОУВПО «Воронежский государственный технический университет»; сост. А.Г. Москаленко, Н.В. Матовых, М.Н. Гаршина, Е.П. Татьянина, В.С. Железный. Воронеж, 2007. 46 с.
В методических указаниях кратко изложен теоретический материал, представлены классификация и методы решения задач, рассмотрены примеры решения типовых задач, соответствующих программе общего курса физики. По каждой теме имеются контрольные вопросы и задачи для самостоятельного решения.
Методические указания предназначены для студентов физико-технического факультета.
Библиограф.: 6 назв.
Рецензент канд. физ.-мат. наук, доц. А.Ф. Татаренков
Ответственный за выпуск зав. кафедрой,
профессор В.С. Железный
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

технический университет», 2007
Электростатическое поле в вакууме
Основные законы и формулы
1.Напряженность и потенциал поля точечного заряда




Принцип суперпозиции электростатических полей


2. Линейная, поверхностная и объемная плотность зарядов


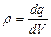
3. Теорема Гаусса для электростатического поля в вакууме

4. Связь между напряженностью и потенциалом электростатического поля.


5. Циркуляция вектора напряженности

6. Работа сил электростатического поля


7. Напряженность и потенциал поля диполя
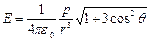

где p = 

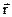

8. Сила и момент сил, действующих на диполь во внешнем поле:

Качественные задачи
1. В центре воображаемой сферы находится точечный заряд. Изменится ли поток вектора 
 | 2. Является ли эквипотенциальной плоскость симметрии  в поле точечных зарядов: q1=q2=q; б) q1=+q; q2=-q? в поле точечных зарядов: q1=q2=q; б) q1=+q; q2=-q? |
 | 3. Вблизи равномерно заряженной нити построим замкнутую поверхность, имеющую форму цилиндра, соосного с нитью. Как изменится модуль потока вектора  через полную поверхность цилиндра, если нить наклонить? через полную поверхность цилиндра, если нить наклонить? |
 | 4.Четыре точечных заряда расположены в вершинах квадрата. Указать направление максимального возрастания потенциала в центре квадрата. |
 | 5. Два точечных заряда сближаются, скользя по дуге окружности с центром О. Как при этом изменяются  и и 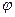 в точке О. в точке О. |
6. Заряды 


7. Заряд 



8. Напряженность поля 


Основные типы задач и методы их решения
1. Определение напряженности и потенциала заданного распределения точечных зарядов.
Метод решения. Прямое суммирование выражений для потенциала и напряженности электростатического поля каждого заряда из заданного распределения точечных зарядов:

2.Определение потенциала и напряженности электростатического поля заданного непрерывного распределения линейных, поверхностных или объемных зарядов.
Метод решения. Интегрирование выражений для потенциала и напряженности поля заданного непрерывного распределения заряда:

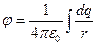
где 


3. Определение напряженности электростатического поля и потенциала заданного непрерывного распределения зарядов, обладающих плоской, осевой или центральной симметрией.
Метод решения. Применение теоремы Гаусса и формулы, связывающей напряженность поля и потенциал:


б) Примеры решения задач
I. В вершинах квадрата со стороной 
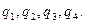
а) 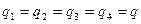
б) 

в) 

 |
Напряженность поля и потенциал системы точечных зарядов определяются соотношениями

Учитывая, что 




получаем 



а) если 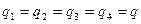
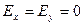

б) если 

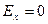


в) если 

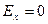


2. Положительный заряд равномерно распределен по тонкому кольцу радиусом 





Выделим на кольце около точки А элемент 


В силу симметрии вектор 

Учитывая, что 

получаем 

а) Если 

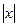

т.е. на больших расстояниях эта система ведет себя как точечный заряд.
3. Тонкая прямая нить длиной 2 




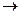




Из соображений симметрии ясно, что

Приведем это выражение к виду, удобному для интегрирования. Из рисунка видно, что

Поэтому 
где 
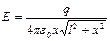
а) Если х>> 


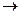


4. Очень тонкий диск равномерно заряжен с поверхностной плотностью 






В данном случае 



Заметим, что на больших расстояниях от диска

где 


В непосредственной же близости от точки 0 телесный угол 

5. Две концентрические сферы с радиусами 







Поле такой системы центрально-симметричное, поэтому используем теорему Гаусса и в качестве замкнутой поверхности выберем концентрическую сферу радиусом 
Для 


и 
Для определения потенциала используем связь между 
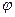


Для 




Для
Видео:Закон КулонаСкачать

Электростатическое поле в вакууме
171-2007
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к решению задач по электростатике и постоянному току
по дисциплине “Общая физика”
для студентов физико-технического факультета
очной формы обучения
Составители: канд. физ.-мат. наук А.Г. Москаленко, канд. физ.-мат. наук Н.В. Матовых, канд. техн. наук М.Н. Гаршина, канд. физ.-мат. наук Е.П. Татьянина, канд. физ.-мат. наук В.С. Железный.
Методические указания к решению задач по электростатике и постоянному току по дисциплине «Общая физика» для студентов физико-технического факультета очной формы обучения / ГОУВПО «Воронежский государственный технический университет»; сост. А.Г. Москаленко, Н.В. Матовых, М.Н. Гаршина, Е.П. Татьянина, В.С. Железный. Воронеж, 2007. 46 с.
В методических указаниях кратко изложен теоретический материал, представлены классификация и методы решения задач, рассмотрены примеры решения типовых задач, соответствующих программе общего курса физики. По каждой теме имеются контрольные вопросы и задачи для самостоятельного решения.
Методические указания предназначены для студентов физико-технического факультета.
Библиограф.: 6 назв.
Рецензент канд. физ.-мат. наук, доц. А.Ф. Татаренков
Ответственный за выпуск зав. кафедрой,
профессор В.С. Железный
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета

технический университет», 2007
Электростатическое поле в вакууме
Основные законы и формулы
1.Напряженность и потенциал поля точечного заряда


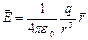
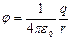
Принцип суперпозиции электростатических полей

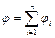
2. Линейная, поверхностная и объемная плотность зарядов
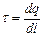
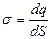

3. Теорема Гаусса для электростатического поля в вакууме

4. Связь между напряженностью и потенциалом электростатического поля.

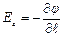
5. Циркуляция вектора напряженности
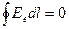
6. Работа сил электростатического поля


7. Напряженность и потенциал поля диполя


где p = 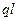
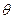

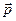
8. Сила и момент сил, действующих на диполь во внешнем поле:

Качественные задачи
1. В центре воображаемой сферы находится точечный заряд. Изменится ли поток вектора 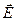
 | 2. Является ли эквипотенциальной плоскость симметрии 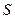 в поле точечных зарядов: q1=q2=q; б) q1=+q; q2=-q? в поле точечных зарядов: q1=q2=q; б) q1=+q; q2=-q? |
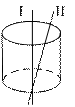 | 3. Вблизи равномерно заряженной нити построим замкнутую поверхность, имеющую форму цилиндра, соосного с нитью. Как изменится модуль потока вектора  через полную поверхность цилиндра, если нить наклонить? через полную поверхность цилиндра, если нить наклонить? |
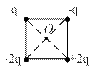 | 4.Четыре точечных заряда расположены в вершинах квадрата. Указать направление максимального возрастания потенциала в центре квадрата. |
 | 5. Два точечных заряда сближаются, скользя по дуге окружности с центром О. Как при этом изменяются 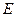 и и  в точке О. в точке О. |
6. Заряды 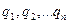
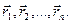

7. Заряд 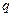
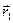
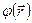

8. Напряженность поля 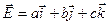
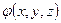
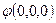
Проводники и диэлектрики в электрическом поле
Основные законы и формулы
1. Поляризованность диэлектрика
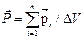
где 
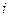
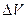
2. Связь между поляризованностью диэлектрика и напряженностью электростатического поля

где χ — диэлектрическая восприимчивость вещества.
3. Вектор электрического смещения
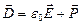
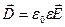
где 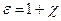
4. Теорема Гаусса для электростатического поля в диэлектрике
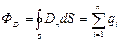
где 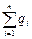
5. Условия на границе раздела двух диэлектриков

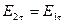
6. Поле в однородном диэлектрике
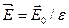
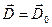
где 
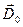
7. Напряженность электростатического поля у поверхности проводника 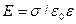
где 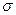
Качественные задачи
 | 1. Точечный заряд 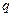 находится внутри незаряженной металлической полости находится внутри незаряженной металлической полости  . Для каких замкнутых поверхностей (а, б, в) поток вектора . Для каких замкнутых поверхностей (а, б, в) поток вектора 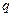 равен нулю? равен нулю? |
 | 2. Точечный заряд 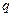 находится в центре диэлектрического шара. Отличны ли от нуля интегралы: a) находится в центре диэлектрического шара. Отличны ли от нуля интегралы: a)  ; б) ; б) 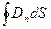 по замкнутой поверхности S, частично захватывающей диэлектрик? по замкнутой поверхности S, частично захватывающей диэлектрик? |
3. В центре воображаемой сферы находится точечный заряд. Изменится ли поток вектора 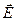
а) все пространство заполнить однородным и изотропным диэлектриком;
б) заменить сферическую поверхность кубической с центром в заряде?
4. В области, ограниченной заземленной металлической оболочкой, находится заряд. Определить: а) есть ли электрическое поле вне оболочки; б) будет ли действовать электрическая сила на другой заряд, помещенный вблизи наружной поверхности оболочки.
5. По представленным рисункам определить, с помощью каких линий ( 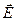


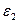
Основные законы и формулы
1. Электроемкость уединенного проводника и конденсатора
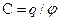
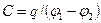
2. Емкость плоского конденсатора

где 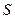
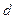
3. Емкость цилиндрического конденсатора
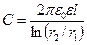
где 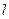
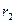
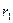
3. Емкость сферического конденсатора.

где 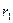
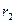
4. Емкость системы конденсаторов при последовательном и параллельном соединении
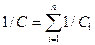

5. Энергия взаимодействия системы точечных зарядов
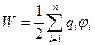
где 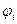

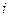
6. Полная энергия системы с непрерывным распределением заряда
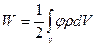
7. Энергия заряженного конденсатора

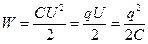
8. Объемная плотность энергии электрического поля
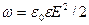
Качественные задачи
1. Заряд уединенного металлического шара, находящегося в вакууме, равен 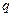



3. Заряженный уединенный конденсатор присоединяют параллельно к такому же незаряженному. Какие из приведенных параметров первого конденсатора уменьшаются вдвое: а) заряд, б) напряженность, в) напряжение, г) энергия?
4. Пластины плоского воздушного конденсатора соединенного с источником постоянной ЭДС, медленно раздвигают с постоянной скоростью. Как при этом изменяется сила тока в цепи?
5. Как изменится напряжение в конденсаторе, если в него внести металлическую пластинку толщиной, равной половине расстояния между обкладками конденсатора?
Основные законы и формулы
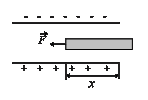
1. Сила и плотность электрического тока
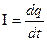
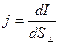
2. Плотность тока в проводнике
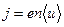
где — средняя скорость упорядоченного движения зарядов; n – концентрация зарядов.
3. Сопротивление проводника

где ρ – удельное сопротивление;

4. Обобщенный закон Ома в дифференциальной и интегральной формах
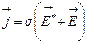

где 
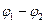
5. Закон Джоуля-Ленца в дифференциальной и интегральной формах
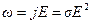
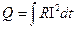
где ω – удельная тепловая мощность тока.
6. Правила Кирхгофа
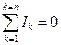
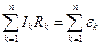
🔍 Видео
НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать

Урок 224. Напряженность поля неточечных зарядовСкачать

Выполнялка 157 . Электростатика.Два точечных зарядаСкачать

Выполнялка 89.Задача на нахождение НапряженностиСкачать

Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Поле заряженного кольцаСкачать

Урок 218. Напряженность электрического поляСкачать

Билет №02 "Теорема Гаусса"Скачать

Билет №03 "Потенциал"Скачать

Нахождение результирующего значения напряженности электрического поля - (0151) 1 частьСкачать

электростатика 🔹 ЗАКОН КУЛОНА 🔹 РЕШЕНИЕ ЗАДАЧСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

3.14Скачать

Физика С какой силой взаимодействуют два точечных заряда 2 и 4 нКл, находящиеся на расстоянии 3 смСкачать

Лекция 2-2 Потенциал - примерыСкачать

Потенциал электрического поля. 10 класс.Скачать

Потенциал сферы и проводящего шараСкачать

39. Принцип суперпозицииСкачать