О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
- Основные понятия
- Формула радиуса окружности
- Если известна площадь круга
- Если известна длина
- Если известен диаметр окружности
- Если известна диагональ вписанного прямоугольника
- Если известна сторона описанного квадрата
- Если известны стороны и площадь вписанного треугольника
- Если известна площадь и полупериметр описанного треугольника
- Если известна площадь сектора и его центральный угол
- Если известна сторона вписанного правильного многоугольника
- Скачать онлайн таблицу
- Как в сектор вписать окружность
- Как в сектор вписать окружность
- Площадь круга
- Сектор круга. Площадь сектора
- Сегмент. Площадь сегмента
- Окружность: вписанная в многоугольник или угол
- Вписанная окружность
- Свойства вписанной окружности
- В треугольник
- В четырехугольник
- Примеры вписанной окружности
- Верные и неверные утверждения
- Окружность вписанная в угол
- Найдите радиус окружности, вписанной в сектор радиуса 6, периметр которого равен 12 + 2п
- Ваш ответ
- решение вопроса
- Похожие вопросы
Видео:Как найти радиус окружности, вписанной в круговой сектор?Скачать

Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Видео:Сможешь найти радиус окружности вписанной в сектор?Скачать

Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Видео:Площадь сектора и сегмента. 9 класс.Скачать

Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Видео:Радиус описанной окружностиСкачать

Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Видео:Формулы для радиуса окружности #shortsСкачать

Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Как в сектор вписать окружность
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Как в сектор вписать окружность
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:
O — центр круга, OA — радиус круга.
Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
| D = 2r, значит r = | D | . |
| 2 |
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | ) 2 = π | D 2 | = π | D 2 | . |
| 2 | 2 2 | 4 |
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Сектор круга. Площадь сектора
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Формула площади сектора:
| S = | πr 2 | · n = | πr 2 n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
| πr 2 n |
| 360 |
можно представить в виде произведения
| πr 2 n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
| S = | sr | , |
| 2 |
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.
Площадь сегмента AMB будет вычисляться по формуле:
| S = | r | (s — BC), |
| 2 |
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
Видео:Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте СегментаСкачать

Окружность: вписанная в многоугольник или угол
Определения
Окружность (S) вписана в угол (alpha) , если (S) касается сторон угла (alpha) .
Окружность (S) вписана в многоугольник (P) , если (S) касается всех сторон (P) .
В этом случае многоугольник (P) называется описанным около окружности.
Теорема
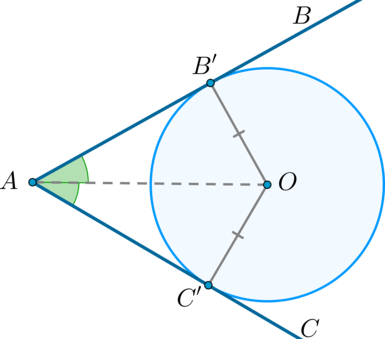
Центр вписанной в угол окружности лежит на его биссектрисе.
Доказательство
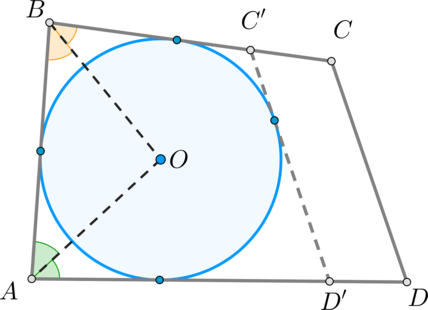
Пусть (O) – центр некоторой окружности, вписанной в угол (BAC) . Пусть (B’) – точка касания окружности и (AB) , а (C’) – точка касания окружности и (AC) , тогда (OB’) и (OC’) – радиусы, проведённые в точки касания, следовательно, (OC’perp AC) , (OB’perp AB) , (OC’ = OB’) .
Значит, треугольники (AC’O) и (AB’O) – прямоугольные треугольники, у которых равны катеты и общая гипотенуза, следовательно, они равны, откуда (angle CAO = angle BAO) , что и требовалось доказать.
Теорема
В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.
Доказательство
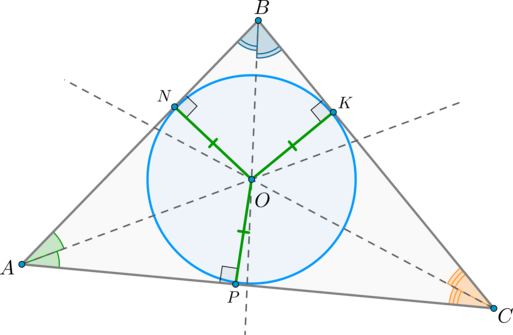
Проведем биссектрисы углов (angle A) и (angle B) . Пусть они пересеклись в точке (O) .
Т.к. (O) лежит на биссектрисе (angle A) , то расстояния от точки (O) до сторон угла равны: (ON=OP) .
Т.к. (O) также лежит на биссектрисе (angle B) , то (ON=OK) . Таким образом, (OP=OK) , следовательно, точка (O) равноудалена от сторон угла (angle C) , следовательно, лежит на его биссектрисе, т.е. (CO) – биссектриса (angle C) .
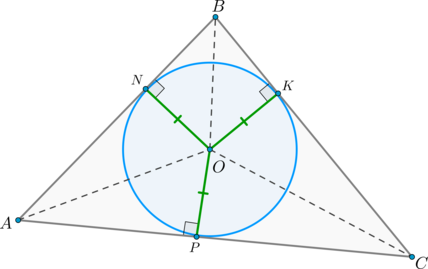
Таким образом, точки (N, K, P) равноудалены от точки (O) , то есть лежат на одной окружности. По определению это и есть вписанная в треугольник окружность.
Данная окружность единственна, т.к. если предположить, что существует другая вписанная в (triangle ABC) окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.
Таким образом, попутно была доказана следующая теорема:
Следствие
Биссектрисы треугольника пересекаются в одной точке.
Теорема о площади описанного треугольника
Если (a,b,c) – стороны треугольника, а (r) – радиус вписанной в него окружности, то площадь треугольника [S_ =pcdot r] где (p=dfrac2) – полупериметр треугольника.
Доказательство
Но (ON=OK=OP=r) – радиусы вписанной окружности, следовательно,
Следствие
Если в многоугольник вписана окружность и (r) – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на (r) : [S_ >=pcdot r]
Теорема
В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.
Доказательство
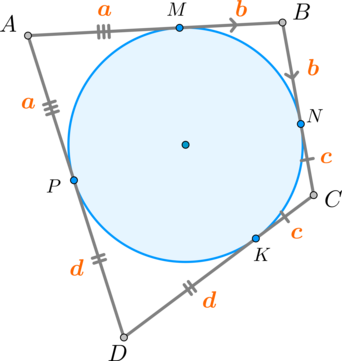
Необходимость. Докажем, что если в (ABCD) вписана окружность, то (AB+CD=BC+AD) .
Пусть (M,N,K,P) – точки касания окружности и сторон четырехугольника. Тогда (AM, AP) – отрезки касательных к окружности, проведенные из одной точки, следовательно, (AM=AP=a) . Аналогично, (BM=BN=b, CN=CK=c, DK=DP=d) .
Достаточность. Докажем, что если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.
Проведем биссектрисы углов (angle A) и (angle B) , пусть они пересекутся в точке (O) . Тогда точка (O) равноудалена от сторон этих углов, то есть от (AB, BC, AD) . Впишем окружность в (angle A) и (angle B) с центром в точке (O) . Докажем, что эта окружность будет касаться и стороны (CD) .
Предположим, что это не так. Тогда (CD) либо является секущей, либо не имеет общих точек с окружностью. Рассмотрим второй случай (первый будет доказываться аналогично).
Проведем касательную прямую (C’D’ parallel CD) (как показано на рисунке). Тогда (ABC’D’) – описанный четырехугольник, следовательно, (AB+C’D’=BC’+AD’) .
Т.к. (BC’=BC-CC’, AD’=AD-DD’) , то:
[AB+C’D’=BC-CC’+AD-DD’ Rightarrow C’D’+CC’+DD’=BC+AD-AB=CD]
Получили, что в четырехугольнике (C’CDD’) сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, (CD) касается окружности.
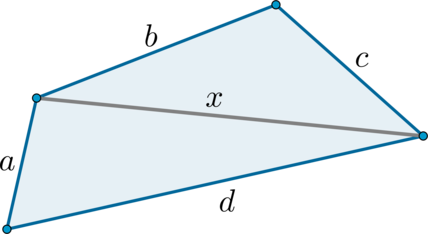
Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.
Т.к. в любом треугольнике сумма двух сторон всегда больше третьей, то (a+x>d) и (b+c>x) . Складывая данные неравенства, получим: (a+x+b+c>d+x Rightarrow a+b+c>d) . Следовательно, сумма любых трех сторон всегда больше четвертой стороны.
Теоремы
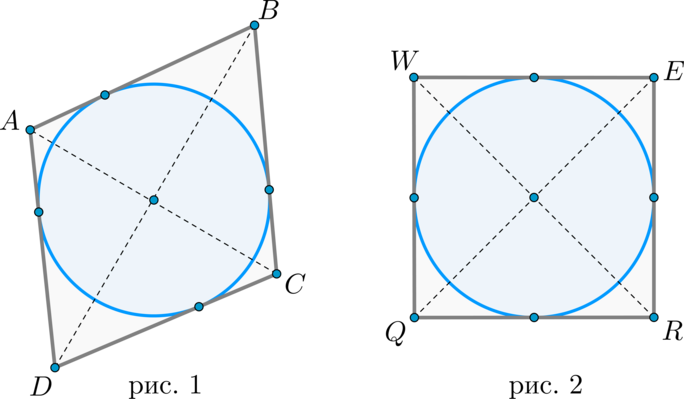
1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).
2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).
Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.
Доказательство
1) Рассмотрим параллелограмм (ABCD) , в который вписана окружность. Тогда (AB+CD=BC+AD) . Но в параллелограмме противоположные стороны равны, т.е. (AB=CD, BC=AD) . Следовательно, (2AB=2BC) , а значит, (AB=BC=CD=AD) , т.е. это ромб.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.
2) Рассмотрим прямоугольник (QWER) . Т.к. прямоугольник является параллелограммом, то согласно первому пункту (QW=WE=ER=RQ) , т.е. это ромб. Но т.к. все углы у него прямые, то это квадрат.
Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac (a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
- Треугольник
- Четырехугольник
- Многоугольник
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Найдите радиус окружности, вписанной в сектор радиуса 6, периметр которого равен 12 + 2п
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,962
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.