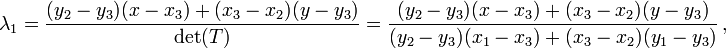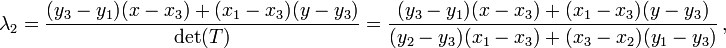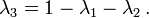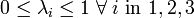Алгоритм для рисования треугольника (7 видео)

Краткий курс компьютерной графики: пишем упрощённый OpenGL своими руками, статья 2 из 6

Содержание

Улучшение кода
Official translation (with a bit of polishing) is available here.
Update:
Рисуем заполненный треугольник
Рисуем модель
Плоская тонировка
Алгоритм для рисования треугольника
Друзья
Растеризация треугольника. Алгоритм заливки (заполнения)
Программирование на C, C# и Java
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Растеризация треугольников на основе барицентрических координат C#
💡 Видео

Улучшение кода

Official translation (with a bit of polishing) is available here.

Update:

Внимание, статья 4в даёт новую, более простую версию растеризатора.

Давайте знакомиться, это я.

То есть, модель моей башки, отрендеренная в программе, которую мы сделаем за ближайшие час-два.

В прошлый раз мы нарисовали проволочную сетку трёхмерной модели, в этот раз мы зальём полигоны. Точнее, треугольники, так как OpenGL практически любой полигон триангулирует, поэтому ни к чему разбирать сложный случай. Напоминаю, что этот цикл статей создан для самостоятельного программирования. Время, которое я здесь привожу — это не время чтения моего кода. Это время написания вашего кода с нуля. Мой код здесь только для того, чтобы сравнить ваш (рабочий) код с моим. Я совсем не являюсь хорошим программистом, поэтому ваш код может быть существенно лучше моего. Любая критика приветствуется, любым вопросам рад.

Пожалуйста, если вы следуете этому туториалу и пишете свой код, выкладывайте его на github.com/code.google.com и им подобные и давайте ссылки в комментариях! Это может хорошо помочь как и вам (другие люди могут чего посоветовать), так и будущим читателям.

Видео:Реактивный треугольник 🔺Скачать

Рисуем заполненный треугольник

Итак, тема на сегодня (примерно на два часа для плохо программирующих, но мотивированных студентов): отрисовка двумерных треугольников. В прошлый раз мы разобрали алгоритм Брезенхэма для растеризации отрезка, теперь задача нарисовать заполненный треугольник. Вы будете смеяться, но это нетривиальная задача. Я не знаю почему, но я знаю, что это так. Большинство моих студентов без подсказок проводят над этой задачей существенно больше пары часов. Давайте определимся с методом, а затем будем программировать.

В самом начале давайте рассмотрим вот такой псевдокод:

Я очень люблю этот метод. Он простой и рабочий. Найти описывающий прямоугольник крайне просто, проверить принадлежность точки двумерному треугольнику (да и любому выпуклому полигону) тоже просто.

Оффтоп: если мне нужно будет написать код, который будет крутиться на, скажем, самолёте, и этот код должен будет проверять принадлежность точки полигону, я никогда не сяду на этот самолёт. Это на удивление сложная проблема, если мы хотим её решить надёжно.

Почему я люблю этот код? Да потому, что, увидев такое, совсем новичок в программировании его воспримет с энтузиазмом, человек, немного знакомый с программированием, только самодовольно хмыкнет, мол, вот идиот писал. А эксперт в программировании компьютерной графики просто пожмёт плечами, мол, ну да, так оно и работает в реальной жизни. Массивно-параллельные вычисления в тысячах маленьких графических процессоров (я говорю про обычные потребительские компьютеры) творят чудеса. Но мы будем писать код под центральный процессор, поэтому этот метод использовать не будем. Да и какая разница, как оно там в кремнии, нашей абстракции вполне хватит для понимания принципа работы.

Окей, начальная заглушка будет выглядеть следующим образом:

Как обычно, на гитхабе доступен отпечаток кода. В этом коде всё просто: я даю три треугольника для начальной отладки вашего кода; если внутри функции triangle просто сделать вызов line(), то получим контур треугольника. Как нарисовать заполненный треугольник?

Хороший метод отрисовки треугольника должен обладать следующими свойствами:

Он должен быть (сюрприз) простым и быстрым
Он должен быть симметричным: картинка не должна зависеть от порядка вершин, переданных в функцию отрисовки
Если два треугольника имеют две общие вершины, между ними не должно быть дырок из-за округлений растеризации.

Требований можно добавлять гораздо больше, но мы довольствуемся этими тремя.

Традиционно используется line sweeping (заметание отрезком?):

Сортируем вершины треугольника по их y-координате
Растеризуем параллельно левую и правую границы треугольника
Отрисовываем горзонтальный отрезок между левой и правой точкой границы

Тут мои студенты начинают теряться, кто левый, кто правый, да и вообще, в треугольнике три отрезка…
В этот момент я оставляю своих студентов примерно на час, чтение моего кода куда как менее ценно, нежели сравнение своего (выстраданного!) кода с моим.

Как рисую я? Ещё раз, если у вас есть лучший метод, то я его с огромным удовольствием возьму на вооружение. Давайте предположим, что у нас есть три точки треугольника, t0,t1,t2, они отсортированы по возрастанию y-координаты.
Тогда граница А будет между t0 и t2, граница Б будет между t0 и t1, а затем между t1 и t2.

Здесь у нас граница А нарисована красным, а граница Б зелёным.

Граница Б, к сожалению, составная. Давайте отрисуем нижнюю половину треугольника, разрезав его по горизонтали в точке излома границы Б.

Заметьте, что в этот раз у меня получились разрывные отрезки. В отличие от прошлого раза (где мы рисовали прямые) я не заморочился поворотом изображения на 90°. Почему? Это оказывается не всем очевидным моментом. Просто если мы соединим горизонтальными линиями соответствующие пары точек, то пробелы пропадут:

Теперь осталось отрисовать вторую половину треугольника. Это можно сделать, добавив второй цикл:

На этом можно было бы успокоиться, но у меня случается несварение, когда я дважды вижу один и тот же код, да ещё так рядом. Поэтому сделаем его чуть менее читаемым, зато более простым для модификаций.

Отпечаток кода для отрисовки 2d треугольников.

Видео:ТРЕУГОЛЬНИК В НЕЙРОГРАФИКЕСкачать

Рисуем модель

Мы умеем уже отрисовывать модель с пустыми треугольниками, давайте их зальём случайным цветом, это поможет нам проверить, насколько хорошо мы закодировали заполнение треугольников. Вот код.

Всё просто: как и раньше, пробегаем по всем треугольникам, превращаем мировые координаты в экранные и рисуем треугольники. Подробное описание разных систем координат в последущих статьях. Должно получиться нечто вроде этого:

Видео:Треугольник в НейроГрафике. НейроГрафикаСкачать

Плоская тонировка

Давайте теперь убирать эти клоунские цвета и освещать нашу модель.
Капитан Очевидность: «При одной и той же итенсивности света полигон освещён максимально ярко, если свет ему перпендикулярен».

Нулевую освещённость мы получим, если полигон параллелен вектору света.
Перефразируем: интенсивность освещённости равна скалярному произведению вектора света и нормали к данному треугольнику.
Нормаль к треугольнику может быть посчитана просто как векторное произведение двух его рёбер.

Но ведь скалярное произведение может быть отрицательным, что это означает? Это означает, что свет падает позади полигона. Если модель хорошая (обычно не наша забота, а 3д моделеров), то мы просто можем этот треугольник не рисовать. Это позволяет быстро убрать часть невидимых треугольников. В англоязычной литературе называется Back-face culling.

Модель моей головы выглядит детальнее? Ну так в ней четверть миллиона треугольников. Ничего, детали мы добавим позже, получив картинку, которую я дал для затравки в первой статье.

Обратите внимание, внутренняя полость рта нарисовалась поверх губ. Ну а что, такое быстрое отсечение невидимых треугольников убирает всё ненужное только для выпуклых моделей. Эти огрехи мы уберём в следующий раз, закодировав z-buffer.

Видео:Нейрографика: работа с треугольниками, алгоритм "Прорыв"Скачать

Алгоритм для рисования треугольника

Друзья

Растеризация треугольника. Алгоритм заливки (заполнения)

Одним из важнейших алгоритмов растеризации является алгоритм растеризации треугольника (заполнения треугольника), т.к. в большинстве моделей построения трехмерных объектов последние состоят именно из треугольников.

Прим. В некоторых статьях этот алгоритм называется алгоритм рисования треугольника.

Схематично алгоритм можно описать следующим образом:

Треугольник разбивается на две части вертикальной линией, проходящей через среднюю точку:

Каждый из двух полученных треугольников растеризуется по отдельности.
В процессе растеризации обе стороны растеризуются параллельно, таким образом, чтобы координаты по оси y текущих точек на обоих отрезках совпадали. При этом связность растеризуемых линий (сторон треугольника) не обеспечивается:

При получении координат текущих точек горизонтальныйотрезок между ними заполняется.

При растеризации отрезков сторон используется один из алгоритмов рассмотренных ранее. Т.к. связность отрезков не обеспечивается в силу того, что единичное приращение всегда идет по оси y , будем использовать алгоритм DDA-линии с фиксированной точкой.

Приведем код алгоритма и дадим некоторые комментарии по его работе.

В функцию растеризации передаются три вершины треугольника и дескриптор контекста устройства * .

#include #include «math.h» #include «fixed.h» #define roundf(x) floor(x + 0.5f ) inline void swap( int &a, int &b) < int t; t = a; a = b; b = t; >
void triangle(HDC hdc, int x1, int y1, int x2, int y2, int x3, int y3) <
// Упорядочиваем точки p 1( x 1, y 1), // p2(x2, y2), p3(x3, y3) if (y2 swap(y1, y2); swap ( x 1, x 2); > // точки p 1, p 2 упорядочены if (y3 swap(y1, y3); swap ( x 1, x 3); > // точки p 1, p 3 упорядочены // теперь p 1 самая верхняя // осталось упорядочить p 2 и p 3 if (y2 > y3) < swap(y2, y3); swap ( x 2, x 3); >
// приращения по оси x для трёх сторон // треугольника fixed dx 13 = 0, dx 12 = 0, dx 23 = 0; // вычисляем приращения // в случае, если ординаты двух точек // совпадают, приращения // полагаются равными нулю if ( y 3 != y 1) < dx13 = int_to_fixed(x3 — x1); dx13 /= y3 — y1; > else < dx13 = 0; > if (y2 != y1) < dx12 = int_to_fixed(x2 — x1); dx12 /= (y2 — y1); > else < dx12 = 0; > if (y3 != y2) < dx23 = int_to_fixed(x3 — x2); dx23 /= (y3 — y2); > else < dx23 = 0; >	Вычисляем приращения по оси x для трёх сторон треугольника. Если ординаты двух точек совпадают (отсутствует верхний, нижний или оба полутреугольника), приращения полагаются равными нулю ** .
// «рабочие точки» // изначально они находятся в верхней точке fixed wx1 = int_to_fixed(x1); fixed wx 2 = wx 1;
// сохраняем приращение dx 13 в другой переменной int _ dx 13 = dx 13; // упорядочиваем приращения таким образом, чтобы // в процессе работы алгоритмы // точка wx 1 была всегда левее wx 2 if ( dx 13 > dx 12) < swap ( dx 13, dx 12); >	Упорядочиваем приращения таким образом, чтобы в процессе работы алгоритмы точка wx1 была всегда левее wx2 . При этом приращение dx13 может быть потеряно, оно заранее сохраняется в переменной _ dx13 .
// растеризуем верхний полутреугольник for ( int i = y 1; i y 2; i ++) < // рисуем горизонтальную линию между рабочими // точками for ( int j = fixed_to_int(wx1); j j++) < SetPixel(hdc, j, i, 0); > wx1 += dx13; wx 2 += dx 12; > Важно! Обратите внимание на граничные условия цикла. Средняя точка с ординатой y2 здесь не рисуется. При у1 = y2 (отсутствует верхний полутреугольник) на этом шаге ничего выведено не будет.
// вырожденный случай, когда верхнего полутреугольника нет // надо разнести рабочие точки по оси x, т.к. изначально они совпадают if ( y 1 == y 2) < wx1 = int_to_fixed(x1); wx2 = int_to_fixed(x2); >
// упорядочиваем приращения // (используем сохраненное приращение) if (_dx13 < swap(_dx13, dx23); >	Упорядочиваем приращения таким образом, чтобы в процессе работы алгоритмы точка wx1 была всегда левее wx2 . При этом используется сохраненное приращение _dx13 .
// растеризуем нижний полутреугольник for ( int i = y2; i // рисуем горизонтальную линию между рабочими // точками for ( int j = fixed_to_int(wx1); j SetPixel(hdc, j, i, 0); > wx1 += _dx13; wx2 += dx23; > >

Прим. * В следующей статье будет рассказано, как выводить изображение в память.
** Если внимательно проанализировать алгоритм, становится видно, что в вырожденных случаях, при y 1 = y 2 , y 2 = y 3 или y 1 = y 3 на соответствующих шагах алгоритма приращения dx 12, dx 23 или dx 13 использованы не будут. Поэтому их можно не приравнивать нулю в этих случаях :

if (y3 != y1) <
dx13 = int_to_fixed(x3 — x1);
dx13 /= y3 — y1;
>
~~else~~

Прим. Приведенная реализация может быть улучшена при помощи использования различных ухищрений, ассемблерных вставок и т.д. Настоящая статья ставит своей целью раскрыть принципиальное содержание алгоритма, сохраняя в коде разумное соотношение между простотой понимания и эффективностью работы.

Слабым местом в приведенной реализации является вывод пикселей на экран. Использование функции SetPixel в данном случае крайне неразумно. Вывод в память на порядок увеличит скорость работы приложения и избавит от необходимости реализовывать двойную буферизацию через теневой контекст устройства.

Скачать исходные тексты демонстрационных программ (в программе, при нажатии на любую клавишу, можно посмотреть, как отрисует тот же треугольник стандартная WinAPI функция)

Видео:Что скрывает фрактальный треугольник? // Vital MathСкачать

Программирование на C, C# и Java

Видео:Треугольник в нейрографикеСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:Сколько треугольников на рисунке? Универсальный алгоритм решения задачиСкачать

Растеризация треугольников на основе барицентрических координат C#

В этой статье мы рассмотрим алгоритм и пример программы, растеризующей треугольники с интерполяцией атрибутов вершин на основе барицентрических координат. Звучит громоздко? Не пугайтесь, все не настолько сложно.

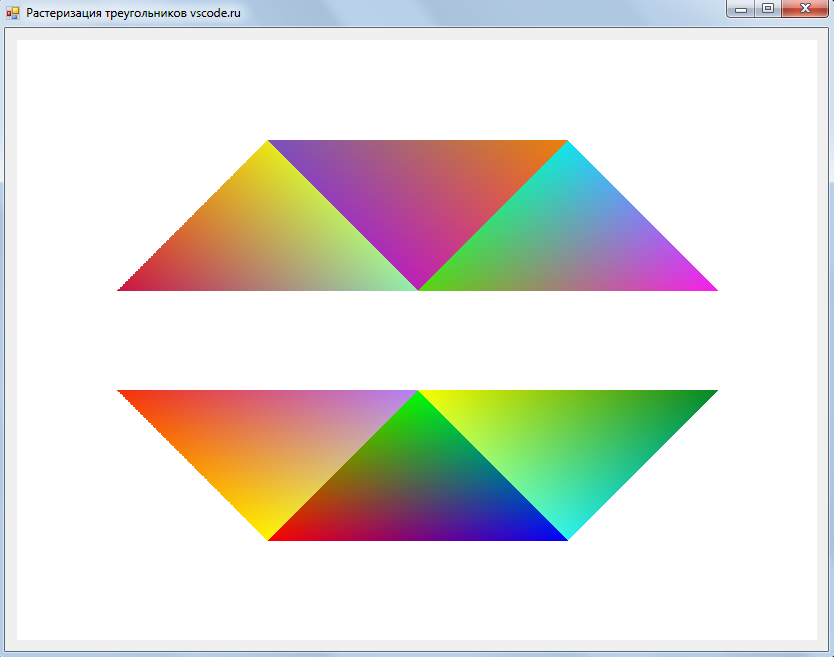
В результате разработки, мы получим программу, которая будет рисовать на экране вот такое изображение:

Итак, обо всем по порядку.

Допустим у нас имеется шесть треугольников. Даны их координаты и заданы атрибуты их вершин (цвета в вершинах). Необходимо растеризовать с интерполяцией атрибутов вершин (или проще – раскрасить, зная цвета вершин) эти треугольники. Получим своеобразный градиент.

Примечание. Интерполяция – это получение промежуточных значений величины, на основе набора известных значений.

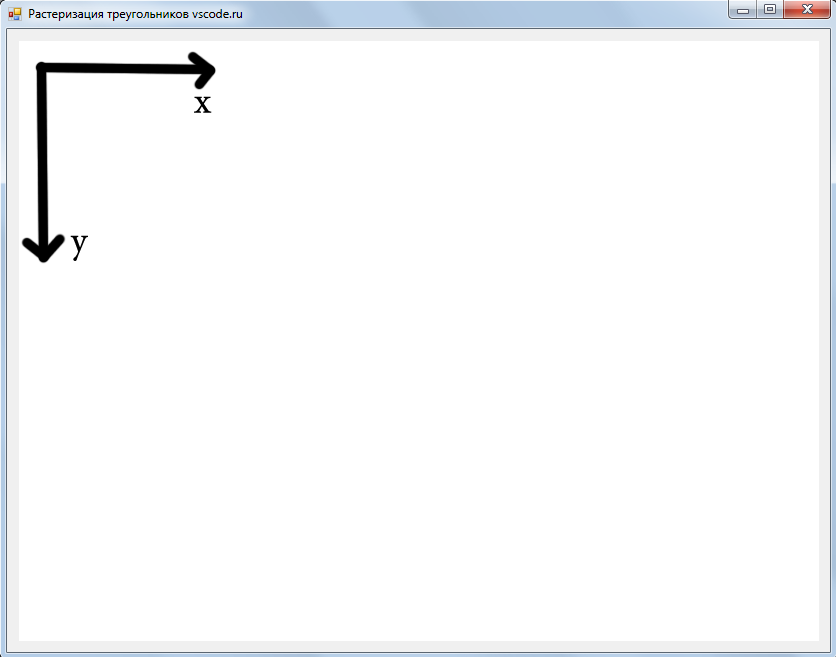
Допустим, у нас имеется pictureBox размером 800 x 600 пикселей. За начало координат примем левый верхний угол.

В цикле for будем перемещаться по координатной плоскости (по пикселям) построчно – слева направо. Наша задача состоит в том, что бы определить, принадлежат ли координаты текущего пикселя какому-либо из треугольников. Для решения этой задачи нам потребуется использовать барицентрические координаты. Вот их формулы:

где x1, y1, x2, y2, x3, y3 – координаты вершин треугольника, а x, y – координаты текущей точки. Текущая точка принадлежит треугольнику, если выполняется условие:

(то есть все три барицентрические координаты должны принадлежать отрезку [0, 1])

Подробнее прочитать про барицентрические координаты можно здесь и здесь.

В итоге имеем такой алгоритм растеризации треугольника:

1) Значению цвета текущей точки присваивается цвет фона.

2) Вычисляются барицентрические координаты текущей точки относительно вершин текущего треугольника.

3) Выполняется проверка условия принадлежности точки треугольнику.

4) Если условие верно, то точка принадлежит треугольнику, и значению ее цвета присваивается цвет, полученный при интерполяции атрибутов вершин этого треугольника. Иначе: переходим к следующему треугольнику (если такой [еще] имеется) и пункту 2.

5) Вывод текущей точки, переход к следующей и пункту 1.

Итак, создадим в Visual Studio проект Windows Forms (С#). Поместим в форму элемент управления pictureBox и зададим в свойствах его размеры 800 x 600: