Нормаль вектор и линии уровня

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

Видео:Математика без Ху!ни. Функции нескольких переменных. Область определения. Линии уровня.Скачать

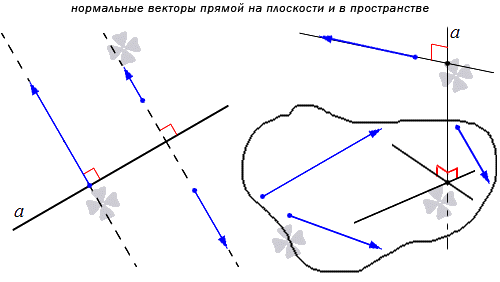
Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.

Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .

Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .

Видео:Поверхности и линии уровняСкачать

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой

При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Задана прямая вида 2 x + 7 y — 4 = 0 _, найти координаты нормального вектора.

По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .

Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.

Указать нормальный вектор для заданной прямой y — 3 = 0 .

По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y — 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .

Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.

Найти координаты нормального вектора, если дано уравнение прямой x 1 3 — y = 1 .

Для начала необходимо перейти от уравнения в отрезках x 1 3 — y = 1 к уравнению общего вида. Тогда получим, что x 1 3 — y = 1 ⇔ 3 · x — 1 · y — 1 = 0 .

Отсюда видно, что координаты нормального вектора имеют значение 3 , — 1 .

Ответ: 3 , — 1 .

Если прямая определена каноническим уравнением прямой на плоскости x — x 1 a x = y — y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .

Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0

Для решения можно выбирать любой удобный способ.

Найти нормальный вектор заданной прямой x — 2 7 = y + 3 — 2 .

Из прямой x — 2 7 = y + 3 — 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , — 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , — 2 ) .

Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , — 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x — 2 · n y = 0 .

Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 — 2 · n y = 0 ⇔ n y = 7 2 .

Значит, нормальный вектор имеет координаты 1 , 7 2 .

Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем

x — 2 7 = y + 3 — 2 ⇔ 7 · ( y + 3 ) = — 2 · ( x — 2 ) ⇔ 2 x + 7 y — 4 + 7 3 = 0

Полученный результат координат нормального вектора равен 2 , 7 .

Ответ: 2 , 7 или 1 , 7 2 .

Указать координаты нормального вектора прямой x = 1 y = 2 — 3 · λ .

Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:

x = 1 y = 2 — 3 · λ ⇔ x = 1 + 0 · λ y = 2 — 3 · λ ⇔ λ = x — 1 0 λ = y — 2 — 3 ⇔ x — 1 0 = y — 2 — 3 ⇔ ⇔ — 3 · ( x — 1 ) = 0 · ( y — 2 ) ⇔ — 3 · x + 0 · y + 3 = 0

Отсюда видно, что координаты нормального вектора равны — 3 , 0 .

Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .

Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .

Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Нормали и обратное транспонирование, часть 2: сопряжённые пространства

В первой части мы рассмотрели внешнюю алгебру и поняли, что векторы нормали в 3D можно интерпретировать как бивекторы. Для преобразования бивекторов в общем случае нужна матрица отличная от той, которая преобразует обычные векторы. Воспользовавшись каноническим базисом для бивекторов, мы выяснили, что это присоединённая матрица, которая пропорциональна обратной транспонированной. Эти рассуждения хотя бы частично объяснили почему нормали преобразуются обратной транспонированной матрицей.

Но некоторые вопросы были заметены под ковёр.

Мы рассмотрели присоединённые матрицы, но не показали как они связаны с алгебраическим доказательством того, что для преобразования уравнения плоскости нужна обратная транспонированная матрица. Пропорциональность между матрицами была в некотором смысле притянута за уши.

Более того, мы увидели, что -векторы из внешней алгебры снабжают векторные геометрические объекты естественной интерпретацией, в которой они содержат единицы длины, площади и объёма, измкеняющиеся соответствующим образом при масштабировании. Но мы не нашли ничего подобного для плотностей — единиц, обратных к длине, площади и объёму.

В этой статье мы рассмотрим ещё одну геометрическую концепцию, которая понадобится для завершения картины. Слияние этой новой концепции с уже изученной внешней алгеброй прояснит и разрешит оставшиеся вопросы.

Видео:Направляющий и нормальный вектор прямой на плоскости | Векторная алгебраСкачать

Функции как векторы

Большая часть этой статьи будет рассматривать функции, которые принимают и возвращают векторы различных типов. Чтобы её понять, нужно совершить некоторый умственный кувырок, который может показаться контринтуитивным, если вы не встречали его ранее.

Вот он: функции, которые возвращают векторы, сами являются векторами

С первого взгляда это утверждение может показаться бессмысленным. Векторы и функции — это совершенно разные вещи, как например яблоки и… стулья, не так ли? Как функция буквально может быть вектором?

Посмотрев на формальное определение векторного пространства, вы не найдёте в нем ничего конкретного о структуре векторов. Мы часто представляем их себе как стрелки с длиной и направлением, или как упорядоченные наборы чисел (координат). Но всё же, в сухом остатке для создания векторного пространства нужен набор сущностей, которые поддерживают две базовые операции: сложение между собой и умножение на скаляры (здесь это действительные числа). Эти операции должны подчиняться нескольким разумным аксиомам.

Функции тоже можно складывать между собой! Две функции и можно сложить поточечно и получить новую функцию для каждой точки в области определения. Аналогично, функция может быть поточечно умножена на скаляр: . Эти операции удовлетворяют аксиомам векторного пространства, потому любое множество подходящих функций формирует полноправное векторное пространство, называемое функциональным пространством.

Запишем формальнее: пусть есть область определения (любое множество, не обязательно векторное пространство) и область значений — векторное пространство. Тогда множество функций образуют векторное пространство относительно поточечного сложения и умножения на скаляр. Область значений должна быть векторным пространством чтобы в нём работало сложение и перемножение значений функции, но области определения не обязательно быть векторным пространством, и вообще «пространством». Она может быть хоть дискретным множеством.

Понимание трактовки функций как векторов даёт возможность применять методы линейной алгебры при работе в функциями. Получается большая ветвь математики, называемая функциональным анализом.

Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Линейные формы и сопряжённое пространство

Отсюда и далее будем рассматривать особый класс функций, называемый линейными формами.

Пусть есть векторное пространство , например трёхмерное , тогда линейная форма на определяется как линейная функция . То есть, это линейная функция которая принимает вектор и возвращает скаляр.

(Замечание для математиков: в этой статье я рассматриваю только конечномерные пространства над , поэтому некоторые утверждения могут быть неверны для векторных пространств в общем случае. Извините!)

Мне нравится визуализировать линейные формы как последовательности параллельных равноотстоящих плоскостей (3D) или линий (2D), то есть линий/поверхностей уровня функции, отстоящих друг от друга на единицу в величинах значений функции. Вот несколько примеров:

Здесь градиенты показывают ориентацию линейной формы — функция возрастает в сторону возрастания непрозрачности градиента. Линии резкого изменения цвета пересекают оси в целых точках. Заметим, что «бо́льшие» линейные формы (в смысле бо́льших выходных значений) соответствуют более плотному размещению линий, и наоборот.

Выше показано, что линейные формы над векторным пространством могут сами трактоваться как векторы в своём собственном функциональном пространстве. Линейные комбинации линейных функций так же являются линейными функциями, потому они образуют полноценное векторное пространство.

Это линейное пространство — множество линейных форм над — достаточно значимо, чтобы иметь отдельное название: сопряжённое (или двойственное) пространство. Оно обозначается через . Элементы двойственного пространства (линейные формы) называются двойственными векторами или ковекторами.

Естественная свёртка

Тот факт, что двойственные векторы — это линейные, а не какие угодно функции из в , сильно ограничивает их поведение. У линейных функций на -мерном векторном пространстве есть только степеней свободы, в отличие от произвольных функций, у которых может быть сколько угодно степеней свободы. Иными словами, у та же размерность, что и у .

Конкретнее, линейная форма на полностью определяется своими значениями при применении к векторам базиса. Значение на любом другом векторе может быть выведено через линейность. Например, если — линейная форма над и — произвольный вектор, то:

Если вы думаете, что это выражение выглядит очень похожим на скалярное произведение и — вы правы!

Действительно, операция применения линейной формы к вектору имеет свойства произведения между сопряжённым пространством и основным: . Это произведение называется естественной свёрткой.

Как и скалярное произведение векторов, естественная свёртка возвращает действительное число, и является билинейной, то есть линейной по обоим аргументам. Тем не менее, здесь мы берём произведение не двух векторов, а двойственного вектора с «обычным» вектором. Линейность по левому аргументу получается из поточечного сложения и умножения линейных форм, а по правому — из того, что линейные формы… линейны на своих векторных аргументах.

Далее будем обозначать естественную свёртку угловыми скобками: . Здесь — двойственный вектор в , а — вектор в . Повторюсь, что это лишь вычисление линейной формы как функции от вектора . Но так как функции это векторы, а двойственные векторы — линейные функции, эта операция имеет свойства произведения.

Вышеприведённая формула выглядит вот так в новой нотации с угловыми скобками:

Обратите внимание, что теперь эта операция выглядит «всего лишь» как навешивание дистрибутивного атрибута, чем она и является.

Двойственный базис

Вышеупомянутую конструкцию можно использовать для определения канонического базиса для данного базиса . Конкретнее, нам нужно сделать числа координатами ковектора в некотором базисе, так же как являются координатами в базисе пространства . Этого можно достичь определением двойственных базисных векторов при условиях:

и аналогичных для . Все девять условий можно записать кратко:

Этот двойственный базис существует и единственный для заданного базиса в .

Геометрически, двойственный базис состоит из линейных форм, которые отмеряют расстояние вдоль каждой из осей, а поверхности уровня этих линейных форм параллельны всем остальным осям. Они не обязаны быть перпендикулярными оси, которую отмеряют. Это происходит, только если базис ортонормированный. Это свойство сыграет важную роль ниже.

Вот пара примеров векторных базисов и соответствующих им двойственных базисов:

А вот пример разложенной по базису линейной формы :

Возьмём двойственный базис из определения выше и выразим двойственный вектор и вектор через соответствующие базисы. Тогда естественная свёртка скукоживается до скалярного произведения:

Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Преобразования двойственных векторов

В предыдущей статье мы видели, что хотя векторы и бивекторы кажутся структурно одинаковыми (у обоих по три компоненты в трёхмерном случае), они имеют различный геометрический смысл и поведение при преобразованиях, в частности, при масштабировании.

Двойственные векторы становятся третьим примером в этом классе объектов! Двойственные векторы тоже «вектороподобны» (подчиняются аксиомам векторного пространства), структурно схожи с векторами и бивекторами (состоят из трёх компонент в 3D), но имеют другой геометрический смысл (линейные формы). Так давайте же посмотрим на поведение двойственных векторов при трансформациях!

Двойственные векторы — это линейные формы, то есть функции. Как преобразовать функцию?

Можно вообразить это так: значения функций идут вместе с аргументами из области определения. Вообразите, что каждая точка в области определения помечена значением функции. Применим преобразование к точкам: они куда-то передвинутся и перенесут с собой свои метки. (А ещё это можно вообразить как преобразование графика функции, понимаемого как набор точек в пространстве на размерность выше).

Более формально: пусть на векторы действует матрица , и эту же матрицу нужно применить к функции , чтобы получилась новая функция . Для этого нужно лишь чтобы от преобразованного вектора равнялась от исходного вектора:

Иными словами, функцию можно преобразовать, соорудив новую функцию которая применяет обратное преобразование к своему аргументу и подаёт его в исходную функцию.

Заметим, что это работает только для обратимых . В противном случае наша картинка про «перенос значений функции вместе с аргументами» рассыпается: необратимая может схлопнуть несколько различных точек области определения в одну.

Однородное масштабирование

Теперь, когда мы понимаем как преобразовать функцию, давайте посмотрим на однородное масштабирование. Возьмём коэффициент 0$» data-tex=»inline»/>, тогда вектор будет отображаться как . Тогда функции будут преобразованы как согласно предыдущему разделу.

Давайте теперь посмотрим на это с точки зрения двойственного вектора, а не функции. Если для некоторого вектора , то что произойдёт при масштабировании в раз?

Я всего лишь переместил множитель с одной стороны угловых скобок на другую, что допустимо, так как угловые скобки билинейны. Итак, мы показали что двойственный вектор преобразуется следующим образом:

Это интересно! При масштабировании вектора в раз, двойственный вектор масштабируется как . В предыдущей статье мы оправдали назначение единиц «площади» и «объёма» бивекторам и тривекторам через их поведение при масштабировании. Следуя этому принципу заключим, что двойственные векторы несут единицы, обратные длине!

Фактически, двойственные векторы представляют ориентированные линейные плотности. Они предоставляют инструментарий для количественных рассуждений о ситуациях, когда нечто скалярное (например, количество текселей, прозрачность, изменение электрического напряжения/температуры/давления) распределено вдоль какого-то измерения в пространстве. При свёртывании двойственного вектора с вектором (то есть при вычислении линейной формы над вектором), вы по сути спрашиваете «какое количество этого «нечто» данный вектор охватывает?»

При масштабировании мы сохраняем количество «нечто». Если масштабирование увеличивает, плотность уменьшается, потому что одинаковое количество чего-либо теперь распределяется на большее расстояние, и наоборот. Это свойство воплощается в обратности масштабирования двойственных векторов.

Сдвинутый двойственный вектор и обратное транспонирование

Мы рассмотрели как однородное масштабирование обращается при применении к двойственным векторам. Теперь мы могли бы изучить неоднородное масштабирование, но так получается, что оно не очень интересно — как вы и могли подумать, оно всего лишь применяется как масштабирование на обратную величину к каждой из осей. Куда более показательным будет изучение сдвига.

Для этого нам будет достаточно двумерного случая. Для примера возьмём преобразование, которое немного наклоняет ось в сторону :

Вот как это выглядит:

А что произойдёт если применить это преобразование к двойственному вектору? Визуально всё понятно: изолинии линейной формы наклонятся вслед за сдвигом.

Но как это выразить в виде матрицы, действующий на координаты двойственного вектора? Давайте присмотримся к компоненте . Заметим, что преобразование не повлияло на ось — она отобразилась сама в себя. Но что насчёт ?

Компонента изменяется этим преобразованием, потому что изолинии приобретают наклон! Иными словами, несмотря на то, что расстояния вдоль оси не изменились, «отслеживает» что делают другие оси, потому что ей надо оставаться параллельной этим осям. Это одно из определяющих условий, на которых работает двойственный базис.

Строго говоря, здесь переходит в . Доводя дело до конца, мы увидим, что вся матрица, применяемая к координатам двойственного вектора, имеет вид

А это и есть обратная транспонированная !

Прослеживается некоторая аналогия эффекта обратной транспонированной матрицы, рассмотренной здесь, с воздействием присоединённой матрицы на бивекторы из предыдущей статьи. Как и с бивекторами, каждый элемент двойственного базиса следит за тем, что происходит с другими осями (чтобы сохранять параллельность им), но так же масштабируется на обратную величину вдоль своей оси. Определитель соответствует совокупному масштабированию по всем осям:

Отсюда мы можем перейти к

что соответствует соотношению между обратной транспонированной и присоединённой матрицами.

Здесь я проделываю очень нестрогий трюк, потому что хорошая геометрическая демонстрация заведёт нас в ещё большие дебри, а такой способ даёт хоть немного интуитивного понимания почему обратную транспонированную матрицу правомерно применять к двойственным векторам.

Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Так что же такое вектор нормали?

Ранее мы увидели, что поверхности уровня линейной формы — это параллельные линии в 2D или плоскости в 3D. Отсюда следует, что мы можем определить плоскость, взяв определённую поверхность уровня данного двойственного вектора:

Двойственный вектор выступает как знаковое поле расстояний плоскости.

Так же мы увидели, что если выразить естественную свёртку в терминах базиса и соответствующего ему двойственного базиса, то она превратится в скалярное произведение . После чего уравнение выше становится обычным уравнением плоскости:

Отсюда видно, что координаты двойственного вектора в двойственном базисе так же являются координатами вектора нормали в стандартном векторном базисе.

Итак, векторы нормали можно интерпретировать как двойственные векторы в двойственном базисе, поэтому они преобразуются обратной транспонированной матрицей.

Но постойте. В предыдущей статье я сказал, что нормали надо понимать как бивекторы, а потому их надо трансформировать присоединённой матрицей, не так ли? Как правильно то?

Мне кажется, на этот вопрос нет единственного правильного ответа. Идея «нормального вектора» слишком расплывчата, и её можно оправдано формализовать как через бивекторы, так и через двойственные векторы. Как было показано, оба способа преобразования эквивалентны в смысле ориентации: и бивекторы и двойственные векторы остаются перпендикулярными определяющей их плоскости, следуя условиям или соответственно. Различаются они только единицами измерения и реакцией на масштабирование: бивекторы это площади и объёмы, а двойственные векторы — это обратные длины.

Это всё что я хотел рассказать о преобразованиях нормальных векторов, но ещё несколько вопросов остались в подвешенном состоянии. В конце первой части я задавал вопрос об отрицательных степенях масштаба. Теперь у нас есть минус первая степень, но что насчёт -2 и -3? Чтобы это понять, нам придётся скомбинировать внешнюю алгебру и двойственные пространства, чем мы и займёмся в третьей части.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Линии и поверхности уровня

Содержание:

Видео:Линии уровня и поверхности уровня функции многих переменныхСкачать

Линии и поверхности уровня

Понятие линии и поверхности уровня:

Для характеристики функций двух переменных вводится понятие линий уровня.

Определение 2. Линией уровня функции z = f (x, y) называется совокупность всех точек на плоскости Oxy, для которых выполняется условие f (x, y) = C.

Линии уровня можно получить, пересекая поверхность z = f (x, y) плоскостями z = C, где С = соnst.

Пример 1. Найти линии уровня функции z = x 2 + y 2 .

Решение.
Пусть z = C. x 2 + y 2 = C (C ≥ 0),

В этом случае линиями уровня является множество концентрических окружностей с центром в начале координат и радиусом С (рис. 2) .Аналогично вводится понятие поверхности уровня для функции трех переменных u = f (x, y, z), (f (x, y, z) = C).

Пример 2. Найти поверхности уровня функции u = x 2 + y 2 + z 2 .

Решение. Пусть u = C. Тогда x 2 + y 2 + z 2 = C (C ≥ 0) — это множество сфер с центром в точке O(0; 0; 0) и радиусом C.

Поверхности второго порядка

Наиболее изучены поверхности в курсе аналитической геометрии — поверхности второго порядка. В общем случае уравнение такой поверхности имеет вид:
a₁₁ x 2 + 2a₁₂ xy + a₂₂ y 2 + 2a₁₃ xz + 2a₂₃ yz + a₃₃ z 2 + 2a₁₄ x + 2a₂₄ y + 2a₃₄ z + a₄₄ = 0.

В зависимости от значений коэффициентов получают различные поверхности второго порядка.

Например:
1) — конус;

2) — полусфера;

Рис. 4.

3) — эллиптический параболоид;

Рис. 5.

4) — гиперболический параболоид;

рис.6

5) — трехосный эллипсоид.

Рис. 7.

Для изучения поверхностей в трехмерном пространстве применяется метод сечений. Суть этого метода такова: пересекаем заданную поверхность плоскостями x = C₁, y = C₂, z = C₃. В результате получим некоторые кривые, характеризующие поверхность.

Пример 3. z = x 2 + y 2 . Пусть z = C₁ (C₁ ≥ 0). Получим уравнение x 2 + y 2 = C₁ (уравнение окружности). Положим y = C₂ , тогда — уравнение параболы в плоскости Оxz, которая смещена на единиц вверх по оси Oz. Положим x = C₃ , получим уравнение
Получили уравнение параболы в плоскости Оyz, которая смещена на единиц вверх по оси Оz. Из этих исследований вытекает, что графиком функции z = x 2 + y 2 является параболоид вращения вокруг оси Оz.

Видео:Репетитор по математике ищет нормаль к плоскостиСкачать

Гиперповерхности уровня

Пусть задана функция от n переменных u = f (x₁, x₂, . x_n) . Если положить u = C, то получим уравнение f (x₁, x₂, . x_n) = C, которое называется уравнением гиперповерхности уровня в пространстве R n . Например: Если u = C, то уравнение является уравнением гиперсферы в R n с центром в точке O (0,0, . 0) и радиусом .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

🎬 Видео

Уравнения прямой на плоскости | Векторная алгебраСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

10. ФНП. Градиент и производная по направлению функции двух переменных.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

2. Область определения функции двух переменныхСкачать

2017. Градиент скалярной функции векторного аргумента. Линии уровня.Скачать

11. Прямая в пространстве и ее уравненияСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Уравнения касательной плоскости и нормали к поверхностиСкачать