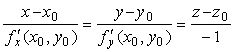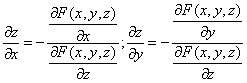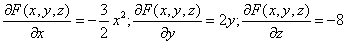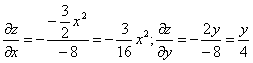Нормаль поверхности параллельна вектору

Обозначения:
— $vec=$ — радиус-вектор произвольной точки касательной плоскости.
— $vec=$ — радиус вектор точки $P(u_0, v_0)$.
— Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.

Уравнение касательной плоскости:

1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end

Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.

Уравнение нормали:

1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac=displaystylefrac=displaystylefrac. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac. end

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Решение задач

Задача 1 (Феденко №574)

Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefracright)$ поверхности.

Задача 2

Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.

Ответ. $z=0, -2X-2Y+Z+2=0$.

Задача 3

Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec$.

Задача 4

Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.

Ответ. $X-Z=0$, $3X-4Y+5Z=0$.

Задача 5 (Феденко №594)

Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.

Решение задачи 5

Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Видео:Касательная плоскость и нормаль к поверхностиСкачать

Поверхности

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Простые поверхности.

Будем говорить, что функция (f(u, v)) непрерывно дифференцируема на замкнутом множестве (E subset boldsymbol^), если она определена и имеет непрерывные частные производные (partial f/partial u) и (partial f/partial v) на открытом множестве (G), содержащем замкнутое множество (E).

Пусть (Omega) — ограниченная область в (boldsymbol^), а функции (varphi(u, v)), (psi(u, v)) и (chi(u, v)) непрерывно дифференцируемы на замкнутом множестве (overline = Omega cup partial Omega), где (partial Omega) — граница области (Omega). Тогда отображение (F: overline rightarrow boldsymbol^), определяемое формулами
$$
x = varphi(u, v),quad y = psi(u, v),quad z = chi(u, v),quad (u, v) in overline,label
$$
называется непрерывно дифференцируемым.

Если при этом в каждой точке ((u, v) in Omega) ранг функциональной матрицы
$$
beginvarphi_(u, v)&psi_(u, v)&chi_(u, v)\varphi_(u, v)&psi_(u, v)&chi_(u, v)endlabel
$$
равен двум, то отображение (F: rightarrow boldsymbol^) называется гладким.

Если (overline) есть замкнутое ограниченное множество в (boldsymbol^), a (F: overline rightarrow boldsymbol^) есть такое гладкое отображение, что соответствие между множествами (overline) и (Sigma = F(overline)) является взаимно однозначным, то будем множество (Sigma) называть простой поверхностью в (boldsymbol^), а уравнения eqref будем называть параметрическими уравнениями простой поверхности (Sigma).

Пусть область (Omega) ограничена простым гладким или кусочно гладким контуром (gamma). Образ кривой (gamma) при гладком отображении (F: overline rightarrow boldsymbol^) будем называть краем простой поверхности (Sigma) и обозначать через (partial Sigma).

Если уравнение кривой (gamma) имеет вид
$$
u = u(t),quad v = v(t),quad alpha leq t leq beta,nonumber
$$
то уравнение (partialSigma) задается следующими формулами:
$$
x = varphi(u(t), v(t)),quad y = psi(u(t), v(t)),quad z = chi(u(t), v(t)),quad alpha leq t leq beta.label
$$

График функции (z = f(x, y)), непрерывно дифференцируемой на замкнутом ограниченном множестве (overline subset boldsymbol^), есть простая поверхность, определяемая параметрическими уравнениями
$$
x = u,quad y = v,quad z = f(u, v),quad (u, v) in overline.label
$$

В этом случае матрица (beginx_&x_\x_&y_end) является единичной, а поэтому ранг матрицы eqref равен двум.

Например, график функции (z = x^ + y^), ((x, y) in overline), где (overline = <(x, y): x^+ y^ leq 1>), есть простая поверхность. Окружность, получаемая при пересечении параболоида вращения (z = x^ + y^) и плоскости (z = 1), является краем рассматриваемой простой поверхности.

Уравнения eqref простой поверхности можно записать и в векторной форме:
$$
boldsymbol = boldsymbol(u, v),quad (u, v) in overline,quad boldsymbol(u, v) = varphi(u, v) boldsymbol + psi(u, v) boldsymbol + chi(u, v) boldsymbol.label
$$

С механической точки зрения формулы eqref определяют гладкую (без разрывов и изломов) деформацию плоской области (Omega) в множество (Sigma) (простую поверхность в пространстве (boldsymbol^)). Для практических целей только простых поверхностей недостаточно. Например, сфера (x^ + y^ + z^ = a^) не является простой поверхностью в (boldsymbol^). Интуитивно ясно, что сферу нельзя получить никакой гладкой деформацией плоской области.

Имея в виду приложения теории поверхностных интегралов, введем в рассмотрение класс почти простых поверхностей.

Пусть (Omega) — плоская область и (F: overline rightarrow boldsymbol^) — непрерывно дифференцируемое отображение. Будем множество (Sigma = F(overline)) называть почти простой поверхностью в (boldsymbol^), если найдется расширяющаяся последовательность ограниченных областей (<Omega_>) таких, что (overline_ subset Omega_), (Omega = displaystylebigcup_^Omega_) и поверхности (Sigma_ = F(overline_)) простые.

Сфера (S = <(x, y, z): x^+ y^ + z^ = a^>) есть почти простая поверхность.

(vartriangle) Введем сферические координаты. Тогда сфера (S) есть образ прямоугольника (overline = displaystyleleft<(varphi, psi): 0 leq varphi leq 2pi, -frac leq psi leq fracright>) при непрерывно дифференцируемом отображении (F: overline rightarrow S), определяемом формулами
$$
x = a cos varphi cos psi,qquad y = a sin varphi cos psi,qquad z = a sin psi.nonumber
$$

Образами отрезков (varphi = varphi_), (displaystyle-frac leq psi leq frac) являются меридианы, а при (displaystyle|psi_| Рис. 52.1

Конус (K = <(x, y, z): x^+ y^ = z^>) есть почти простая поверхность.

(vartriangle) Введем цилиндрические координаты. Тогда конус (K) есть образ полуполосы
$$
overline = <(r, varphi): 0 leq r Рис. 52.2

Легко проверить, что (overline_ subset Omega_), (Omega = displaystylebigcup_^Omega_) и что поверхности (Sigma_ = F(overline_)) являются простыми. Поэтому конус (K) — почти простая поверхность. (blacktriangle)

Если (Sigma) есть простая поверхность, заданная векторным уравнением eqref, а непрерывно дифференцируемые функции
$$
u = u(u’, v’), v = v(u’, v’), (u’, v’) in Omega’nonumber
$$
задают взаимно однозначное отображение замыкания области (Omega’) на замыкание ограниченной области (Omega), причем якобиан отображения
$$
frac = begindisplaystylefrac&displaystylefrac\displaystylefrac&displaystylefracendnonumber
$$
отличен от нуля в (overline’), то уравнение
$$
boldsymbol = boldsymbol (u(u’, v’), v(u’, v’)) equiv boldsymbol(u’, v’);quad (u’, v’) in Omega’,label
$$
определяет ту же простую поверхность, что и уравнение eqref. Уравнения eqref и eqref называют различными параметризациями поверхности (Sigma).

Как и в случае кривых, можно расширить класс параметризаций, допуская и такие замены параметров, при которых непрерывная дифференцируемость, взаимная однозначность и необращение в нуль якобиана отображения нарушаются на границе области. Тогда можно получить такие параметризации простой поверхности, задаваемые функциями, непрерывная дифференцируемость которых не имеет места на границе области (Omega).

(vartriangle) Переход от уравнений eqref к уравнениям eqref задается формулами
$$
u = a cos varphi cos psi,quad v = a sin varphi cos psi,quad (varphi, psi) in Omega’.label
$$

Якобиан отображения eqref равен (a^ sin varphi cos psi) и обращается в нуль при (psi = 0), то есть на части границы области (Omega’). Это приводит к тому, что при переходе к параметризации eqref частные производные функции (z = sqrt<a^-u^-v^>) стремятся к бесконечности при приближении точки (u, v) к окружности (u^ + v^ = a^). (blacktriangle)

Как правило, в дальнейшем для простых поверхностей будут рассматриваться только такие параметризации, которые задаются непрерывно дифференцируемыми на замкнутом ограниченном множестве функциями.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Криволинейные координаты на поверхности.

Пусть простая поверхность (Sigma) задана векторным уравнением eqref. Предположим, что область (Omega) выпукла, ([a, b]) есть проекция области (Omega) на ось (u). Если (u_ = in (a, b)), то прямая (u = u_) будет пересекаться с областью (Omega) по отрезку (u = u_), (alpha leq v leq beta) (рис. 52.3). Образ этого отрезка при отображении eqref есть кривая
$$
boldsymbol = boldsymbol (u_, v), alpha leq v leq beta,label
$$
лежащая на поверхности (Sigma). Будем называть ее координатной кривой (u = u_). Придавая (u_) все значения из отрезка ([a, b]), получим семейство координатных кривых (u = operatorname). Аналогично строится и семейство координатных кривых (v = operatorname).

Рис. 52.3

В силу взаимной однозначности отображения eqref каждая точка (A) поверхности (S) однозначно определяется как пересечение двух координатных кривых, (u = u_) и (v = v_). Пара чисел ((u_, v_)) называется криволинейными координатами точки (A) поверхности. Запись (A(u_, v_)) означает, что точка (A) поверхности (Sigma) задана криволинейными координатами ((u_, v_)).

Например, в сферических координатах часть сферы (x^ + y^ + z^ = a^), ограниченная двумя меридианами и двумя параллелями, задается в криволинейных координатах (varphi), (psi) следующим образом:
$$
varphi_ leq varphi leq varphi_,quad psi_ leq psi leq psi_.nonumber
$$

На сфере координатные кривые (varphi = operatorname) — меридианы, а координатные кривые (psi = operatorname) — параллели.

На прямом круговом цилиндре координатными линиями будут образующие цилиндра и окружности, получающиеся при пересечении цилиндра плоскостями, перпендикулярными образующей.

Вектор-функция (boldsymbol (u_, v)) есть непрерывно дифференцируемая функция параметра (v), и, следовательно, координатная кривая (u = u_), определяемая равенством eqref, является непрерывно дифференцируемой. Вектор (boldsymbol_ (u_, v_)) является касательным к этой кривой в точке (A(u_, v_)). Аналогично, вектор (boldsymbol_ (u_, v_)) касателен к координатной кривой (v = v_) в точке (A(u_, v_)). Заметим, что векторы (boldsymbol_ (u_, v_)) и (boldsymbol_ (u_, v_)) не могут обратиться в нуль, так как в этом случае ранг матрицы eqref будет меньше двух. Следовательно, для простой поверхности координатные кривые являются гладкими.

Если область (Omega) не является выпуклой, а точка ((u_, v_)) лежит внутри (Omega), то нужно взять выпуклую окрестность точки ((u_, v_)), лежащую внутри (Omega). Тогда образ этой выпуклой окрестности будет куском поверхности (Sigma) и координатные кривые можно строить на этом куске поверхности (локально).

Видео:Начертательная геометрия Лекция 9. Касательная плоскость и нормаль к поверхности.Скачать

Касательная плоскость и нормаль к поверхности.

Пусть (Sigma) есть простая поверхность, заданная уравнениями eqref или векторным уравнением eqref. Рассмотрим точку (A(u, v)) на поверхности (Sigma), где ((u, v)) — внутренняя точка области (Omega). Построим координатные линии (u = operatorname) и (v = operatorname), проходящие через точку (A(u, v)). Векторы (boldsymbol_ (u, v)) и (boldsymbol_ (u, v)) будут касательными к соответствующим координатным линиям.

В любой точке (A(u, v)) простой поверхности (Sigma) векторы (boldsymbol_ (u, v)) и (boldsymbol_(u, v)) неколлинеарны. Направление вектора (N = [boldsymbol_, boldsymbol_]) при изменении способа параметризации или не меняется, или изменяется на противоположное.

(circ) Рассмотрим вектор (N = [boldsymbol_, boldsymbol_]) во всех точках поверхности (Sigma). Тогда
$$
boldsymbol=beginy_&z_\y_&z_endboldsymbol + beginz_&x_\z_&x_endboldsymbol + beginx_&y_\x_&y_endboldsymbol.nonumber
$$
Если (boldsymbol = boldsymbol), то все компоненты вектора (boldsymbol) равны нулю, и ранг матрицы eqref будет меньше двух, что невозможно для простой поверхности. Пусть поверхность (Sigma) параметризована двумя способами, eqref и eqref. Тогда, воспользовавшись правилом нахождения частных производных сложной функции и аддитивностью и кососимметричностью векторного произведения, получаем
$$
boldsymbol’ = [boldsymbol_, boldsymbol_] = [boldsymbol_ frac + boldsymbol_ frac, boldsymbol_ frac + boldsymbol_ frac] =\= [boldsymbol_, boldsymbol_] left(fracfrac-fracfracright) = [boldsymbol_, boldsymbol_] frac,nonumber
$$
то есть
$$
boldsymbol’ = boldsymbol frac.label
$$
Так как якобиан (J = displaystylefrac) не обращается в нуль в области (Omega’), то векторы (boldsymbol’) и (boldsymbol) коллинеарны. Эти векторы сонаправлены, если (J > 0), и противоположно направлены, если (J Лемма 2.

Вектор нормали к простой поверхности (Sigma) в точке (A(u_, v_)) ортогонален ко всем гладким кривым, лежащим на поверхности и проходящим через точку (A(u_, v_)).

(circ) В самом деле, такая кривая есть образ при отображении eqref некоторой гладкой кривой, лежащей в области (Omega) и задаваемой уравнениями (u = u(t)), (v = v(t)), (alpha leq t leq beta).

Уравнение кривой на поверхности тогда имеет вид
$$
boldsymbol = boldsymbol(u(t), v(t)), alpha leq t leq beta, u(t_) = u_, v(t_) = v_.
$$

Касательный вектор (boldsymbol) к этой кривой в точке (A) есть
$$
boldsymbol = frac