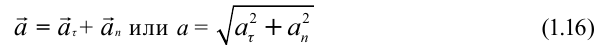Неравномерное движение по окружности ускорение направлено (8 видео)

Неравномерное движение по окружности в физике — формулы и определение с примерами

Неравномерное движение по окружности:

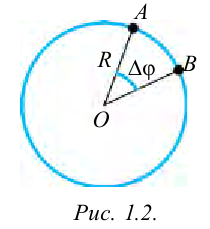
Вы в 7 классе ознакомились с равномерным движением по окружности. В данной теме мы рассмотрим неравномерное движение по окружности. Вспомним физические величины, которые описывают равномерное движение по окружности (рис. 1.2).

Величина, численно равная пути, пройденному за единицу времени равномерно двигающейся по дуге окружности материальной точкой, называется линейной скоростью и определяется следующим выражением:

2. Отношение угла поворота радиуса окружности при равномерном движении по окружности ко времени поворота называется угловой скоростью:

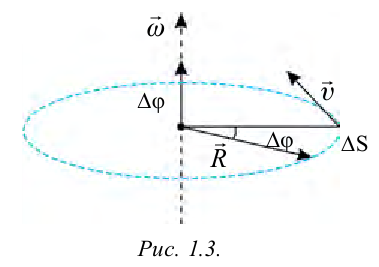
Угловая скорость, также как и линейная скорость, считается векторной величиной. Ее направление определяется по правилу правого винта. То есть, если головку винта вращать по направлению вращения тела, то поступательное движение его укажет направление вектора углового перемещения, или угловой скорости (рис. 1.3).

В большинстве случаев тела, совершающие вращательные движения, меняют скорость вращения. Например, в начале движения автомобиля до достижения им определенной скорости или в момент торможении до полной остановки, колеса автомобиля совершают вращательные движения с разной скоростью.

Движение, при котором угловая скорость предмета, совершающего вращательное движение, изменяется по времени называется переменным вращательным движением.

Среди переменных вращательных движений встречаются движения, в которых угловая скорость за любые равные промежутки времени меняется на равные значения. Например, колеса автобуса, который приближается к остановке или отъезжает от нее, совершают равнопеременное вращательное движение. В таких движениях ритм изменения угловой скорости описывается физической величиной, называемой угловым ускорением.

Величина, измеряемая отношением изменения угловой скорости ко времени, за которое произошло это изменение, называется угловым ускорением.

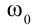
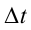
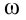
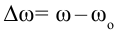
Угловое ускорение при равнопеременном движении с течением времени не меняется, так как угловая скорость такого движения тоже меняется за равные промежутки времени на равные значения. Если начальная угловая скорость двигающейся материальной точки равна , угловая скорость через промежуток времени равна , то изменение угловой скорости будет: . Тогда уравнение (1.12) приобретает вид:

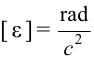
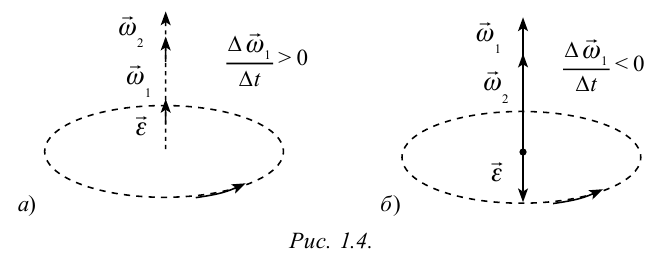
Исходя из этого, единица измерения углового ускорения будет равна . Из выражения (1.13) можно вывести формулу для определения угловой скорости в любой момент времени:

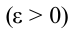
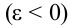
Если угловая скорость в ходе движения растет равномерно, вращательное движение будет равноускоренным (рис. 1.4 а). Если угловая скорость вращательного движения в ходе вращения равномерно уменьшается, такое вращательное движение называется равномерно замедленным (рис. 1.4 б).

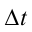
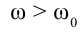
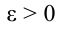
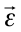
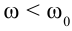
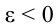
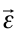
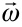
Из-за того, что при вращательном движении угловая скорость является векторной величиной, угловое ускорение тоже считается векторной величиной. Так как, в формуле (1.13) является скалярной величиной. В случае , вектор и угловое ускорение совпадает с направлением угловой скорости, а в случае будет, и вектор противонаправлен вектору .

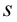
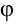
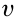
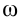
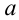
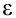
В уравнении равнопеременного прямолинейного движения достаточно заменить пройденный путь на угол поворота , скорость на угловую скорость , ускорение на угловое ускорение чтобы получить уравнение равномерно изменяющегося вращательного движения. Сопоставление этих уравнений для данных видов движения приводится в следующей таблице:

При вращательном движении встречаются случаи, когда меняется количественная величина линейной скорости материальной точки. В таких случаях в связи с изменением линейной скорости материальной точки возникает ускорение. Из-за того, что это ускорение появилось в результате изменения количественных величин скорости, его направление совпадает с направлением скорости. Поэтому оно называется касательным, т.е. тангенциальным ускорением и его можно выразить формулой:

Таким образом, если меняется линейная скорость материальной точки, совершающей вращательное движение, ее общее ускорение можно определить по формуле:

здесь .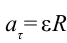

Рекомендую подробно изучить предметы:

Физика
Атомная физика
Ядерная физика
Квантовая физика
Молекулярная физика

Ещё лекции с примерами решения и объяснением:

Равномерное движение по окружности
Взаимная передача вращательного и поступательного движения
Движение горизонтально брошенного тела
Движение тела, брошенного под углом к горизонту
Электромагниты и их применение в физике
Колебательный контур в физике
Исследовательские методы в физике
Вертикальное движение тел в физик

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Содержание

Неравномерное движение по окружности ускорение направлено
Равномерное и неравномерное движение тела по окружности
Движение по окружности
Готовые работы на аналогичную тему
Ускорение равномерного движения по окружности
🔍 Видео

Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Неравномерное движение по окружности ускорение направлено

Выберите все верные утверждения о физических явлениях, величинах и закономерностях.

Запишите в ответе их номера.

1) При неравномерном движении по окружности полное ускорение тела всегда направлено по радиусу к центру окружности.

2) Процесс кристаллизации веществ проходит с выделением большого количества теплоты.

3) Изобарным называется процесс, происходящий с газом неизменной массы при неизменном давлении.

4) В процессе электризации трением два первоначально незаряженных тела приобретают разноимённые, но разные по модулю заряды.

5) Силой Ампера называют силу, с которой магнитное поле действует на проводник с током.

1) Неверно. Полное ускорение при неравномерном движении складывается из нормального и тангенциального ускорения. Нормальное ускорение направлено к центру окружности.

2) Верно. При кристаллизации происходит выделение теплоты.

3) Верно. Изобарный процесс — это процесс, происходящий с газом неизменной массы при постоянном давлении.

4) Неверно. При электризации трением тела приобретают противоположные по знаку и равные по модулю заряды, т. к. происходит перераспределение электронов.

5) Верно. Сила Ампера — это сила, с которой магнитное поле действует на проводник с током.

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Равномерное и неравномерное движение тела по окружности

Вы будете перенаправлены на Автор24

Видео:Физика - движение по окружностиСкачать

Движение по окружности

Частным случаем криволинейного движения в физике является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

Окружность — плоская фигура, поэтому движение по окружности является плоским движением.

Рассмотрим определение движения по окружности.

Равномерное движение по окружности в физике — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.

Положение тела на окружности определяется радиусом-вектором $overrightarrow=R$, проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности: $left|overrightarrowright|=R$.

Рисунок 1. Скорость и перемещение при круговом движении в физике

За время $∆t$ тело, двигаясь из точки $A$ в точку $B$, совершает перемещение $triangle r$, равное хорде $AB$, и проходит путь, равный длине дуги $l$. Радиус-вектор поворачивается на угол $$$$. Угол выражают в радианах.

Скорость $overrightarrow$ движения тела по окружности направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени $triangle t$, за который эта дуга пройдена: $v=frac$

Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется средней угловой скоростью: $omega =frac$. В СИ единицей угловой скорости является радиан в секунду.

Готовые работы на аналогичную тему

При равномерном движении по окружности угловая скорость и модуль линейной скорости величины постоянные: $ = const$; $v = const$.

Положение тела можно определить, если известен модуль радиуса- вектора $overrightarrow$ и угол $$, который он составляет с осью $Ox$ (угловая координата). Если в начальный момент времени $t_0=0$ угловая координата равна $varphi $0, а в момент времени t она равна $varphi $, то угол поворота $∆$$varphi $ радиуса-вектора за время $∆t=t-t_0$ равен $∆$$varphi $=$varphi $-$varphi $0. Тогда из последней формулы можно получить закон равномерного движения материальной точки по окружности:

$varphi = varphi_0 +omega t$

Он позволяет определить положение тела в любой момент времени $t$.

Учитывая, что $triangle varphi =frac$, получаем формулу связи между линейной и угловой скоростью: $omega =frac=frac$

Видео:🔴 ЕГЭ-2024 по физике. Неравномерное движение по окружностиСкачать

Ускорение равномерного движения по окружности

При движении по окружности, как и при всяком криволинейном движении, ускорение можно представить как сумму нормальной $_n$и тангенциальной $_$составляющих: $overrightarrow=_+_n$

При равномерном движении по окружности линейная скорость постоянна, и тангенциальная составляющая ускорения $_<>$=0. Следовательно, в этом случае $overrightarrow=_n$.

Рисунок 2. Ускорение и скорость при равномерном круговом движении

Важнейшими характеристиками равномерного движения по окружности кроме центростремительного ускорения являются период и частота обращения.

Период обращения, который можно выразить в виде $T=frac=frac$ — это время, за которое тело совершается один оборот.

Частота обращения, что отображается $ nu =frac$ — это величина, численно равная числу оборотов, которые совершены за единицу времени. Измеряется частота в 1/с.

Период и частота – величины, которые взаимно обратны: $nu =frac$

Неравномерное движение по окружности отличается от равномерного только тем, что тангенциальная составляющая ускорения $_<>ne 0$, а линейная скорость $v(t)$ и угловая скорость $(t)$ непостоянны, а являются функциями времени.

Для случая равноускоренного движения по окружности

В угловых координатах для движения по окружности с угловой скоростью $omega left(tright)=frac

$, и угловым ускорением $varepsilon =frac

=frac

$, получаем закон равнопеременного движения по окружности: $varphi left(tright)=_0+omega left(tright)t+varepsilon frac$ , где $omega left(tright)=frac;; varepsilon =frac<a_>$.

Задача.

Материальная точка движется по окружности радиусом 3 м со скоростью 12$pi $ м/с. Чему равна частота обращения?

Решение.

Ответ: Частота обращения составляет 4 оборота за секунду

Задача.

Точка начала двигаться по окружности радиусом 0,6 м с тангенциальным ускорением 0,1 м/с2. Чему равны нормальное и полное ускорения в конце третьей секунды после начала движения? Чему равен угол между векторами полного и нормального ускорений в этот момент?

Решение.

$v=v_0+a_t=0.1times 3=0,3 $ м/с