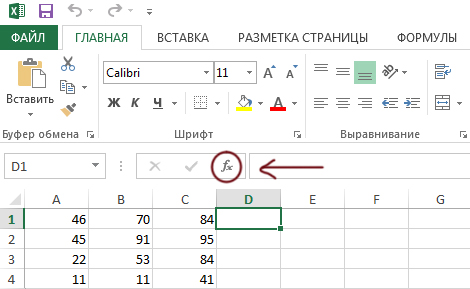
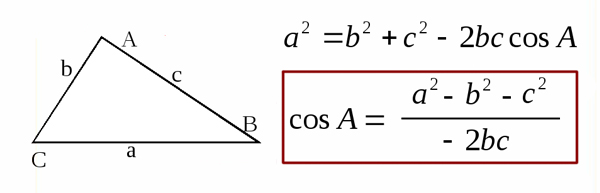Стороны тупоугольного треугольника информатика (8 видео)

Стороны тупоугольного треугольника информатика

Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа.

Определите сколько среди заданных троек чисел таких, которые могут быть сторонами остроугольного треугольника.

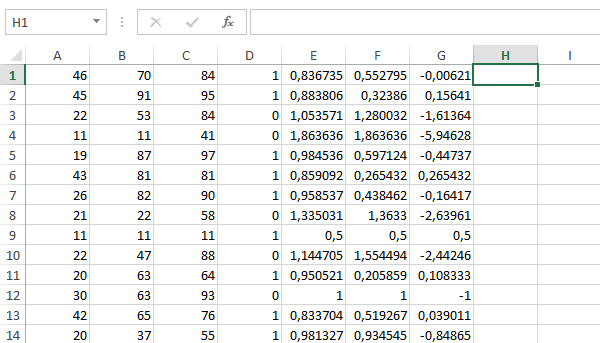
Заметим, что треугольник является остроугольным, если квадрат длины наибольшей стороны треугольника будет меньше суммы квадратов длин других двух сторон. Тогда в ячейке D1 запишем формулу =(МАКС(A1:C1))^2 и скопируем её во все ячейки диапазона D2:D5000. В ячейке E1 запишем формулу

и скопируем её во все ячейки диапазона E2:E5000. Таким образом, получим квадрат длины наибольшей стороны и сумму квадратов других двух сторон для каждой тройки чисел. После этого в ячейку F1 запишем формулу =ЕСЛИ(D1 Ответ: 1074.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

ЕГЭ по информатике 2022 — Задание 9 (Электронная таблица)

Девятое задание из ЕГЭ по информатике 2022 проверяет умение обрабатывать числовую информацию с помощью таблиц Excel.

При подготовке к 9 заданию из ЕГЭ по информатике может быть полезна и прошлогодняя статья.

В 2022 году пошла тенденция давать задачи, в которых применяются знания по математике и геометрии.

Задача (Равнобедренный треугольник)

(№ 4335) (А. Богданов) Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами равнобедренного треугольника. В ответе запишите только число.

Для каждой тройки проверим:

Являются ли числа сторонами треугольника.
Есть ли среди трёх чисел два равных числа.

Чтобы проверить первое условие, нужно вспомнить неравенство треугольника: любая сторона треугольника должна быть меньше суммы двух других сторон.

Поставим «1» в столбце D напротив тех троек, которые подходят под первое условие.

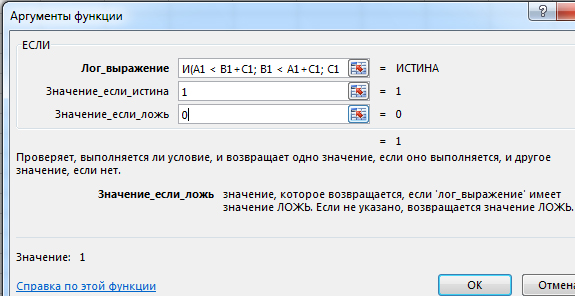
Сначала напишем формулу для первой строчки в ячейке D1.

Кликаем в ячейку D1 и нажимаем кнопку Вставить функцию.

Выбираем функцию ЕСЛИ. Пишем логическое выражение:

Союз И говорит о том, что три условия должны сработать одновременно.

В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

Если одновременно выполняются три условия, то в ячейку идёт 1, иначе 0.

Распространим формулу на весь столбец. Подведём курсор к правому нижнему углу. Как только загорелся чёрный крестик, кликаем два раза, и формула должна распространится на весь столбец.

Возле тех строчек, которые удовлетворяют условию, будут нули, возле тех, которые не удовлетворяют, будут единицы.

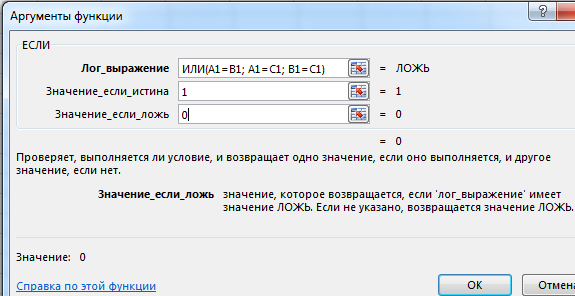
За второе условие будет отвечать столбец E. Напишем условие в ячейку E1.

Союз ИЛИ говорит о том, что если одно условие сработает, значит, выражение будет считаться истинным.

В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

Распространяем всю формулу на весь столбец E. Напротив тех строчек, которые удовлетворяют второму условию, будут стоять «1», в противном случае «0».

В столбце F ставим «1» в тех строчках, где в столбцах D И E одновременно «1», используя функцию ЕСЛИ.

В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.

Выделив столбец F, в правом нижнем углу посмотрим сумму единиц в этом столбце.

Получается ответ 229.

Ещё одна тренировочная задача из ЕГЭ по информатике 2022.

(А. Богданов) Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами тупоугольного треугольника. В ответе запишите только число.

Во-первых проверим: удовлетворяют ли числа условию неравенства треугольника (аналогично прошлой задаче). За это будет отвечать столбец D.

В столбцах E, F, G мы будем вычислять косинусы трёх углов треугольника. Косинусы будем находить по теореме косинусов. Косинусы будем вычислять для всех троек, но учитывать только те, где выполняется неравенство треугольника.

В ячейке E1 напишем формулу:

В ячейке F1 напишем формулу:

В ячейке G1 напишем формулу:

Распространим вышеуказанные формулы на соответствующие столбцы.

Получается примерно такая картина:

Остался последний шаг: проверить, есть ли у какой-нибудь тройки, которая удовлетворяет неравенству треугольника, отрицательный косинус. Тупой угол имеет отрицательный косинус.

Кликаем в ячейку H1, нажимаем кнопку «Вставить функцию» и выбираем ЕСЛИ.

В поле Лог_выражение пишем:

В поле Значение_если_истина ставим «1», в поле Значение_если_ложь ставим «0». Распространяем формулу на весь столбец H, и посчитаем количество единиц в этом столбце.

Количество единиц равно 1720.

Снова нужно знать математические формулы в следующей задаче из примерных вариантов ЕГЭ по информатике 2022.

(А. Комков) Откройте файл электронной таблицы 9-103.xls, содержащей в каждой строке два целых числа – координаты точки на плоскости. Найдите наибольшее расстояние точки от начала координат. В ответе запишите целую часть найденного расстояния.

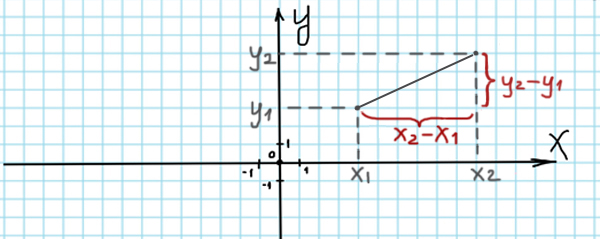
Посмотрим, как найти расстояние от точки с координатами (x1, y1) до точки с координатами (x2, y2).

Здесь работает теорема Пифагора. Здесь s — расстояние между двумя точками.

s 2 = (x2-x1) 2 + (y2-y1) 2

В нашей задаче первая точка — это начало координат, следовательно, x1=0 и y1=0.

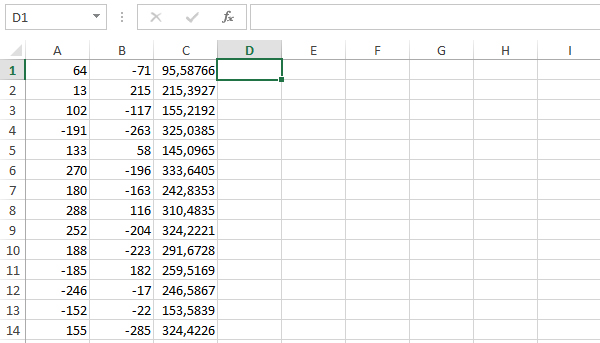
В столбце С получим расстояние от конкретной точки до начала координат.

В ячейке C1 напишем формулу и распространим эту формулу на весь столбец.

Найдём максимальное значение в столбце С. Теперь кликнем в ячейку D1. Нажмём кнопку «Вставить функцию». Выберем функцию МАКС. Укажем мышкой столбец С. Нажмём «ОК».

Целая часть получившегося числа равна 425.

(Е. Джобс) Откройте файл электронной таблицы 9-j1.xls, содержащей показатели высот над уровнем моря географических точек. Найдите среднее значение всех отрицательных показателей и максимальное положительное значение. В качестве ответа укажите целую часть суммы найденных значений.

Эта задача уже не связана c математическими аспектами. Здесь просто достаточно воспользоваться встроенными функциями Excel.

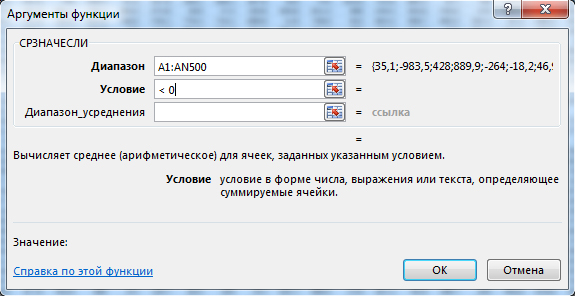
Нужно найти среднее значение только отрицательных значений. Для нахождения среднего значения есть функция СРЗНАЧ. Но нам нужно именно отрицательных значений. Для нахождения среднего значения с условием есть функция СРЗНАЧЕСЛИ. Щёлкним по пустой ячейки и вы

В поле Диапазон мы должны указать все ячейки. Это можно легко сделать с помощью мышки.

В поле Условие укажем »

Среднее значение примерно равно -497,47.

Для определения максимального значения, можно просто воспользоваться просто функцией МАКС, т.к. всё равно максимальное число будет положительным.

Максимальное значение получается 1000.

Сумма равна: 1000 + (-497,47) = 502,53

Целая часть равна 502.

Решим ещё одну old school’ную задачу, которая также полезна при изучении 9 задания из ЕГЭ по информатике 2022.

Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений результат очередного измерения оказывался ниже результата предыдущего на 2 и более градусов.

Внизу под числами представим мысленно область, где будет наше решение.

Таким образом, каждой ячейке соответствует своя ячейка в области решения.

Если выполняется условие задачи (т.е. предыдущее значение больше, чем данное значение на 2 и более градусов), то в соответствующей ячейке из области решения будет стоять «1», в противном случае «0».

Первая ячейка в каждой строчке нуждается в особой формуле, т.к. эта ячейка должна сравниваться с последней ячейкой предыдущей строчки.

Для остальных ячеек формула будет одинаковая, т.к. их значение сравнивается с предыдущем значение, т.е. с левой ячейкой.

Для первой ячейке не будем писать формулу, т.к. ей не с кем сравниваться.

Пишем формулу для строчек в ячейке C94:

Здесь используем функцию ЕСЛИ, как мы делали в предыдущих задачах.

Распространяем эту формулу на всю строчку.

И распространяем на всё пространство (кроме первого столбца)

Важно: Всего должно быть 91 строчка, как и в оригинале.

Теперь составим формулу для первого столбца. Кликаем в ячейку B95. И пропишем формулу:

Распространим данную формулу на весь столбец (на 91 строчку).

Осталось подсчитать количество единиц во всём рабочем пространстве, например, с помощью стандартной функции СУММ.

Количество единиц равно 458.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Как решить задачу с определением трех сторон треугольника?

Задача:
Определите тип треугольника (остроугольный, тупоугольный, прямоугольный) с данными сторонами.
Необходимо вывести одно из слов: «right» для прямоугольного треугольника, «acute» для остроугольного треугольника, «obtuse» для тупоугольного треугольника или «impossible», если входные числа не образуют треугольник.

Чем же плох мой способ?
a = int(input())
b = int(input())
c = int(input())
if pow(c, 2) == pow(a, 2) + pow(b, 2):
print(‘right’)
elif pow(b, 1) + pow(c, 2) — pow(a, 2) > 0:
print(‘acute’)
elif pow(a, 2) + pow(b, 2) Вопрос задан более двух лет назад

4859 просмотров