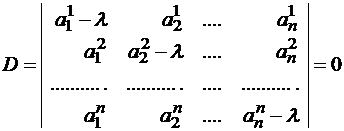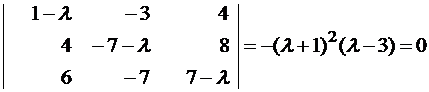Не имеет собственных векторов (3 видео) | Курс школьной геометрии

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 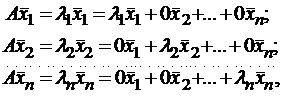тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n — координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)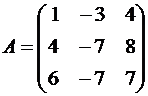
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

Все собственные числа симметрической матрицы вещественны.
Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Видео:Собственные векторы и собственные значения матрицыСкачать

Собственные векторы и собственные значения линейного оператора

Пусть линейный оператор р, действующий в линейном пространстве X над полем Р, имеет в некотором базисе е матрицу А. Ненулевой вектор х G X называют собственным вектором оператора р, если этим оператором он переводится в вектор Хх, т.е. если рх = Л х, где

Л — некоторое число из поля Р, называемое собственным значением оператора р. При этом говорят, что собственный вектор х принадлежит собственному значению А.

Теорема 5.11. Собственными значениями линейного оператора р, действующего в линейном пространстве X над полем Р, являются характеристические корни этого оператора, принадлежащие Р, и только они.

> Пусть линейный оператор р в некотором базисе е имеет матрицу А. Вектор х является собственным вектором линейного оператора р, если выполняется равенство рх = Ах, где А — собственное значение оператора р, отвечающее собственному вектору х. Это равенство можно записать в виде (р — е)х = 0, где ? — тождественный оператор. Переходя к представлению векторов и оператора в заданном базисе, мы приходим к записи этого равенства в матричном виде

где [х] — столбец координат вектора х.

Матричное равенство (5.14) представляет собой однородную систему линейных уравнений относительно элементов столбца [х]. Так как вектор х ненулевой, система (5.14) имеет ненулевые решения, а для этого необходимо и достаточно, чтобы определитель системы был равен нулю, т.е. А — А Е = 0. Это значит, что число А является корнем характеристического многочлена.

Если число А — корень характеристического многочлена, то выполняется равенство А — ХЕ =0. Следовательно, в однородной системе (5.14) определитель равен нулю и эта система имеет ненулевые решения. Каждому такому решению соответствует вектор х, удовлетворяющий условию (р — А е) х = 0, а потому по определению являющийся собственным вектором, которому отвечает собственное значение А. ?

Следствие 5.2. В конечномерном комплексном линейном пространстве собственными значениями линейного оператора являются все его характеристические корни, и только они. В конечномерном действительном линейном пространстве собственными значениями линейного оператора являются все его действительные характеристические корни, и только они.

Из полученного вытекает следующее правило.

Для отыскания всех собственных значений оператора с матрицей А нужно найти все характеристические числа матрицы А и из них выбрать лишь те, которые принадле- жат основному полю, а для отыскания всех собственных векторов оператора с матрицей А нужно для каждого собственного значения А найти все ненулевые решения системы <А —А Е) х = 0.

Алгебраической кратностью собственного значения линейного оператора называют кратность соответствующего корня характеристического многочлена.

Пример 5.8. Для оператора, определенного на действительном линейном пространстве и имеющего в заданном базисе матрицу

найти собственные значения и собственные векторы.

Решение. Характеристический многочлен матрицы А имеет вид:

Его корни Ai = 4 и Л2,з = ±2 г. Так как рассматриваемый оператор действует в действительном линейном пространстве, то его собственным значением будет лишь А = 4. При этом значении А система (А — А Е) X = 0 принимает вид

Ее общее решение можно записать в виде X = (xi,xi,0) T , где х — произвольная постоянная. Если Xi пробегает все действительные значения, то общее решение дает все собственные векторы оператора с матрицей Л, принадлежащие собственному значению А = 4. Других собственных векторов оператор с матрицей А не имеет, так как у него нет других собственных значений.

Теорема 5.12. Множество L собственных векторов линейного оператора р, отвечающих собственному значению А, вместе с нулевым вектором линейного пространства является линейным подпространством.

т.е. вектор х + у является собственным вектором, отвечающим собственному значению Л. Аналогично для любого вектора х € Ь и любого числа а

т.е. вектор ах является собственным вектором, отвечающим собственному значению Л. ?

Следствие 5.3. Любая линейная комбинация собственных векторов линейного оператора р, отвечающих одному и тому же собственному значению Л, является собственным вектором этого оператора, отвечающим тому же собственному значению.

Подпространство Ь, которое образовано собственными векторами, отвечающими собственному значению Л, называют собственным подпространством оператора. Оно представляет собой ядро линейного оператора р — е. Размерность этого подпространства равна п — гд, где п — размерность линейного пространства, в котором действует линейный оператор, а г — ранг линейного оператора р — е.

Подпространство L линейного пространства X называют инвариантным подпространством относительно оператора р, действующего в X, если для каждого вектора х из L его образ рх также принадлежит L. Примерами инвариантных подпространств оператора р являются его собственные подпространства Ь по собственным значениям Л. Так как любой многочлен имеет комплексные или действительные корни, то любой линейный оператор в комплексном линейном пространстве имеет собственные векторы. Значит, у каждого такого оператора есть одномерное инвариантное подпространство. В случае действительного линейного пространства это уже не так: линейный оператор поворота в R.2 на угол д Если действительное линейное пространство X одномерно, то утверждение теоремы тривиально, так как все линейное пространство можно рассматривать как инвариантное подпространство. Поэтому остановимся на случае, когда размерность п линейного пространства не меньше двух.

Если характеристический многочлен линейного оператора 9?, действующего в X, имеет действительные корни, то каждый такой корень является собственным значением. Любой собственный вектор, отвечающий такому собственному значению, порождает одномерное инвариантное подпространство. Таким образом, в этом случае теорема верна.

Пусть характеристический многочлен линейного оператора 9? имеет комплексные (невещественные) корни и = а + г /3 — один из них. Этот корень не является собственным значением оператора 9?, а при таком А система (А — А Е) х = 0, где А — матрица оператора 99 в некотором базисе пространства X, имеет комплексные (невещественные) решения. Представим столбец х в виде х = u + iv, где и и v — столбцы с вещественными компонентами. Подставив х = и+ ivu = a + if3B систему (А — А Е) х = 0, получим

Последнее комплексное равенство распадается на два действительных:

Эти два матричных равенства в совокупности составляют однородную систему действительных линейных уравнений. Поскольку система комплексных уравнений (А — А Е) х = 0 имеет ненулевые решения (определитель этой системы равен нулю), то и система действительных уравнений (5.15) имеет ненулевые решения. Пусть столбцы и и v составляют одно из ненулевых решений. Рассмотрим векторы, координатными столбцами которых являются столбцы и и V. Эти векторы также обозначим через и и v. Покажем, что подпространство L = (и, v) инвариантно относительно оператора 9?.

В силу равенства (5.15) выполняются равенства

Следовательно, образы векторов и п v при действии р принадлежат L. Но тогда и образ любой линейной комбинации векторов и иг принадлежит L. Убедимся в этом непосредственно.

т.е. вектор рх является линейной комбинацией двух векторов ри и pv, принадлежащих подпространству L. Значит рх € L.

В принципе теорема доказана, поскольку подпространство, натянутое на два вектора, имеет размерность не большую двух. Однако отметим, что подпространство L на самом деле двумерное и не может быть одномерным. Последнее возможно лишь в случае, когда векторы и и v линейно зависимы, т.е. когда выполняется равенство и = kv, где к — вещественное число, поскольку векторы и и v с вещественными компонентами. Но тогда это равенство верно и для столбцов координат этих векторов. При этом х = и + iv = (к + i)v, и из равенства (А — Е) х = 0 следует, что столбец v с действительными компонентами является решением системы <А— А Е) v = 0, равносильной системе Av = Л V.

Но система Av = Л г не может иметь действительных решений при комплексном Л, так как для действительного столбца v матричное произведение Av дает столбец с действительными элементами, а произведение Л v имеет комплексные элементы. ?

Заметим, что в силу соотношений (5.15), а также (5.1) и (5.2) матрицей сужения линейного оператора р на подпространство L = = (w, v) в базисе е = (и, v) будет матрица

Теорема 5.14- Пусть линейное пространство X распадается в прямую сумму X = Ь ф Z/2 инвариантных подпространств линейного оператора р, действующего в X. Если е, е%, —

При этом блок А — это матрица сужения оператора р на подпространство Li в базисе е, в2, . а А2 — это матрица сужения оператора р на подпространство L2 в базисе е&+1, щ₊2, . е_п.

> В силу инвариантности подпространства Ь имеем:

Эти разложения означают, что в первых к столбцах матрицы А линейного оператора т , из которого при жз = 1 выделяется частное решение а = (1,2,1) т . Подпространство L = (а) является одномерным инвариантным подпространством оператора (р. При = a + (3i = 2 + i система (А — Ле)ж = 0, т.е. система

имеет общее решение ж = (жь(1 — i) жх, — 2ix) T , из которого при х = 1 выделяется частное решение

где положено и = (1,1,0) г , v = (0, —1, —2) т .

Заметим, что столбцы и = (щ,и2,щ) т и v = <vi,V2,v^) T удобнее находить из однородной системы

с действительными коэффициентами, т.е. из системы

Подпространство L2 = (и, v) является двумерным инвариантным подпространством оператора т к базису е! = (а, и, v) T является матрица

Поэтому в базисе е’ матрицей оператора р будет матрица

Матрицу А’ оператора р в базисе е! можно выписать сразу по следующему правилу:

Геометрической кратностью собственного значения Л линейного оператора р называют размерность собственного подпространства этого оператора, отвечающего собственному значению Л. Можно также сказать, что геометрическая кратность собственного значения — это максимальное число линейно независимых собственных векторов, отвечающих этому собственному значению. Геометрическая кратность 1 собственного значения Л может быть выражена через ранг г линейного оператора р — е: 1 — п — г, где п — размерность линейного пространства.

Теорема 5.15. Геометрическая кратность собственного значения линейного оператора не превышает его алгебраической кратности.

> Пусть в линейном пространстве X действует линейный оператор р, для которого Ао — собственное значение с геометрической кратностью I. В соответствии с определением геометрической кратности существует I линейно независимых собственных векторов ei,

е₂, . ei, отвечающих собственному значению Ао. Систему этих векторов можно дополнить до базиса е, е₂, . е_п в X. В этом базисе матрица линейного оператора имеет вид:

Характеристический многочлен |В — Е по теореме Лапласа можно представить в виде

Отсюда следует, что в характеристическом многочлене |В — А Е корень Ло имеет кратность большую или равную I. Значит, геометрическая кратность I собственного значения Ло не превышает его алгебраической кратности. ?

Если отождествлять оператор с его матрицей, то естественно говорить о собственных значениях и собственных векторах матрицы. На практике так обычно и поступают. Квадратную матрицу называют простой, если для каждого собственного значения матрицы его геометрическая кратность совпадает с алгебраической кратностью. В противном случае матрицу называют дефектной.

Теорема 5.16. Собственные векторы Ь, 62, •••, bk линейного оператора, отвечающие различным собственным значениям Ах, Л2, . А*,, линейно независимы.

О Доказательство проводится методом математической индукции по количеству к собственных векторов. При к = 1 утверждение теоремы очевидно, так как Ъ Ф 0. Допустим, что утверждение верно для систем из к — 1 собственных векторов. Рассмотрим систему 61, 62, . bk и ее линейную комбинацию равную нулю:

Применим к обеим частям этого равенства линейный оператор 1 у = = А у. Если провести еще и комплексное сопряжение, то получим: А*у = А у. Это означает, что левый собственный вектор у матрицы А, принадлежащий собственному значению А, является правым собственным вектором матрицы А* по А, а вектор у — правым собственным вектором матрицы А Т по А. В дальнейшем, говоря о собственных векторах без указаний «правый», «левый», будем понимать, что речь идет о правых собственных векторах.