1) Файловая система Scilab и Текущая папка.
2) Встроенный текстовый Редактор SciNotes.
3) Типы программных файлов.
4) Sce-сценарии.
5) Сохранение, вызов и выполнение сценария, сохраненного в sce-файле.
6) Cохранение и восстановление переменных Рабочей области.
7) Числовые выражения и форматирование их результатов.
8) Логические выражения.
9) Простейшие операторы ввода/вывода данных.
1.2.2. Общее задание
1) Изучить материал учебника [1] (п.п. 1.2, 1.5).
2) Выбрать вариант индивидуального задания из табл. 1.2. 3 -1.
3) Выполнить команды clear и clc для очистки окна Обозревателя переменных и Командного окна.
4) Активизировать Редактор SciNotes.
5) Создать sce —сценарий для выполнения индивидуального задания (вычисление выражений) с использованием встроенных в сценарий функций.
6) Сохранить sce —сценарий в sce-файле со смысловым именем .
7) Провести отладку, исправить ошибки и сохранить сценарий.
8) Загрузить sce —сценарий из sce-файла и выполнить его в Командном окне, предварительно присвоив исходным данным допустимые значения.
9) Модернизировать sce-сценарий, вставив в него операторы ввода исходных данных и вывода результата в форматированном виде.
10) Сохранить sce-сценарий под другим именем, исправить ошибки и выполнить.
11) Создать сценарий для решения поставленной задачи и выполнить его.
12) Сохранить все результаты для отчета.
13) Предоставить результаты работы преподавателю, ответить на поставленные вопросы.
14) Оформить отчет по выполненной работе.
Варианты индивидуальных задани й
| № | Задание |
| 1 | 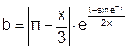 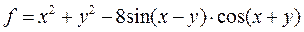 |
| 2 | 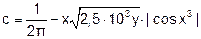 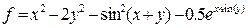 |
| 3 | 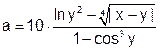 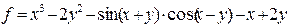 |
| 4 | 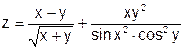 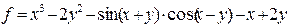 |
| 5 | 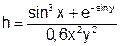 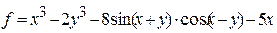 |
| 6 | 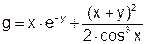 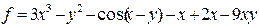 |
| 7 | 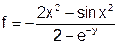 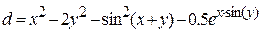 |
| 8 | 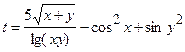 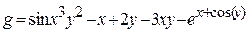 |
| 9 | 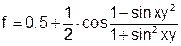 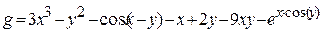 |
| 10 | 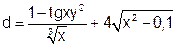 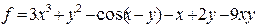 |
| 11 | 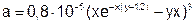 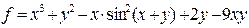 |
| 12 | 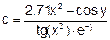 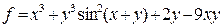 |
| 13 | 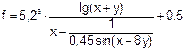 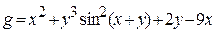 |
| 14 | 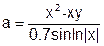 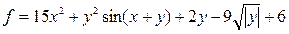 |
| 15 | 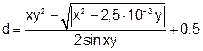 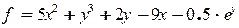 |
| 16 | 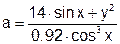 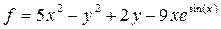 |
| 17 | 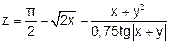 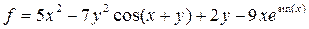 |
| 18 | 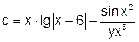 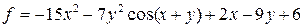 |
| 19 | 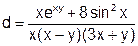 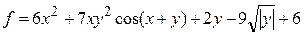 |
| 20 | 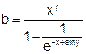 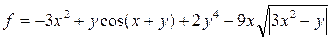 |
| 21 | 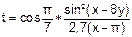 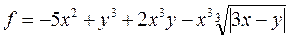 |
| 22 | 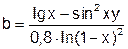 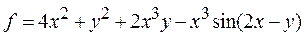 |
| 23 | 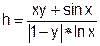 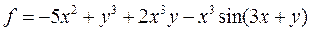 |
| 24 | 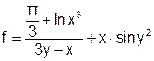 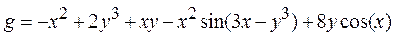 |
| 25 | 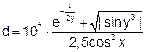 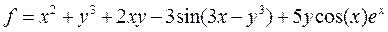 |
| 26 | 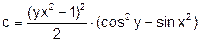 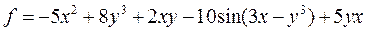 |
| 27 | 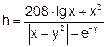 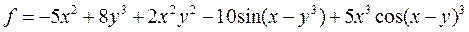 |
| 28 | 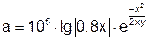 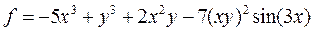 |
| 29 | 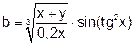 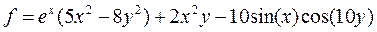 |
| 30 | 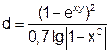 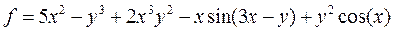 |
Пример выполнения задани я
Пример выполнения задания
1) Решить задачу вычисления арифметических выражений
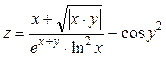
в соответствии с п.п.3-10 общего задания:
2) Результаты выполнения задания (сценарии и протоколы сессии)
//Сценарий Pr 1_2_1. sce вычисления выражений
//Определение функции для вычисления 1-го выражения
//Определение функции для вычисления2-го выражения
function z=f2(x, y)
—>//Протокол сессии Командного окна:
—>// Практическое занятие 1.2 по теме
—>// «Основные объекты системы Scilab»
—>//Присвоение значений,вычисление выражений и вывод результатов
—>// Выполнил:Студент группы БИН1801 Иванов И.И.
—>clear // Очистка окна Обозревателя данных
—>clc // Очистка Командного окна
—>//Загрузка 1-го сценарияPr1_2_1и вызов функций, встроенных в сценарий
—>exec(‘Pr1_2_1.sce’, 0);//Загрузка сценария Pr1_2_1.sceиз текущей папки
—> //Задание начальных значений x и y
—> //Вызов функций f1 и f2, встроенных в сценарий
// Сценарий Pr 1_2_1 mod . sce вычисления выражений
//Определение функции 1-го выражения
//Определение функции 2-го выражения
function z=f2(x, y)
//Ввод исходных данных
//Вычисление значений функций
//Форматирование вывода результата
//Вывод результатов вычисления выражений на экран
—>// Протокол сессии в Командном окне:
—>// Практическое занятие 1.2 по теме
—>// «Основные объекты системы Scilab»
—>// Вариант 0, задание 1 (модифицированное)
—>//Ввод исходных данных, вычисление выражений и вывод результатов
—>// Выполнил: Студент группы БИН1801 Иванов И.И.
—> clear // Очистка окна Обозревателя данных
—> clc // Очистка Командного окна
—>//Загрузка 2-го сценария Pr1_2_1mod
—> exec(‘Pr1_2_1mod.sce’, 0); // Загрузка сценария из текущей папки
Содержание отчета
1) Титульный лист
2) Название и цель практического занятия
3) Общее задание
4) Сценарий, вначале которого должна быть введена информация в виде комментариев:
· имя и назначение сценария;
· вариант индивидуального задания и номер задания.
5) Протокол сессии Командного окна, вначале которого должна быть введена информация в виде комментариев:
· название практического занятия;
· вариант индивидуального задания и номер задания;
· ФИО студента, номер группы;
· краткое перечисление действий, выполняемых во время сессии.
1.2.6. Контрольные вопросы по теме
1) Каким образом открыть новое окно редактора SciNotes?
2) Как в окне Обозреватель файлов сделать нужный каталог текущим?
3) Каким образом открыть в SciNotes ранее созданный файл?
4) Что такое сценарий?
5) Имеет ли сценарий параметры?
6) Допускается ли в SciNotes при вводе текущей строки сценария вернуться к редактированию в предыдущих строках?
7) Какова последовательность действий при сохранении нового сценарий в sce-файле?
8) Каким образом сохранить исправленный текст sce-сценария?
9) Как в редакторе SciNotes осуществляется переход между открытыми окнами, содержащими разные сценарии?
10) Можно ли из одного сценария обращаться к другому?
11) Какой командой, файл, созданный в редакторе SciNotes загрузить в оперативную память?
12) Каким образом в команде exec указывается путь к загружаемому файлу со сценарием?
13) Как и где можно установить текущую папку?
14) Что такое глобальные переменные и когда они используются?
15) Если переменная создана в Командном окне, является ли она видимой для загруженного сценария?
16) Какие переменные являются локальными?
17) Формат оператора ввода данных input?
18) Формат оператора ввода данных x _ dialog?
19) Как с использованием оператора disp осуществить вывод значения переменной или текста можно?
20) Как осуществить вывод результатов вычисления в форматированном виде?
21) Можно ли выполнить сценарий из редактора SciNotes?
1.3 Практическое занятие по теме
« Матри чные операции создания, доступа,
извлечения и модификации »
Цель работы: Изучение способов создания векторов и матриц, операций индексирования, поэлементных выражений с векторами и матрицами.
Вопросы, подлежащие изучению
1) Создание векторов и матриц различного типа.
2) Индексация матриц: векторная, матричная и линейная.
3) Доступ к элементам вектора и матрицы.
4) Матричные операции: арифметических, логических и операций отношения.
5) Функции обработки элементов матриц.
6) Матричная и логическая индексация матриц.
1.3.2 Общее задание
1) Изучить материал учебника [ 1 ] (п.1.3).
2) Выбрать вариант индивидуального задания из табл.1.3-1. Каждое задание содержит две задачи.
3) Выполнить команды clear и clc для очистки окна Обозревателя переменных и Командного окна.
4) Открыть новое окно редактора SciNotes.
5) Создать для выполнения каждой задачи по два сценария. Первый сценарий должен содержать функции, предназначенные для выполнений действий над векторами и матрицами с использованием матричных операций. Второй сценарий предназначен для ввода исходных данных, вызова первого сценария и вывода результатов. Здесь для вывода отдельных значений и пояснений следует использовать функцию mprintf, а для вывода числовых массивов – функции mprintf или disp.
6) Сохранить sce —сценарии в файлах, исправить ошибки.
7) Решить индивидуальные задания, выполнив созданные сценарии.
8) Сохранить все результаты для отчета.
9) Предоставить результаты работы преподавателю, ответить на поставленные вопросы.
10) Оформить отчет по выполненной работе.
Варианты индивидуальных заданий
| № | 1-я задача | 2-я задача |
| 1 | Ввести 3 вектора разной длины и найти сумму отрицательных элементов каждого из них. | В матрице А(3х4)определить произведение элементов, расположенных на нечетных местах в каждой строке. Заменить полученными значениями элементы первого столбца матрицы. |
| 2 | Подсчитать количество «единиц» на четных местах введенного вектора. | В матрице Х(4×5)поменять столбец, в котором находится максимальный элемент, с её первым столбцом. |
| 3 | Найти сумму положительных элементов введенного вектора, стоящих на местах, кратных числу n. | В матрице T(3×5)определить строки, в которых расположено более двух элементов, равных нулю. Заменить все элементы этих строк на 100. |
| 4 | Найти сумму элементов введенного вектора, стоящих на местах кратных трем и больших заданного числа x. | Элементы каждой строки матрицы, значения которых больше среднеарифметического значения данной строки, заменить этим значением. |
| 5 | Найти сумму отрицательных элементов введенного вектора, расположенных на нечетных местах. | Все отрицательные элементы матрицыС(3х4) умножить на х1, а положительные – разделить на х2. Подсчитать количество нулевых элементов. |
| 6 | Найти произведение элементов введенного вектора, больших или равных, введенному значению х. | В введенной матрице Ввсе элементы, модули которых равны модулям максимального или минимального элемента, заменить значением y. |
| 7 | Найти сумму последних n элементов введенного вектора, меньших числа х. | Найти сумму элементов прямоугольной матрицы D, не лежащих в интервале [a,b]. Заменить этим значением все элементы, попавшие в этот интервал. |
| 8 | Среди n первых элементов введенного вектора найти сумму отрицательных элементов. | Элементы квадратной матрицы ниже главной диагонали уменьшить на х1 , а элементы выше главной диагонали увеличить на х2. |
| 9 | Найти сумму и количество элементов введенного вектора, больших числа х. | Найти количество отрицательных элементов в каждой строке квадратной матрицы F(nxn)и заменить полученными значениями элементы главной ее диагонали. |
| 10 | Подсчитать количество элементов введенного вектора, принадлежащих интервалу [a,b]. | В матрице А(4×5)определить столбцы, в которых все одинаковые элементы. Заменить элементы этих столбцов случайными целыми числами от 0 до 100. |
| 11 | Найти первый отрицательный элемент введенного вектора и вывести его номер и значение. | Максимальный элемент каждой строки матрицы D(4,4)заменить числом х. |
| 12 | Найти количество элементов введенного вектора, меньших единицы. | Найти среднегеометрическое значение элементов каждого столбца квадратной матрицы и заменить им элементы главной диагонали матрицы Y. |
| 13 | Найти количество нулевых элементов введенного вектора среди его последних n элементов. | В каждой строке матрицы К(m×n) найти количество элементов больше х1и заменить их на значение последнего элемента строки. Вывести полученную матрицу по столбцам. |
| 14 | Найти произведение ненулевых элементов вектора. | Минимальный элемент в каждом из столбцов матрицы заменить нулевым значением. |
| 15 | Найти произведение положительных элементов вектора, расположенных на нечетных местах. | В матрице поменять строку, в которой находится минимальный элемент, с последней строкой. |
| 16 | Определить среднее значение всех отрицательных элементов вектора Р. | В матрице определить строки, в которых не все элементы одинаковы. Увеличить элементы этих строк на значение х. |
| 17 | Найти сумму элементов вектора, не попавших в интервал [a,b]. | В матрице определить сумму отрицательных элементов каждого столбца. Заменить полученными значениями элементы второй строки. |
| 18 | Найти сумму отрицательных элементов вектора на четных местах. | Найти среднее арифметическое значений элементов матрицы A(nxn)и заменить этим значением элементы последней строки и последнего столбца. |
| 19 | Определить сумму положительных и произведение отрицательных элементов вектора. | В матрице определить столбцы, в которых расположено более двух нулевых элементов. Заменить элементы в этих столбцах назначение х. |
| 20 | Определить количество элементов вектора, кратных x. | Элементы каждого столбца матрицы, которые меньше среднеарифметического значения данного столбца, заменить этим значением. |
| 21 | Найти максимальное значение среди элементов вектора между номерами n1 и n2. | В вещественной матрице определить суммы элементов, расположенных на нечетных местах в каждой строке. Заменить полученными значениями элементы последнего столбца матрицы. |
| 21 | Найти общее количество элементов вектора, равных х1и х2. | Максимальные элементы матрицы (их может быть несколько) увеличить на среднее значение всех элементов, расположенных выше главной диагонали. |
| 22 | Найти предпоследний отрицательный элемент введенного вектора Х. | Все элементы матрицы, кратные х, заменить минимальным значением элемента матрицы. |
| 23 | Подсчитать сумму и произведение первых n положительных элементов введенного вектора. | Во введенной матрице заменить все элементы, равные числу х, на среднее значение элементов матрицы. |
| 24 | Определить номер минимального по модулю элемента вектора-столбца. | Найти количество элементов матрицыС(5х5), лежащих в интервале [a,b], и заменить этим значением элементы, лежащие на главной диагонали. |
| 25 | Найти наибольший отрицательный элемент вектора. | Найти произведение положительных элементов главной диагонали квадратной матрицы А. Заменить полученным значением все отрицательные элементы матрицы. |
| 26 | Подсчитать сумму квадратов четных и сумму квадратов нечетных элементов вектора. | В матрице определить произведения элементов, расположенных на четных местах в каждом столбце. Заменить полученными значениями элементы первой строки матрицы. |
| 27 | Вывести значение и номер последнего нечетного отрицательного элемента вектора. | Элементы матрицы уменьшить на минимальное значение её элементов, кратных х. |
| 28 | Определить элемент вектора, наиболее близкий по своему значению к заданному x. | В матрице симметрично поменять между собой элементы выше главной диагонали с элементами ниже главной диагонали, а элементы главной диагонали расположить в обратном порядке. |
| 29 | Определить первый максимальный элемент вектора и заменить его нулем. | Для матрицы А найти среднее арифметическое сумм элементов, расположенных над и под главной диагональю. |
| 30 | В векторе Х поменять местами минимальное и максимальное значения элементов. | Ввести квадратную матрицу и получить из ее элементов другую, каждый элемент которой умножен на значение ее определителя. |
Примеры выполнения задани й
Пример выполнения задания 1
1) В соответствии с п.п.5-7 общего задания решить задачу 1: Среди n последних элементов вектора найти количество элементов, равных вводимому
Видео:Пример программы для нахождения суммы отрицательных элементов массива. Программирование на С++Скачать

Векторы на ЕГЭ по математике. Действия над векторами
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения 
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Вот другой пример.
Автомобиль движется из A в B . Конечный результат — его перемещение из точки A в точку B , то есть перемещение на вектор 
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1 . Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y , абсцисса и ордината.
Вектор также задается двумя координатами:
Здесь в скобках записаны координаты вектора 
Находятся они просто: координата конца вектора минус координата его начала.
Если координаты вектора заданы, его длина находится по формуле
Видео:Задачи с массивами | Pascal | Сумма и поиск элементовСкачать

Сложение векторов
Для сложения векторов есть два способа.
1 . Правило параллелограмма. Чтобы сложить векторы 



Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
2 . Второй способ сложения векторов — правило треугольника. Возьмем те же векторы 



По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
Представьте, что вы идете из пункта А в пункт В , из В в С , из С в D , затем в Е и в F . Конечный результат этих действий — перемещение из А в F .
При сложении векторов 

Видео:C++ | Сложение элементов массиваСкачать

Вычитание векторов
Вектор 



Теперь понятно, что такое вычитание векторов. Разность векторов 



Видео:accumulate c++ | сумма и произведение элементов массива | Библиотека (stl) C++ #19Скачать

Умножение вектора на число
При умножении вектора 



Видео:Язык C++ с нуля | #31 Поиск элементов массива в c++Скачать

Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 

Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
Видео:Язык C++ с нуля | #33 Найти максимальный и минимальный элемент массива в c++Скачать

Программирование в среде MATLAB
1. Программирование в среде MATLAB
Написать файл-функцию с использованием операторов ветвления и циклов, на основании вариантов задания. Вывести в командное окно исходные и расчётные данные, используя команды форматного вывода.
1. Найти произведение отрицательных элементов массива.
2. Подсчитать количество «единиц», стоящих на чётных местах массива.
3. Найти сумму положительных элементов массива, стоящих на местах, кратных 5.
4. Найти сумму элементов массива, больших 5, стоящих на местах кратных трём.
5. Найти сумму отрицательных элементов массива, расположенных на нечётных местах.
6. Найти произведение элементов массива, больших или равных 2.
7. Найти сумму последних пяти элементов массива, меньших 5.
8. Среди n первых элементов массива найти сумму отрицательных элементов.
9. Найти сумму и количество элементов массива, больших единицы.
10. Подсчитать количество элементов массива, попавших в интервал [a, b].
11. Найти первый отрицательный элемент массива, вывести его номер и значение.
12. Найти количество элементов массива, меньших единицы.
13. Найти количество нулевых элементов массива среди последних 5-и его элементов.
14. Найти произведение ненулевых элементов массива.
15. Найти произведение положительных элементов массива, расположенных на нечётных местах.
16. Заменить отрицательные элементы вектора суммой модулей всех его отрицательных элементов.
17.Заменить положительные элементы вектора суммой вех его отрицательных элементов.
18. Заменить максимальный элемент вектора средним значением всех его элементов.
19. Вычислить произведение элементов вектора, не превосходящих среднее арифметическое значение модулей его элементов.
20. Для заданного вектора найти наибольшее значение и вычесть его из всех элементов вектора. Вывести исходный и преобразованный вектора.
21. Для заданного вектора найти наименьшее значение и прибавить его ко всем элементам вектора. Вывести исходный и преобразованный вектора.
22. Для заданного вектора найти наибольшее значение и умножить на него все элементы вектора. Вывести исходный и преобразованный вектора.
23. . Для заданного вектора найти наименьшее значение и умножить на него все элементы вектора. Вывести исходный и преобразованный вектора.
24. Для заданного вектора найти наибольшее значение и разделить на него все элементы вектора. Вывести исходный и преобразованный вектора.
25. . Для заданного вектора найти наименьшее значение и разделить на него все элементы вектора. Вывести исходный и преобразованный вектора.
26. Найти сумму элементов массива, больших 5, стоящих на местах кратных трём.
27. Среди n первых элементов массива найти сумму отрицательных элементов.
28. Найти первый отрицательный элемент массива, вывести его номер и значение.
2. Простые вычисления.
Вывести графики заданных функций одновременно на одном графике в декартовых координатах (plotyy). Для разных графиков использовать разный тип и цвет линий. Графики необходимо подписать.
📹 Видео
Решение задач на массивы в языке c++ | Практика на c++ урок 1.Скачать

КАК РАБОТАЮТ ЧИСЛА С ПЛАВАЮЩЕЙ ТОЧКОЙ | ОСНОВЫ ПРОГРАММИРОВАНИЯСкачать

Скалярное произведение векторов. 9 класс.Скачать

#635 НАУКА Структура вакуума. Устройство Мироздания: версия Межзвездного Союза. Юмор в разных мирах.Скачать

Найти минимальный элемент массива. Поиск минимального элемента в массиве. C++ для начинающих. ДЗ#8.Скачать

Обработка матриц - расчет количества отрицательных элементов столбцаСкачать

НАЙТИ СУММУ ЧЕТНЫХ ЧИСЕЛ В МАССИВЕ C# | РАБОТА С МАССИВАМИ | СИ ШАРП УРОКИ | ДОМАШНИЕ ЗАДАНИЯ # 8Скачать

Работа с массивом в 1С: считаем сумму элементов массиваСкачать

7 10 Найти количество отрицательных элементов массиваСкачать

Как найти сумму n чисел PythonСкачать

сортировка отрицательных элементов массиваСкачать

Вычитание векторов. 9 класс.Скачать

Информатика 9 класс. ВЫЧИСЛЕНИЕ СУММЫ ЭЛЕМЕНТОВ МАССИВА (УМК БОСОВА Л.Л., БОСОВА А.Ю.)Скачать

Задача2 Бл-сх С++ Mathcad Двумерный массив задан из файла, найти S сумму отрицательных элементовСкачать

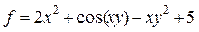



















 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»