Рассмотрим два важных способа описания линейных подпространств, которые условно будем называть внутренним и внешним. В первом (внутреннем) способе используется понятие линейной оболочки векторов, когда все элементы подпространства выражаются через некоторые его элементы (образующие). При втором (внешнем) способе применяются однородные системы уравнений. В этом случае подпространство описывается как пересечение некоторых содержащих его множеств. Для каждого способа описания подпространств укажем методики на хождения размерностей, базисов, алгебраических дополнений, пересечений и сумм подпространств.
Любое n-мерное вещественное линейное пространство изоморфно n-мерному арифметическому пространству . Чтобы установить изоморфизм , достаточно выбрать в пространстве базис и каждому вектору поставить в соответствие его координатный столбец. Поэтому в данном разделе будем рассматривать описание подпространств n-мерного арифметического пространства .
Первый (внутренний) способ. Пусть в пространстве заданы столбцы . Напомним, что для систем столбцов были определены понятия базы (максимальной линейно независимой подсистемы столбцов) и ранга (максимального числа линейно не зависимых столбцов системы), а также методы их нахождения.
Рассматривая линейную оболочку столбцов как линейное подпространство , заключаем, что база системы столбцов является базисом этого подпространства, а ранг системы столбцов равен размерности подпространства .
Поэтому для нахождения размерности и базиса подпространства нужно выполнить следующие действия:
1) составить из данных столбцов матрицу размеров ;
2) привести ее к ступенчатому виду (1.4), используя элементарные преобразования строк;
3) определить размерность и базис подпространства
– количество ненулевых строк в матрице равняется размерности подпространства, т.е. ,
– столбцы матрицы , содержащие единичные элементы (в начале каждой «ступеньки»), определяют номера линейно независимых столбцов матрицы , т.е. искомый базис.
Таким образом, если подпространство задано своими образующими , то его размерность равна рангу системы столбцов , т.е. , а базисом служит максимальная линейно независимая подсистема образующих.
Второй (внешний) способ. Пусть подпространство задано как множество решений однородной системы уравнений с неизвестными. Множество решений системы уравнений можно рассматривать как пересечение подпространств , где — множество решений i-го уравнения системы . Напомним, что любое решение однородной системы представляется в виде линейной комбинации элементов фундаментальной системы решений. Поэтому раз мерность пространства , а базисом служит фундаментальная система решений однородной системы . Способы нахождения фундаментальной системы решений рассмотрены ранее.
Видео:Линал 2.2. Линейная оболочкаСкачать

Переход от одного способа описания подпространств к другому
Переход от внутреннего описания к внешнему. Пусть подпространство задано линейной оболочкой столбцов . Требуется составить такую однородную систему уравнений, множество решений которой совпадает с , т.е. . Для этого нужно выполнить следующие действия.
1. Из данных столбцов составить матрицу размеров , а затем блочную матрицу , приписав к матрице единичную матрицу n-го порядка.
2. Элементарными преобразованиями над строками блочной матрицы и первыми ее столбцами привести матрицу к виду , где — простейший вид матрицы .
3. Из последних строк матрицы составить матрицу .
4. Записать искомую систему уравнений .
Поясним содержание алгоритма. Заданное подпространство состоит из линейных комбинаций данных векторов, т.е. все его элементы имеют вид . Решаемую задачу можно сформулировать так: для каких векторов найдутся такие числа , чтобы выполнялось равенство . Другими словами, при каких неоднородная система ( уравнений с неизвестными ) имеет решения? Используя необходимое и достаточное условие (5.24) совместности системы, получаем равенство . Заметим, что решение поставленной задачи неоднозначно, так как существует много однородных систем, имеющих од но и то же множество решений.
Пример 8.8. Подпространство задано линейной оболочкой столбцов . Составить систему уравнений, определяющую подпространство .
Решение. 1. Составляем матрицу и блочную матрицу:
2. Приводим левый блок к простейшему виду. Вычитаем первую строку из остальных, а затем к четвертой строке прибавляем вторую, умноженную на (-2):
Преобразовываем столбцы левого блока: ко второму столбцу прибавим пер вый, умноженный на (-1), к третьему столбцу прибавим первый, умноженный на (-3), а затем второй, умноженный на (-1). Эти преобразования не изменяют правый блок полученной матрицы. Находим простейший вид Л матрицы и матрицу
3. Из последних строк матрицы составляем матрицу искомой системы.
4. Записываем систему уравнений Заданные в условии примера столбцы являются решениями полученной системы, в чем можно убедиться при их подстановке в систему уравнений вместо .
Переход от внешнего описания к внутреннему. Пусть подпространство задано как множество решений однородной системы т уравнений с л неизвестными: . Требуется найти размерность и базис этого подпространства, т.е. представить его в виде линейной оболочки . Для этого нужно выполнить следующие действия.
1. Найти фундаментальную систему решений однородной системы . Искомая размерность .
2. Представить заданное пространство как линейную оболочку .
Первый пункт алгоритма удобно выполнять следующим образом:
– составить блочную матрицу , приписав к матрице единичную матрицу n-го порядка;
– элементарными преобразованиями над столбцами блочной матрицы и строками верхнего блока привести матрицу к виду , где — простейший вид матрицы ;
– из последних столбцов матрицы составить фундаментальную матрицу .
Столбцы фундаментальной матрицы составляют искомую фундаментальную систему решений.
Заметим, что решение поставленной задачи неоднозначно, так как существует много базисов одного и того же линейного подпространства.
Пример 8.9. Найти размерность и базис подпространства , заданного системой уравнений
Решение. 1. Фундаментальная матрица для этой системы была найдена в примере 5.6
Ее столбцы образуют фундаментальную систему решений. Размерность подпространства равна , .
2. Столбцы являются искомым базисом, так как они линейно независимы и .
Видео:Линейная оболочка. Базис и размерностьСкачать

Линейные подпространства
Подмножество L линейного пространства X над полем Р называют линейным подпространством этого пространства, если оно само является линейным пространством относительно введенных в X операций сложения векторов и умножения векторов на числа из поля Р.
Для того чтобы подмножество L линейного пространства X было его линейным подпространством, необходимо и достаточно, чтобы оно было замкнуто относительно операций сложения векторов и умножения векторов на числа из поля Р, т.е. чтобы выполнялись следующие условия:
- 1) для любых векторов а и Ъ из L их сумма а + b также принадлежит L;
- 2) для любого вектора а из L и любого числа а 6 Р вектор а а принадлежит L.
Действительно, эти условия означают, что операции в линейном пространстве X можно рассматривать и как операции на множестве L. При этом будут верны все аксиомы, кроме третьей и четвертой. Выполнение третьей аксиомы равносильно утверждению, что при выполнении условий 1 и 2 нулевой вектор принадлежит L, а выполнение четвертой означает, что для любого вектора ж € L противоположный вектор —х принадлежит L. Первое из этих утверждений следует из равенства 0 = 0 • ж, где в качестве х можно взять любой вектор в множестве L. Второе утверждение — следствие равенства — х = ( — 1) • х.
Условия 1 и 2 можно объединить в одно условие: для любых векторов множества L их линейная комбинация с произвольными коэффициентами принадлежит L.
Приведем примеры линейных подпространств.
- 1. Множество векторов на прямой или на плоскости является подпространством в обычном трехмерном пространстве.
- 2. Множество многочленов степени нс выше второй является подпространством в линейном пространстве многочленов степени не выше третьей.
- 3. Множество решений однородной системы линейных уравнений с п неизвестными является подпространством в линейном п-мерном арифметическом пространстве Кп.
Пусть в линейном пространстве X над полем Р дана система векторов di, о,2, . ak. Множество всевозможных линейных комбинаций ац ai+a2 a2 + . +ak dk этой системы называют линейной оболочкой системы векторов а, а2, . а*,.
Линейная оболочка L системы векторов а, а2, . ак является подпространством в X. Действительно, если векторы а и b принадлежат L. т.е. имеют представления
то и векторы a + b и Л а имеют вид
Следовательно, они принадлежат L.
Линейную оболочку L системы векторов а, Действительно, размерность конечномерного линейного пространства L может быть определена как максимальное количество линейно независимых векторов в этом пространстве. Очевидно, что максимальное количество линейно независимых векторов в любом подмножестве L в X не превышает максимального количества линейно независимых векторов в X. Отсюда и следует утверждение теоремы. ?
Любое конечномерное линейное пространство порождается конечной системой векторов, например любым своим базисом. Согласно доказанной теореме это верно и для всякого линейного подпространства линейного пространства.
Теорема 4-^1. Пусть L — подпространство п-мерного линейного пространства X. Любой базис а, 0,2, . а/с в L можно дополнить до базиса а, 02, «ь а к+ъ •••> а п всего линейного пространства X, причем линейному подпространству L принадлежат те и только те векторы, которые в указанном базисе имеют столбцы координат вида
> Действительно, любой базис в L, как и вообще любую линейно независимую систему векторов в X, можно дополнить до базиса линейного пространства X. Если вектор х имеет столбец координат (4.3С), то он имеет представление
и, следовательно, принадлежит L как линейная комбинация векторов из L. Если вектор х принадлежит L, то он может быть разложен по базису 0,1, о2, . ак:
Это разложение в то же время является разложением вектора х в базисе oi, 02, . ап линейного пространства X, дающим столбец координат вида (4.3С). ?
Теорема 4-22. Пусть X — конечномерное линейное пространство и в нем задан базис е. Тогда для любого линейного подпространства L в X можно указать такую однородную систему линейных уравнений Ах = 0, что множество координатных столбцов всех векторов из L в базисе е будет совпадать с множеством всех решений системы Ах = 0.
О Пусть е = (ei, ег. еп) — заданный базис в X. Выберем в L некоторый базис а, 02, . ак и дополним его векторами ак+1, ак—2,
. ап до базиса в X. Пусть в этом базисе произвольный вектор х из L имеет координаты х, х’2, . х’к, х’к+1, . х’п. Из теоремы 4.21 вытекает, что подпространство L в базисе а = (ai,a2. ап) описывается однородной системой уравнений х‘к+1 = 0, х‘к+2 = 0, . х’п = 0.
Применяя формулу х’а = Т
1 хе преобразования координат (см. формулу (4.24) в п. 4.6), которая в подробной записи имеет вид
описывающую линейное подпространство L в базисе е. ?
Заметим, что если подпространство L имеет размерность к, то ранг полученной системы равен п—к, поскольку строками ее матрицы служат п — к строк матрицы Т -1 , в которой любая подсистема строк линейно независима.
Однородную систему линейных уравнений, описывающую данное линейное подпространство L, называют общими уравнениями этого подпространства. Общие уравнения подпространства определяются неоднозначно: достаточно систему линейных уравнений, описывающую подпространство, заменить любой эквивалентной системой, чтобы получить другие общие уравнения того же подпространства. Вид общих уравнений подпространства, получаемых с помощью процедуры, указанной в доказательстве теоремы 4.22, зависит от выбора базиса в L и выбора векторов, дополняющих этот базис до базиса в пространстве X.
При мер 4.18. Составить общие уравнения линейного подпространства L = (ai,a2) в четырехмерном линейном пространстве X, если векторы а и а2 заданы своими координатами в некотором базисе е: [а]е = (1,1,2,0) т , [а2е = (1,-1,0,2) т .
Решение. Нетрудно убедиться в том, что система векторов а и а2 линейно независима, и потому составляет базис в линейном подпространстве L. Дополним эту систему векторов до базиса в линейном пространстве X векторами [аз]е = (0, 0,1,0) т и [ац]е = (0,0,0,1) т . Пусть в этом базисе произвольный вектор ж из L имеет координаты х‘2, Ж3, х4. В базисе а, а2, cl-j, 0,4 линейное пространство L описывается системой уравнений х‘3 = 0, х4 = 0. Матрицей перехода от базиса е к новому базису а = (сч,а2 ,аз,а4) является матрица
обратной к которой является матрица
В силу теоремы 4.21, линейное подпространство в базисе а описывается однородной системой уравнений
Применив формулу преобразования координат х’а = Т 1 хе, которая в данном случае в подробной записи имеет вид
систему х‘3 = 0, х‘4 = 0 преобразуем в систему 
Если бы в качестве векторов аз и бц взяли векторы [аз]е = (0,0, — 1, —1) т , [ai]e = (0,0, —1,1) т , то повторив все вычисления, получили бы систему линейных уравнений
определяющую линейное подпространство L в базисе е. ?
Если подпространство задано общими уравнениями, то для построения базиса этого подпространства следует построить фундаментальную систему решений для общих уравнений подпространства.
При мер 4.19. Найти какой-либо базис подпространства L, заданного системой уравнений
Решение. Выбрав в качестве главных неизвестные х, Х2, а свободных — хз, Х4, решим систему. В результате получим общее решение
Фундаментальную систему решений рассматриваемой однородной системы линейных уравнений составляют столбцы (—1,0,1,0) т , (0,-1, 0,1) т , а базис линейного пространства решений — векторы, которые в заданном базисе имеют указанные столбцы координат. ?
Если ai, с*2, . dfc — базис линейного подпространства L в линейном пространстве X, то L можно задать уравнением
которое называют параметрическим уравнением подпространства L в векторной форме.
Пусть векторы oi, При мер 4.20. Подпространство L = (ai, т , т , задать параметрическими уравнениями (4.37) и (4.38) и общими уравнениями.
Решение. Векторное уравнение (4.37) в данном случае имеет
Переходя к координатам, получаем координатную форму параметрических уравнений
Исключив параметры ?1 и ?2, получим общие уравнения подпространства L:
Пусть в линейном пространстве X даны подпространства L и L2. Множество Ь П L2 векторов, принадлежащих как Ь, так и L2, является подпространством в X. Его называют пересечением подпространств Li И 1/2-
Множество всех векторов х вида х = а + 6, где а € L, Ъ ? 1>2 называют суммой подпространств Ь и L2 и обозначают через
L1+L2. Если при этом пересечение ЬГЬ2 — нулевое подпространство, то сумму L + L2 называют прямой суммой и обозначают через L ® Z/2-
Сумма подпространств является подпространством. Действительно, пусть х = а + 6, у = с + d, где а, с € Li, b,d е L2. Тогда х + у = — (а -|- с) -Ь (6 с?) ? L -Н J
Аналогично для любого числа а имеем: ах = аа + ab € L + L2, так как аа € Li и аб € L2.
Понятия пересечения и суммы подпространств распространяются на любое число подпространств.
Если сумма L +L2 подпространств L и L2 в X является прямой, то представление любого вектора х в виде х = а+Ь, где a ? L, 6 € L2, единственно. В частном случае, когда X = Ь ф L2, также каждый вектор х ? X имеет единственное представление х = а + Ь, где а ? Li, 6 ? Дг. В этом случае подпространства Ь и L2 называют прямыми дополнениями друг друга, а слагаемое а ? Ь — проекцией вектора х на подпространство Ь параллельно подпространству
Пример 4.21. В пространстве X = К4 построить какое-либо прямое дополнение Дг к подпространству L = (ai,a2), где а = (1, 1,1,0) т , аг = (1,0,1,0) т и найти проекцию вектора х = (2,1,5,5) т на Li параллельно L2.
Решение. Векторы ai и аг линейно независимы и поэтому составляют базис в подпространстве Ь. Дополним систему векторов а, т и 62 = (0,0,0,1) т и положим L2 = (61,62)- Очевидно, что L/2 является искомым подпространством. Далее запишем векторное равенство
перейдем от него к покоординатным уравнениям (см. разд. 4.2) и, решив систему этих уравнений, найдем: оц = «2 = 1, fi = 3, Р2 = 5. Поэтому
где (2,1,2,0) т € Ь, (0,0,3,5) т € L2. Следовательно, проекцией вектора х = (2,1,5,5) т на подпространство L параллельно подпространству L/2 является вектор х = (2,1,2,0) т . ?
Пусть Ь = («1, а2, •••, о-к), 1^2 = (bi, 62,6*) — подпространства в линейном пространстве X. Чтобы найти какой-либо базис в подпространстве L + L2, следует выделить какую-либо максимальную линейно независимую подсистему системы векторов а, а2, . a*,, 6i, 62, 6^. Для этого достаточно составить матрицу из координатных
столбцов этих векторов и в этой матрице выделить какой-либо базисный минор. Векторы, на координатных столбцах которых находится базисный минор, образуют базис в подпространстве L1+L2. Отметим, что базисный минор можно выбирать не в исходной, а в преобразованной матрице (после выполнения последовательности элементарных преобразований строк).
При мер 4.22. Найти базис суммы L + L2 подпространств Li = (01,02,03) и ?2 = <bi,h,h),если т , и2 = (1,1, -1,
Решение. Составим матрицу
Проводя элементарные преобразования строк матрицы, приведем ее к ступенчатому виду:
Видим, что ранг матрицы равен четырем, а один из ее базисных миноров располагается на векторах ai, a2, аз, 6i. Следовательно, эти векторы составляют базис суммы L + L2. ?
Если пространства L и L2 заданы однородными системами уравнений, то пересечение Ь П L2 будет определяться системой, получаемой объединением всех уравнений двух систем. Любая фундаментальная система решений такой системы уравнений дает базис пересечения L Г)Ь2.
Пример 4.23. Найти базис пересечения подпространства Ь, заданного системой уравнений
и подпространства L2, заданного системой уравнений
Решение. Составим объединенную систему уравнений
и найдем ее общее решение
Здесь три свободных неизвестных: Х4 , Xq, Xq. Поэтому каждая фундаментальная система решений этой системы состоит из трех решений. Одну из фундаментальных систем решений составляют столбцы
Они и представляют собой один из базисов подпространства Ь П L2.
Если подпространства L и L2 заданы как линейные оболочки систем векторов
то при построении базиса пересечения L П L2 этих подпространств достаточно перейти к описанию этих подпространств общими уравнениями, а затем действовать, как в последнем примере: объединяя две однородные системы в одну, искать фундаментальную систему решений объединенной системы.
Существуют и другие способы построения базиса пересечения. Например (см. [21], решение задачи 1319), можно составить векторное уравнение
с неизвестными ai, од, . од, Pi, P2, • ••, Pi и от него перейти к системе покоординатных уравнений. Это линейная однородная система. Построив фундаментальную систему решений этой системы, для каждого решения из ФСР вычислим, например, левую часть векторного уравнения (4.39). Получим систему векторов, порождающую линейное пространство L П L2. Теперь базис в L П L2 можно построить, выделив в этой системе векторов максимальную линейно независимую подсистему. Отметим, что если система векторов 01, Пример 4.24. Найти базис пересечения подпространств Ь =
Решение. Сначала используем первый способ, переходя к общим уравнениям подпространств. Подпространство L описывается параметрическим уравнением х = t а + t2 0,2 + Сз «з, которое в координатной форме имеет вид:
Исключив параметры t, 12, ?3, придем к общему уравнению х — —Х2 — х3 + х4 = 0 подпространства L. Аналогично получаем общее уравнение Х — Х2 — х3 — х4 = 0 подпространства />2- Общие уравнения подпространства L П L2 имеют вид:
Фундаментальную систему решений этой системы составляют, например, векторы Х = (1,0,1, 0) т , Х2 = (0,1, 0,1) т . Эти векторы образуют базис в подпространстве Ь П L2.
Теперь применим второй способ решения примера. Составим векторное уравнение
в подробной записи имеющее вид:
Переходя к покоординатным уравнениям, получим однородную систему
с шестью неизвестными. Ее общее решение таково:
Свободных неизвестных два, и фундаментальная система решений состоит из двух столбцов
В этих двух столбцах выбираем первые три компоненты и принимаем их в качестве значений 04, o2, ад в выражении ац а + а2 + од «3. Получаем два вектора
составляющих базис подпространства L П L2. ?
Теорема 4-23. В конечномерном линейном пространстве X размерность суммы L + L2 подпространств Li w L2 равна сумме размерностей этих подпространств минус размерность их пересечения, т.е.
> В подпространстве LCL,2 выберем какой-либо базис е = (ei, 62, . еД. Эта система векторов линейно независима и одновременно принадлежит и L1, и L2. Дополним ее до базиса в Ь системой векторов / = (Л, /2, •••,//) и до базиса в L2 системой векторов д = (дг, д2 ,дт)- Из трех систем векторов составим объединенную систему
и докажем, что она является базисом в L + L2.
Через систему векторов (е,/, д) линейно выражается любой вектор 2 ? L +1/2- Действительно, для вектора 2 имеет место представление z = х + у, где х Е Z/i, у ? Ь2. Вектор х линейно выражается через систему (е,/), а вектор у — через систему (е,д). Поэтому их сумма z линейно выражается через объединенную систему (e,f,g).
Система векторов (е, f,g) линейно независима. Чтобы доказать это, запишем равенство
и покажем, что оно возможно только при нулевых значениях всех коэффициентов. В равенстве (4.41) объединим слагаемые, относящиеся к векторам систем ей/:
Вектор а принадлежит подпространству L. Но из равенства (4.41) следует, что
и вектор а принадлежит подпространству L2. Значит, а 6 L (IL2. Но из этого условия вытекает, что вектор а линейно выражается через систему векторов е, т.е. имеет место представление а = ц е +. + ць е*,. Это представление можно рассматривать как разложение вектора a Е Е L по базису (е, /). В силу единственности разложения по базису заключаем, что оба разложения совпадают, т.е. = оц, . /2/с = аь, /?1 = . = Pi = 0. С учетом полученных соотношений равенство (4.41) принимает вид
Поскольку система векторов (е,д) линейно независима (как базис в Z/2), это равенство возможно лишь при нулевых значениях всех коэффициентов:
Таким образом, доказано, что равенство (4.41) выполняется лишь при нулевых значениях всех коэффициентов, а система (е, /, д) линейно независима и является базисом в подпространстве Ь + L2. Число векторов в этом базисе, а потому и размерность пространства L + L2, равна к + I + т. Поскольку cliniLi — к + I, dim L2 = к + т, dim(Li П L2) = к, то
Видео:Линейная зависимость векторовСкачать

Учебное пособие: Методические указания для студентов 1 курса Одесса 2008
| Название: Методические указания для студентов 1 курса Одесса 2008 Раздел: Остальные рефераты Тип: учебное пособие Добавлен 17:40:19 17 сентября 2011 Похожие работы Просмотров: 2273 Комментариев: 8 Оценило: 1 человек Средний балл: 2 Оценка: неизвестно Скачать |













































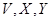 — произвольные пространства над некоторым полем
— произвольные пространства над некоторым полем 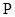 ;
;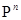 — пространство
— пространство 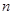 — мерных строк (столбцов) с элементами из поля
— мерных строк (столбцов) с элементами из поля 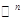 — действительное
— действительное 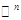 — комплексное
— комплексное 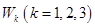 — пространства геометрических векторов (прямой, плоскости, пространства);
— пространства геометрических векторов (прямой, плоскости, пространства);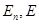 — евклидовы пространства (с указанием размерности или без него);
— евклидовы пространства (с указанием размерности или без него);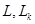 — подпространства данного пространства (
— подпространства данного пространства (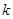 — индекс, не связанный с размерностью);
— индекс, не связанный с размерностью);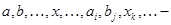 векторы рассматриваемого пространства;
векторы рассматриваемого пространства; 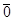 — нулевой вектор;
— нулевой вектор;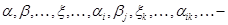 скаляры из данного поля,
скаляры из данного поля,  — нуль этого поля;
— нуль этого поля;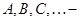 линейные операторы, в отдельных случаях – матрицы;
линейные операторы, в отдельных случаях – матрицы;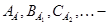 матрицы линейных операторов в базисах соответственно
матрицы линейных операторов в базисах соответственно 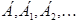 ;
;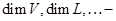 размерности пространств
размерности пространств 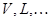 ;
;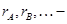 ранги операторов (матриц)
ранги операторов (матриц) 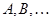 ;
;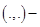 скалярное произведение в данном пространстве;
скалярное произведение в данном пространстве;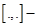 векторное произведение в данном пространстве
векторное произведение в данном пространстве 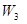 .
.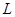 векторов пространства
векторов пространства 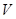 над полем
над полем 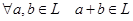 ,
,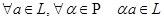 .
.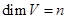 , а
, а 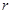 условий специального вида, то есть основания ожидать, что
условий специального вида, то есть основания ожидать, что 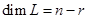 .
.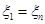 , поэтому
, поэтому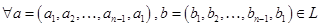
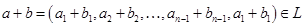 ,
,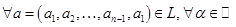
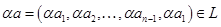 .
.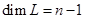 . Для этого рассмотрим векторы стандартного базиса
. Для этого рассмотрим векторы стандартного базиса 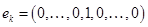
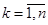 . Векторы
. Векторы 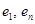 не принадлежат
не принадлежат 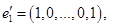
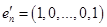 . Рассмотрим систему векторов
. Рассмотрим систему векторов 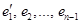 . Она образует базис
. Она образует базис 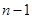 , то и
, то и 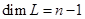 . Итак, наше предположение оказалось верным.
. Итак, наше предположение оказалось верным.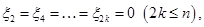 поэтому следует ожидать, что
поэтому следует ожидать, что 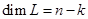 , где
, где 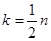 , если
, если 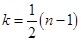 , если
, если 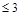 (
(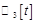 ).
).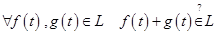 .
.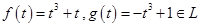 , тогда
, тогда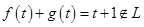 ,
,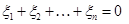 .
.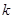 . Однако, замена на векторах
. Однако, замена на векторах 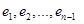 последнего нуля числом (-1) дает нам векторы из
последнего нуля числом (-1) дает нам векторы из 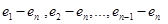
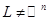 и, следовательно,
и, следовательно, 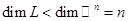 .
.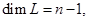
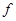 — неотрицательная квадратичная форма от
— неотрицательная квадратичная форма от 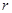 . Доказать, что все решения уравнения
. Доказать, что все решения уравнения 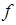 =0 образуют
=0 образуют 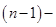 мерное линейное подпространство пространства
мерное линейное подпространство пространства 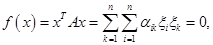
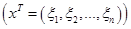 , никак не указывают на способ решения задачи.
, никак не указывают на способ решения задачи.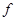 . Нормальный вид такой формы
. Нормальный вид такой формы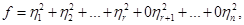 (1)
(1)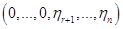 , (2)
, (2)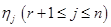 — произвольные числа из
— произвольные числа из 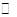 . Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть (
. Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть (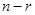 )-мерное подпространство пространства
)-мерное подпространство пространства 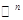 . Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга
. Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга 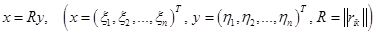 , приводящее форму
, приводящее форму 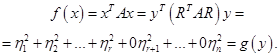
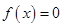 состоит из векторов
состоит из векторов 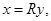 где
где 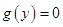 , то есть из векторов
, то есть из векторов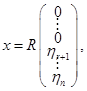
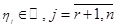 .
.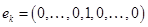 (1 на
(1 на 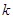 — ой позиции) и докажем, что множество
— ой позиции) и докажем, что множество 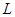 решений уравнения
решений уравнения 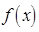 =0 есть линейная оболочка системы векторов
=0 есть линейная оболочка системы векторов 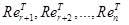
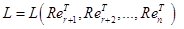 .
.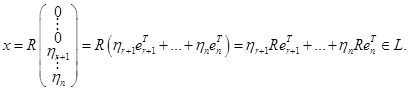
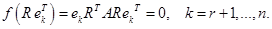
 линейно независима (проверяется непосредственно). Составляем линейную комбинацию
линейно независима (проверяется непосредственно). Составляем линейную комбинацию 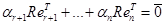 . Получаем
. Получаем 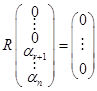 . Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица
. Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица 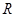 является невырожденной.
является невырожденной.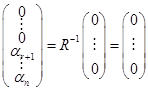 .
.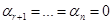 . Тем самым мы показали, что система
. Тем самым мы показали, что система 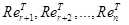 является линейно независимой. Следовательно,
является линейно независимой. Следовательно, 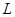 — линейное пространство (по построению) и его размерность
— линейное пространство (по построению) и его размерность 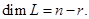
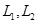 — данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление
— данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление 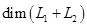 не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств
не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств 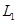 и
и 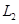 .
. 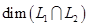 находится по формуле
находится по формуле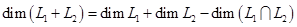 . (3)
. (3)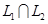 . В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй — с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).
. В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй — с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).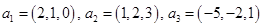 и
и 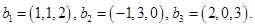
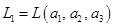 ,
, 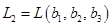 . Будем считать, что координаты векторов заданы в единичном базисе
. Будем считать, что координаты векторов заданы в единичном базисе 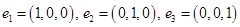 .
.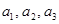 ,
, 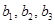 . Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.
. Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.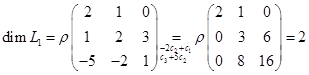 . Базис
. Базис 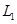 составляют
составляют 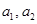 .
.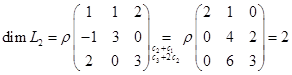 . Базис
. Базис 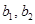 .
.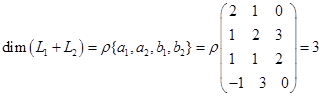 .
.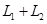 составляют
составляют 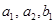 . По формуле (3) получаем
. По формуле (3) получаем 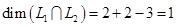 . Базис пересечения будем искать из условия
. Базис пересечения будем искать из условия 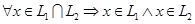 . Значит,
. Значит, 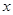 представим в виде
представим в виде 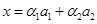 и
и 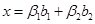 . Приравниваем правые части
. Приравниваем правые части 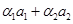
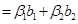 . Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда
. Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда 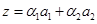
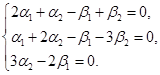
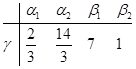
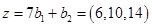 образует базис
образует базис 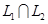 .
.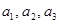 ,
, 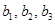 и перебрасываем наверх сначала векторы
и перебрасываем наверх сначала векторы 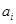 , пока это возможно (квадратиками выделены разрешающие элементы). Векторы
, пока это возможно (квадратиками выделены разрешающие элементы). Векторы 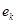 , переходящие налево, не пишем и их координаты не вычисляем.
, переходящие налево, не пишем и их координаты не вычисляем.














