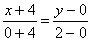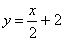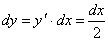- Работа вектора вдоль кривой
- Контакты
- Геометрические и физические приложения
- Примеры решений задач по теории поля
- Примеры: базовые понятия теории поля
- Поток поля через поверхность
- Циркуляция векторного поля
- Работа векторного поля
- Типовой расчет по теории поля
- Помощь с решением заданий
- Найти работу вектора вдоль отрезка винтовой линии
- Контакты
- Найти работу вектора вдоль отрезка винтовой линии
- Решение
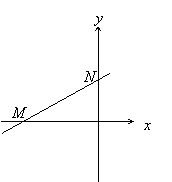
- Построим рисунок.
- 💡 Видео
Видео:Демидович №4452.2: работа поля вдоль отрезкаСкачать

Работа вектора вдоль кривой
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Видео:Демидович №4452: работа поля вдоль винтовой линииСкачать

Геометрические и физические приложения
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
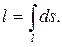
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
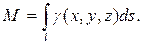
Пример 6.
Найти массу кривой с линейной плотностью 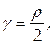
Используем формулу (40) с учетом того, что кривая задана в полярных координатах:
3) Моменты кривой l:
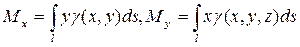
— статические моменты плоской кривой l относительно осей Ох и Оу;
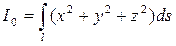
— момент инерции пространственной кривой относительно начала координат;
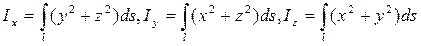
— моменты инерции кривой относительно координатных осей.
4) Координаты центра масс кривой вычисляются по формулам
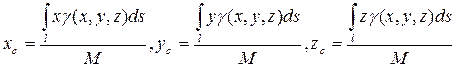
5) Работа силы 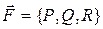
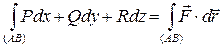
Пример 7.
Вычислить работу векторного поля 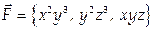
Найдем канонические и параметрические уравнения прямой АВ:
6) Площадь криволинейной поверхности, уравнение которой
z = f(x, y), можно найти в виде:
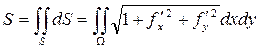
(Ω – проекция S на плоскость Оху).
7) Масса поверхности
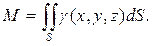
Пример 8.
Найти массу поверхности 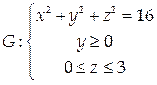
На рассматриваемой поверхности
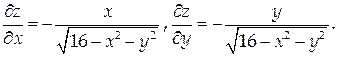
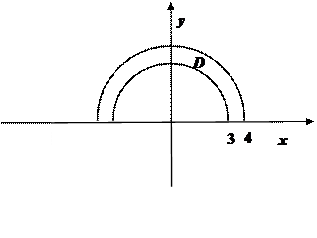
Проекцией D этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.
Применяя формулу (47) и переходя к полярным координатам, получим:
8) Моменты поверхности:
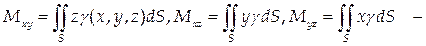
— моменты инерции поверхности относительно координатных осей;
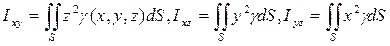
— моменты инерции поверхности относительно координатных плоскостей;
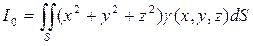
— момент инерции поверхности относительно начала координат.
9) Координаты центра масс поверхности:
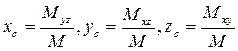
III. Теория поля
Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярноеили векторное).
Если в некоторой области задано скалярное поле U(x,y,z), то вектор
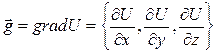
называется градиентомвеличины U в соответствующей точке.
Пусть дано векторное поле 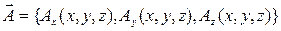
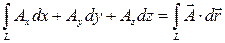
называется линейным интегралом от вектора 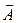
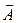
Пример 9.
Вычислить циркуляцию векторного поля 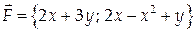
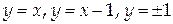
Воспользуемся формулой Грина:
Ротором или вектором вихрявекторного поля A = , где Ax, Ay, Az – функции от x, y, z, называется вектор, определяемый следующим образом:
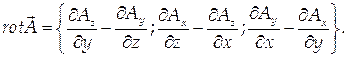
Рассмотрим векторное поле А(М), определенное в пространственной области G, ориентированную гладкую поверхность S 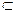
Поверхностный интеграл 1-го рода
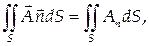
где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.
Пример 10.
Найти поток векторного поля 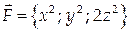
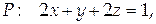
Проекцией данной поверхности на координатную плоскость Оху является треугольник с вершинами в точках А(0;0), В(0;1), С(½; 0). Найдем координаты единичной нормали к плоскости:
Вычислим соответствующий поверхностный интеграл (формула (56)):
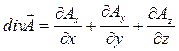
Пример 11.
Найти дивергенцию и ротор векторного поля 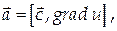
Найдем координаты вектора а:
Векторное поле A = называется потенциальным, если вектор А является градиентом некоторой скалярной функции u = u(x, y, z):
A = grad u = 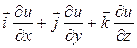
При этом функция и называется потенциалом данного векторного поля.
Пример 12.
Проверить, является ли векторное поле
потенциальным, и в случае положительного ответа найти потенциал и, считая, что в начале координат он равен нулю.
Поле является потенциальным, если выполнены следующие условия:
Следовательно, поле 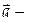
Векторное поле A = называется соленоидальным в области D, если в каждой точке этой области
Видео:Работа векторного поляСкачать

Примеры решений задач по теории поля
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Видео:Векторные линии векторного поляСкачать

Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline=(3x-y) overline+(6z+5x) overline $
Задача 4. Вычислить потенциальную функцию векторного поля
Видео:Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).Скачать

Поток поля через поверхность
Видео:Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать

Циркуляция векторного поля
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ overline = (3x-1) overline+ (y-x+z)overline +4z overline , $$ $L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Видео:Работа векторного поляСкачать

Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline = xz overline -overline +y overline $ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Видео:Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline = z overline+ (x+y)overline +y overline , quad (p): 2x+y+2z=2. $$
Видео:Математический анализ, 48 урок, Криволинейные интегралы второго родаСкачать

Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.
Видео:Разложение вектора по базису. 9 класс.Скачать

Найти работу вектора вдоль отрезка винтовой линии
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
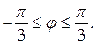
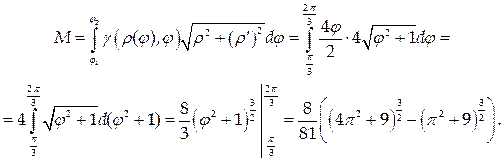
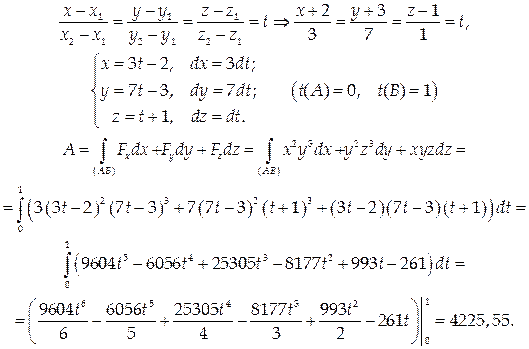

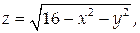
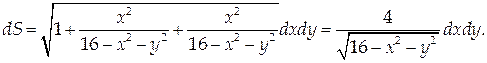
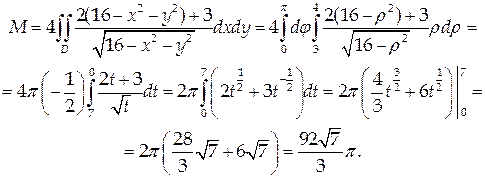
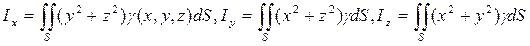

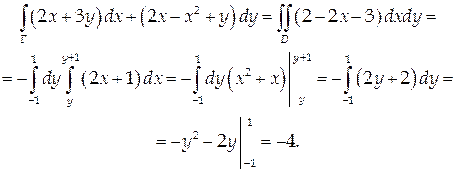
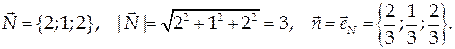
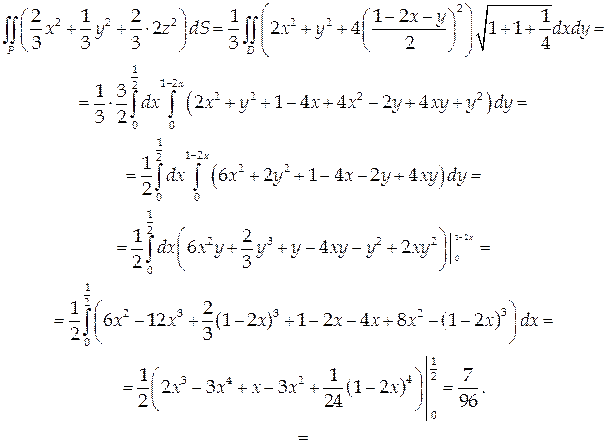
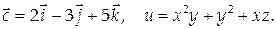
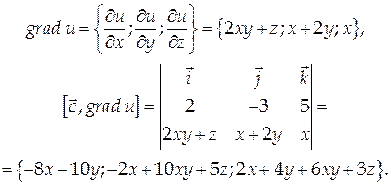
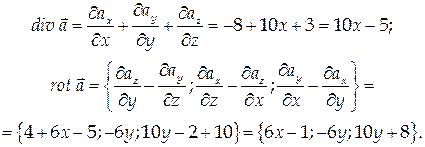
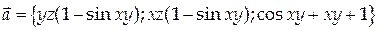
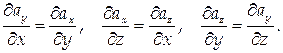
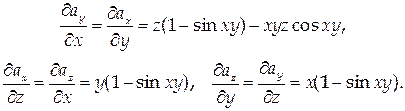
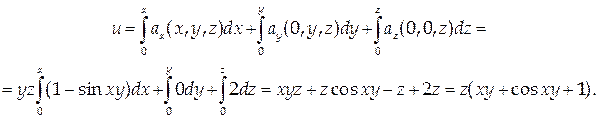

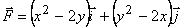 L – отрезок MN, M(-4, 0), N(0, 2).
L – отрезок MN, M(-4, 0), N(0, 2).