Пример №1 . Даны векторы ε1(2;1;3), ε2(3;-2;1), ε3(1;-3;-4), X(7;0;7). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора X в этом базисе.
Решение. Данная задача состоит из двух частей. Сначала необходимо проверить, образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
| E = |
|
∆ = 2*((-2)*(-4) — (-3)*1) — 3*(1*(-4) — (-3)*3) + 1*(1*1 — (-2)*3) = 14
Определитель матрицы равен ∆ =14
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1α2α3, что имеет место равенство:
X = ⓫ε1 + ⓬ε2 + ⓭ε3
Запишем данное равенство в координатной форме:
(7;0;7) = α(2;1;3) + α(3;-2;1) + α(1;-3;-4)
Используя свойства векторов, получим следующее равенство:
(7;0;7) = (2α1;1α1;3α1😉 + (3α2;-2α2;1α2😉 + (1α3;-3α3;-4α3😉
(7;0;7) = (2α1 + 3α2 + 1α3;1α1 -2α2 -3α3;3α1 + 1α2 -4α3)
По свойству равенства векторов имеем:
2α1 + 3α2 + 1α3 = 7
1α1 -2α2 -3α3 = 0
3α1 + 1α2 -4α3 = 7
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:
| X = |
|
X = 2ε1 + ε2
В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
Пример №2 . В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
a1=(1;5;3), a2=(2;1;-1), a3=(4;2;1), a4=(17;13;4).
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

5.1.6. Примеры решения задач по теме «Линейные операторы и квадратичные формы»
Пусть Е1, Е2, Е3, Е4 – базис в векторном пространстве. Разложить вектор
Выпишите матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе. Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.
Выпишем матрицу перехода от старого базиса к новому, столбцами которой являются координаты новых базисных векторов в старом базисе:

Строки этой матрицы являются коэффициентами в формулах преобразования старых координат через новые.
Координаты вектора Х в старом базисе: Х = (1; 2; -1; 3). Пусть в новом базисе он имеет координаты: X = (X, Y, Z, T). Тогда, используя матрицу Т, найдем связь между старыми и новыми координатами:

Следовательно, в новом базисе Х = (-1; 3; -4; 3).
Найти матрицу А’ оператора А:
Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому.
Искомая матрица А’ = T-1 A T, где Т – матрица перехода из старого базиса к новому. Составим матрицу Т :



Ответ: 
Найти собственные числа и собственные векторы линейного оператора, заданного матрицей

Для определения собственных чисел составьте характеристическое уравнение:
Координаты собственных векторов RI = (Xi, Yi) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке LI.
Составим характеристическое уравнение:
Найдем собственные векторы:
1) для L = -2 координаты собственного вектора R1 = (X1, Y1) должны удовлетворять системе уравнений, коэффициенты которых получены из элементов строк определителя, стоящего в левой части характеристического уравнения, при подстановке L = -2:
Если Х1 = 1, то У1 = -1, и R1= (1; -1). Остальные собственные векторы коллинеарны вектору (1; -1), и общий вид собственного вектора, соответствующего L = -2: R1 = С1(1; -1), где С1 – произвольная постоянная.
2) для L = 6 координаты собственного вектора R2 (X2; Y2) удовлетворяют системе:
Пусть Х2 = 3, тогда У2 = 5, и R2 = (3; 5). Соответственно общий вид второго собственного вектора: R2 = С2(3; 5).
Ответ: собственные числа L1 = -2, L2 = 6; собственные векторы R1 = С1(1; -1),
В пространстве 3-мерных векторов задан оператор
Где I – базисный вектор декартовой системы координат.
Выяснить геометрический смысл этого оператора.
Множитель Xi – скалярное произведение, то есть число, поэтому вектор (Xi)I коллинеарен оси Ох.
Оператор А переводит произвольно направленный вектор Х в вектор
KI, коллинеарный оси Ох, поскольку первый множитель – скалярное произведение, то есть число. Из определения скалярного произведения следует, что
Следовательно, А – оператор проектирования на ось Ох.
Оператор осуществляет проектирование вектора Х на ось Ох;
Привести матрицу А линейного оператора к диагональному виду и найти соответствующий базис, если
Найдите собственные числа и собственные векторы матрицы линейного оператора, задайте базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид, и составьте матрицу перехода к новому базису.
Найдем собственные векторы, соответствующие полученным собственным числам.
Подставим в строки определителя L = 2 и найдем связь между координатами собственного вектора R2 = (X2, Y2, Z2):
Та же зависимость получается для координат третьего собственного вектора R3 = (X3, Y3, Z3). Выберем значения двух координат каждого из этих векторов так, чтобы R2 и R3 были линейно независимы.
Пусть Х2 = 1, У2 = 0, тогда Z2 = -3, и R2 = (1; 0; -3).
Получен базис из линейно независимых собственных векторов R1, R2, R3 , в котором матрица оператора примет диагональный вид.
Составим матрицу перехода к новому базису:
Найдем матрицу, обратную к Т:

Тогда в базисе из собственных векторов матрица оператора
Ответ: в базисе (1; 1; 1), (1; 0; -3), (0; 1; 3) матрица оператора
Линейный оператор А задан в некотором базисе матрицей
Найти собственные числа и собственные векторы оператора А-1 – оператора, обратного к А.
Собственные числа обратного оператора являются обратными к собственным числам данного оператора, а их собственные векторы одинаковы.
Характеристическое уравнение для А:
Найдем матрицу обратного оператора:

Соответствующее характеристическое уравнение:
Составить матрицу квадратичной формы 3Х2 – 10Ху + 8У2 и найти ее собственные числа.
Матрица квадратичной формы А11Х2 + 2А12Ху + А22У2 является
Симметрической (Aij = Aji) и имеет вид:
В нашей задаче А11 = 3, А12 = -5, А22 = 8. Следовательно,
Составим характеристическое уравнение, корнями которого являются собственные числа:
Ответ: матрица квадратичной формы 
Собственные числа
Найти базис, в котором квадратичная форма 2Х2 + 4Ху + 5У2 будет иметь канонический вид, и указать этот вид.
Канонический вид квадратичной формы:
1) во-первых, не содержит произведения Ху;
2) во-вторых, коэффициенты при Х2 и У2 равны собственным числам матрицы квадратичной формы.
Базис, в котором квадратичная форма имеет канонический вид, состоит из нормированных собственных векторов матрицы квадратичной формы.
Матрица квадратичной формы
Собственные числа: L1 = 1, L2 = 6.
Для L1 = 1 координаты вектора R1 = <X1, Y1> определяются уравнением
Х1 + 2У1 = 0, Х1 = -2У1. Если У1 = 1, то Х1 = -2, и R1 = C. Найдем значение С из условия, что вектор R1 нормирован, то есть его длина равна 1:
Итак, базис имеет вид:
И в этом базисе квадратичная форма примет вид: L1Х2 + L2У2, то есть Х2 + 6У2.
Ответ: в базисе 
Указать преобразование координат, приводящее квадратичную форму
8Х2 – 12Ху + 17У2 к каноническому виду.
Матрица преобразования координат имеет вид:
Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы.
Найдем базис из нормированных собственных векторов.
Составим матрицу перехода к новому базису, столбцами которой будут координаты новых базисных векторов R1, R2 в старом базисе:
Строки этой матрицы определяют коэффициенты уравнений, выражающих старые координаты через новые:
Где Х, У – координаты в старом базисе, а Х’, Y’ – в новом.
Таким образом, найдено искомое преобразование.
Ответ: 
Привести к каноническому виду квадратичную форму 5Х2 – 12Ху.
Матрица преобразования координат имеет вид:
Где R1 = (X1, Y1) и R2 = (X2, Y2) – нормированные собственные векторы. В новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.
Матрица перехода к базису из собственных векторов:
Подставим найденные выражения в квадратичную форму:
Как и следовало ожидать, в новом базисе квадратичная форма имеет канонический вид, причем коэффициенты при Х2 и У2 совпадают с собственными числами матрицы квадратичной формы.
Найти преобразование координат, приводящее квадратичную форму
X2 + Y2 + 5Z2 – 6Xy + 2Xz – 2Yz к каноническому виду.
Матрица преобразования координат:
Для заданной квадратичной формы
Составим и решим характеристическое уравнение:
(Мы не останавливаемся подробно на способах решения уравнений высших порядков. В данном случае, например, один из корней был найден перебором делителей свободного члена, а затем левая часть разложена на множители.)
Найдем нормированные собственные векторы:
Матрица перехода к новому базису:
Задает преобразование координат:
Заметим, что в новых координатах квадратичная форма примет вид:
Где коэффициенты являются собственными числами, стоящими в той же последовательности, что и соответствующие собственные векторы в матрице Т.
Ответ:
Видео:Решение, показать, что векторы e1, е2, е3 образуют базис и найти в нем координаты вектора а пример 1Скачать

Доказать что векторы е1 е2 е3 образуют базис и найти координаты вектора Х в этом базисе.
Х=(-4,-2,5)
е1=(1,-1,1)
е2=(-3,0,2)
е3=(1,-1,2)
Даны векторы e1(1;-1;1), e2(-3;0;2), e3(1;-1;2), X(-4;-2;5). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора X в этом базисе.
Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
Определитель матрицы равен ∆ =-3
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство:
X = α1e1 + α2e2 + α3e3
Запишем данное равенство в координатной форме:
Используя свойства векторов, получим следующее равенство:
(-4;-2;5) = (1α1;-1α1;1α1;) + (-3α2;0α2;2α2;) + (1α3;-1α3;2α3;)
(-4;-2;5) = (1α1 -3α2 + 1α3;-1α1 + 0α2 -1α3;1α1 + 2α2 + 2α3)
По свойству равенства векторов имеем:
1α1 -3α2 + 1α3 = -4
-1α1 + 0α2 -1α3 = -2
1α1 + 2α2 + 2α3 = 5
Решаем полученную систему уравнений методом Крамера.
💡 Видео
Координаты в новом базисеСкачать

Найдите разложение вектора по векторам (базису)Скачать

Как разложить вектор по базису - bezbotvyСкачать

Решение, убедиться что векторы e1, е2, е3 образуют базис и найти в нем координаты вектора а пример 9Скачать

Базис и матрица перехода. Координаты вектора в разных базисах.Скачать

Решение, показать, что векторы e1, е2, е3 образуют базис и найти в нем координаты вектора а пример 2Скачать

Базис. Разложение вектора по базису.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Координаты вектора. 9 класс.Скачать

Образуют ли данные векторы базисСкачать

9 класс, 2 урок, Координаты вектораСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Разложение вектора по базису. 9 класс.Скачать

Координаты точки и координаты вектора 1.Скачать

Координаты вектора в пространстве. 11 класс.Скачать

Матрица переходаСкачать
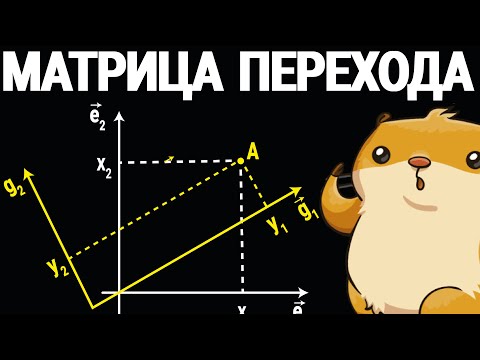
Замена базиса. ТемаСкачать











































