Параллельные прямые не пересекаются (Что такое суждение)
Суждение (высказывание) – это форма мышления, в которой что-либо утверждается или отрицается. Например: Все сосны являются деревьями, Некоторые люди – это спортсмены, Ни один кит – не рыба, Некоторые животные не являются хищниками. Рассмотрим несколько важных свойств суждения, которые в то же время отличают его от понятия.
1. Любое суждение состоит из понятий, связанных между собой. Например, если связать понятия карась и рыба, то могут получиться суждения Все караси являются рыбами, Некоторые рыбы являются карасями.
2. Любое суждение выражается в форме предложения (как мы помним, понятие выражается словом или словосочетанием). Однако не всякое предложение может выражать суждение. Как известно, предложения бывают повествовательными, вопросительными и восклицательными. В вопросительных и восклицательных предложениях ничего не утверждается и не отрицается, поэтому они не могут выражать собой суждение. Повествовательное предложение, наоборот, всегда что-либо утверждает или отрицает, в силу чего суждение выражается в форме повествовательного предложения.
Тем не менее есть такие вопросительные и восклицательные предложения, которые только по форме являются вопросами и восклицаниями, а по смыслу что-то утверждают или отрицают. Они называются риторическими. Например, известное высказывание И какой же русский не любит быстрой езды? представляет собой риторическое вопросительное предложение (риторический вопрос), так как в нем в форме вопроса утверждается, что всякий русский любит быструю езду. В подобном вопросе заключено суждение. То же самое можно сказать о риторических восклицаниях. Например, в высказывании Попробуй найти черную кошку в темной комнате, если ее там нет! в форме восклицательного предложения утверждается мысль о невозможности предложенного действия, в силу чего данное восклицание выражает собой суждение. Понятно, что не риторический, а настоящий вопрос (например: Как тебя зовут?) не выражает суждение, точно так же, как не выражает его настоящее, а не риторическое восклицание (например: Прощай, свободная стихия!).
Чтобы лучше уяснить, что такое суждение, рассмотрим несколько примеров.
• Неужели ты не знал, что Земля вращается вокруг Солнца? (Риторический вопрос – является суждением).
• Прощай, немытая Россия! (Восклицание – суждением не является).
• Кто написал философский трактат «Критика чистого разума»? (Вопрос – суждением не является).
• Логика появилась примерно в V в. до н. э. в Древней Греции. (Повествование – является суждением).
• Первый президент Америки. (Понятие – суждением не является).
• Разворачивайтесь в марше! (Восклицание – суждением не является).
• Мы все учились понемногу… (Повествование – является суждением).
• Попробуй-ка двигаться со скоростью света! (Риторическое восклицание – является суждением).
• Средняя школа № 469 г. Москвы. (Понятие – суждением не является).
• Как тебе только не стыдно? (Риторический вопрос – является суждением).
• Каким образом решается знаменитая задача о квадратуре круга? (Вопрос – суждением не является).
• Общая теория относительности А. Эйнштейна. (Понятие – суждением не является).
• Почему нельзя делить на ноль? (Вопрос – суждением не является).
• Бескрайние просторы Вселенной. (Понятие – суждением не является).
• Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. (Повествование – является суждением).
3. Любое суждение является истинным или ложным.
Если суждение соответствует действительности, оно истинное, а если не соответствует – ложное. Например, суждение Все розы – это цветы является истинным, а суждение Все мухи – это птицы – ложным. Надо отметить, что понятия, в отличие от суждений, не могут быть истинными или ложными. Невозможно, например, утверждать, что понятие школа – истинное, а понятие институт – ложное, понятие звезда – истинное, а понятие планета – ложное и т. п. Но разве понятия Змей Горыныч, Кощей Бессмертный, вечный двигатель не ложные? Нет, эти понятия являются нулевыми (пустыми), но не истинными и не ложными. Вспомним, понятие – это форма мышления, которая обозначает какой-либо объект, и именно поэтому не может быть истинным или ложным. Истинность или ложность – это всегда характеристика какого-то высказывания, утверждения или отрицания, поэтому она применима только к суждениям, а не к понятиям.
4. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом.
Как видим, суждение – это более сложная форма мышления по сравнению с понятием. Неудивительно поэтому, что суждение имеет определенную структуру, в которой можно выделить четыре части: субъект, предикат, связка и квантор.
Субъект (обозначается латинской буквой S) – это то, о чем идет речь в суждении. Например, в суждении Все учебники являются книгами речь идет об учебниках, поэтому субъектом данного суждения выступает понятие учебники.
Предикат (обозначается латинской буквой Р) – это то, что говорится о субъекте. Например, в том же суждении Все учебники являются книгами о субъекте (об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие книги.
Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова есть, является, это и т. п.
Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, ни один и т. п.
Рассмотрим суждение Некоторые люди являются спортсменами. В нем субъектом выступает понятие люди, предикатом – понятие спортсмены, роль связки играет слово являются, а слово некоторые представляет собой квантор. Если в каком-то суждении отсутствует связка или квантор, то они все равно подразумеваются. Например, в суждении Тигры – это хищники квантор отсутствует, но он подразумевается – это слово все. С помощью условных обозначений субъекта и предиката можно отбросить содержание суждения и оставить только его логическую форму. Например, если у суждения Все прямоугольники – это геометрические фигуры отбросить содержание и оставить форму то получится: Все S есть Р. Логическая форма суждения Некоторые животные не являются млекопитающими есть Некоторые S не есть Р.
Субъект и предикат любого суждения всегда представляют собой какие-либо понятия, которые, как мы уже знаем, могут находиться в различных отношениях между собой. Между субъектом и предикатом суждения могут быть следующие логические отношения: равнозначности, пересечения, подчинения и несовместимости.
Отношение равнозначности предполагает, что субъект и предикат представляют собой равнозначные понятия. В суждении Все квадраты – это равносторонние прямоугольники субъект квадраты и предикат равносторонние прямоугольники находятся в отношении равнозначности, потому что квадрат – это обязательно равносторонний прямоугольник, а равносторонний прямоугольник – это обязательно квадрат (рис. 17).
Отношения равнозначности субъекта и предиката иллюстрируют примеры ниже:
Антарктида представляет собой ледовый материк (равнозначность).
Д. И. Менделеев – создатель Периодической системы химических элементов (равнозначность).
Отношение пересечения показывает, что субъект и предикат суждения являются пересекающимися понятиями. В суждении Некоторые писатели – это американцы субъект писатели и предикат американцы находятся в отношении пересечения (так как писатель может быть американцем и может им не быть, и американец может быть писателем, но также может им не быть) (рис. 18).
Отношением пересечения связаны субъект и предикат следующих суждений:
Некоторые русские писатели – это всемирно известные люди.
Некоторые грибы – несъедобные объекты.
Некоторые ученые – древние греки.
При отношении подчинения субъект и предикат суждения соотносятся как видовое и родовое понятия. В суждении Все тигры – это хищники субъект тигры и предикат хищники находятся в отношении подчинения, потому что тигр – это обязательно хищник, но хищник не обязательно тигр. Так же в суждении Некоторые хищники являются тиграми субъект хищники и предикат тигры находятся в отношении подчинения, будучи родовым и видовым понятиями.
Отношение подчинения хорошо иллюстрируют следующие суждения:
• Все бактерии являются живыми организмами.
• Солнце – это одна из звезд.
• Не все спортсмены являются олимпийскими чемпионами.
Отметим, в случае подчинения между субъектом и предикатом суждения возможны два варианта отношений: объем субъекта полностью включается в объем предиката (рис. 19), или наоборот (рис. 20).
Отношение несовместимости означает, что субъект и предикат суждения являются несовместимыми (соподчиненными) понятиями. В суждении Все планеты не являются звездами субъект планеты и предикат звезды находятся в отношении несовместимости, так как ни одна планета не может быть звездой, и ни одна звезда не может быть планетой (рис. 21).
В приведенных ниже суждениях субъект и предикат находятся в отношении несовместимости:
Параллельные прямые не пересекаются (несовместимость).
Учебники не могут быть развлекательными книгами (несовместимость).
Чтобы установить, в каком отношении находятся субъект и предикат того или иного суждения, надо сначала установить, какое понятие данного суждения является субъектом, а какое предикатом. Для примера определим отношение между субъектом и предикатом в суждении Некоторые военнослужащие являются россиянами.
Сначала находим субъект суждения, – это понятие военнослужащие, затем устанавливаем его предикат, – это понятие россияне. Понятия военнослужащие и россияне находятся в отношении пересечения (военнослужащий может быть россиянином и может им не быть; и россиянин может как быть, так и не быть военнослужащим). Следовательно, в указанном суждении субъект и предикат пересекаются.
Точно так же в суждении Все планеты – это небесные тела субъект и предикат находятся в отношении подчинения, а в суждении Ни один кит не является рыбой субъект и предикат несовместимы.
Как правило, все суждения подразделяют на три вида:
Атрибутивные суждения (от лат. attributum – «неотъемлемый признак») – это суждения, в которых предикат представляет собой какой-либо существенный, неотъемлемый признак субъекта. Например, суждение Все воробьи – это птицы – атрибутивное, потому что его предикат является неотъемлемым признаком субъекта, ведь быть птицей – это главный признак воробья, его атрибут, без которого он не будет самим собой (если некий объект не птица, то он обязательно и не воробей).
Надо отметить, что в атрибутивном суждении не обязательно предикат является атрибутом субъекта, может быть и наоборот – субъект представляет собой атрибут предиката. Например, в суждении Некоторые птицы – это воробьи (как видим, по сравнению с вышеприведенным примером, субъект и предикат поменялись местами) субъект является неотъемлемым признаком (атрибутом) предиката. Однако эти суждения всегда можно формально изменить таким образом, что предикат станет атрибутом субъекта. Поэтому атрибутивными обычно называются те суждения, в которых предикат является атрибутом субъекта.
Экзистенциальные суждения (от лат. existentia – «существование») – это суждения, в которых предикат указывает на существование или несуществование субъекта. Например, суждение Вечных двигателей не бывает является экзистенциальным, так как его предикат не бывает свидетельствует о несуществовании субъекта (вернее – предмета, который обозначен субъектом).
Релятивные суждения (от лат. relativus – «относительный») – это суждения, в которых предикат выражает собой какое-то отношение к субъекту. Например, суждение Москва основана раньше Санкт-Петербурга является релятивным, потому что его предикат основана раньше Санкт-Петербурга указывает на временное (возрастное) отношение одного города и соответствующего понятия к другому городу и соответствующему понятию, представляющему собой субъект суждения.
В мышлении и языке большую часть составляют атрибутивные суждения. Они встречаются чаще, чем экзистенциальные и релятивные. Кроме того, последние, в принципе, можно представить как атрибутивные. Вернемся к экзистенциальному суждению Вечных двигателей не бывает. Его предикат (не быть или не существовать) вполне можно рассматривать как атрибут субъекта (вечные двигатели), ведь не существовать – это действительно неотъемлемый признак вечных двигателей, следовательно, данное суждение возможно расценивать как атрибутивное.
Теперь обратимся к релятивному суждению Москва основана раньше Санкт-Петербурга, предикат которого (быть основанным раньше Санкт-Петербурга) вполне можно рассматривать как атрибут субъекта (Москва), ведь быть старше Санкт-Петербурга (ранее основанным городом) – это действительно неотъемлемый признак Москвы. Таким образом, это суждение также возможно охарактеризовать как атрибутивное.
Все и некоторые, есть и не есть (Виды простых суждений)
Если в суждении присутствуют один субъект и один предикат, то оно является простым. Все простые суждения по объему субъекта и качеству связки делятся на четыре вида. Объем субъекта может быть общим (всё) и частным (некоторые), а связка может быть утвердительной (есть) и отрицательной (не есть).
На основе объема субъекта и качества связки можно выделить только четыре комбинации, которыми исчерпываются все виды простых суждений: все – есть, некоторые – есть, все – не есть, некоторые – не есть. Каждый из этих видов имеет свое название и условное обозначение.
Общеутвердительные суждения (обозначаются латинской буквой А) – это суждения с общим объемом субъекта и утвердительной связкой, т. е. одновременно общие и утвердительные: Все S есть Р. Например: Все школьники являются учащимися.
Частноутвердительные суждения (обозначаются латинской буквой I) – это суждения с частным объемом субъекта и утвердительной связкой, т. е. одновременно частные и утвердительные: Некоторые S есть Р. Например: Некоторые животные являются хищниками.
Общеотрицательные суждения (обозначаются латинской буквой Е) – это суждения с общим объемом субъекта и отрицательной связкой, т. е. одновременно общие и отрицательные: Все S не есть Р (или Ни одно S не есть Р). Например: Все планеты не являются звездами, Ни одна планета не является звездой.
Частноотрицательные суждения (обозначаются латинской буквой О) – это суждения с частным объемом субъекта и отрицательной связкой, т. е. одновременно частные и отрицательные: Некоторые S не есть Р. Например: Некоторые грибы не являются съедобными.
Далее следует ответить на вопрос, к каким суждениям – общим или частным – следует относить суждения с единичным объемом субъекта (т. е. те суждения, в которых субъект представляет собой единичное понятие), например: Солнце – это небесное тело, Москва основана в 1147 году, Антарктида – это один из материков Земли. Суждение является общим, если речь в нем идет обо всем объеме субъекта, и частным, если речь идет о части объема субъекта. В суждениях с единичным объемом субъекта речь идет обо всем объеме субъекта (в приведенных примерах – обо всем Солнце, обо всей Москве, обо всей Антарктиде). Таким образом, суждения, в которых субъект является единичным понятием, считаются общими (общеутвердительными или общеотрицательными). Так, три приведенных выше суждения – общеутвердительные, а суждение Известный итальянский ученый эпохи Возрождения Галилео Галилей не является автором теории электромагнитного поля – общеотрицательное.
В дальнейшем будем говорить о видах простых суждений, не употребляя их длинных названий, с помощью условных обозначений – латинских букв А, I, Е, О. Эти буквы, взятые из двух латинских слов: affirmo – «утверждать» и nego – «отрицать», были предложены в качестве обозначения видов простых суждений еще в Средние века.
Важно отметить, что в каждом из видов простых суждений субъект и предикат находятся в определенных отношениях. Так, общий объем субъекта и утвердительная связка суждений вида А приводят к тому, что в них субъект и предикат могут находиться в отношениях равнозначности или подчинения (других отношений между субъектом и предикатом в суждениях вида А быть не может). Например, в суждении Все квадраты (S) – это равносторонние прямоугольники (Р) субъект и предикат находятся в отношении равнозначности, а в суждении Все киты (S) – это млекопитающие животные (Р) – в отношении подчинения.
Частный объем субъекта и утвердительная связка суждений вида I обусловливают то, что в них субъект и предикат могут находиться в отношениях пересечения или подчинения (но не в других). Например, в суждении Некоторые спортсмены (S) – это негры (Р) субъект и предикат находятся в отношении пересечения, а в суждении Некоторые деревья (S) – это сосны (Р) – в отношении подчинения.
Общий объем субъекта и отрицательная связка суждений вида Е приводят к тому, что в них субъект и предикат находятся только в отношении несовместимости. Например, субъект и предикат несовместимы в суждениях Все киты (S) – это не рыбы (Р), Все планеты (S) не являются звездами (Р), Все треугольники (S) – это не квадраты (Р).
Частный объем субъекта и отрицательная связка суждений вида О обусловливают то, что в них субъект и предикат, так же как и в суждениях вида I, могут быть только в отношениях пересечения и подчинения. Например, в суждении Некоторые студенты (S) не являются спортсменами (Р) субъект и предикат находятся в отношении пересечения, а в суждении Некоторые геометрические фигуры (S) не являются треугольниками (Р) субъект и предикат находятся в отношении подчинения.
Обо всем или о части (Распределенность терминов в простых суждениях)
Терминами суждения называются его субъект и предикат.
Термин считается распределенным (развернутым, исчерпанным, взятым в полном объеме), если в суждении речь идет обо всех объектах, входящих в объем этого термина. Распределенный термин обозначается знаком «+», а на схемах Эйлера изображается полным кругом (кругом, который не содержит в себе другого круга и не пересекается с другим кругом) (рис. 22).
Термин считается нераспределенным (неразвернутым, неисчерпанным, взятым не в полном объеме), если в суждении речь идет не обо всех объектах, входящих в объем этого термина. Нераспределенный термин обозначается знаком «—», а на схемах Эйлера изображается неполным кругом (кругом, который содержит в себе другой круг (рис. 23а) или пересекается с другим кругом (рис. 23б).
Например, в суждении Все акулы (S) являются хищниками (Р) речь идет обо всех акулах, значит, субъект этого суждения распределен. Однако в данном суждении речь идет не обо всех хищниках, а только о части хищников (именно о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределен. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения схемами Эйлера, увидим, что распределенному термину (субъекту акулы) соответствует полный круг, а нераспределенному (предикату хищники) – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть) (рис. 24).
Распределенность терминов в простых суждениях может быть различной в зависимости от вида суждения и характера отношений между его субъектом и предикатом.
Проще всего устанавливать распределенность терминов в простых суждениях с помощью схем Эйлера. Достаточно уметь определять вид отношений между субъектом и предикатом в предложенном суждении и изображать их круговыми схемами. Далее еще проще – полный круг, как уже говорилось, соответствует распределенному термину, а неполный – нераспределенному. Например, требуется установить распределенность терминов в суждении Некоторые русские писатели – это всемирно известные люди. Сначала найдем в этом суждении субъект и предикат: русские писатели – субъект, всемирно известные люди – предикат. Теперь установим, в каком отношении они находятся. Русский писатель может как быть, так и не быть всемирно известным человеком, и всемирно известный человек может как быть, так и не быть русским писателем, следовательно, субъект и предикат указанного суждения находятся в отношении пересечения. Изобразим это отношение на схеме Эйлера, заштриховав ту часть, о которой идет речь в суждении (рис. 25).
И субъект, и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно, оба термина предложенного суждения нераспределены (S —, Р —).
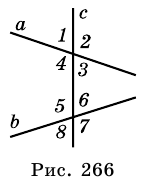
Рассмотрим еще один пример. Надо установить распределенность терминов в суждении Некоторые люди – это спортсмены. Найдя в этом суждении субъект и предикат (люди – субъект, спортсмены – предикат) и установив отношение между ними (подчинение), изобразим его на схеме Эйлера, заштриховав ту часть, о которой идет речь в суждении (рис. 26).
Круг, обозначающий предикат, является полным, а круг, соответствующий субъекту, – неполным (круг предиката как бы вырезает из него какую-то часть). Таким образом, в данном суждении субъект нераспределен, а предикат распределен (S —, Р +).
Все не рыбы не являются карасями (Способы преобразования простых суждений)
Существует три способа преобразования, т. е. изменения формы, простых суждений: обращение, превращение и противопоставление предикату.
Обращение – это преобразование простого суждения, при котором субъект и предикат меняются местами. Например, суждение Все акулы являются рыбами преобразуется путем обращения в суждение Некоторые рыбы являются акулами. Здесь может возникнуть вопрос, почему исходное суждение начинается с квантора все, а новое – с квантора некоторые! Этот вопрос на первый взгляд кажется странным, ведь нельзя же сказать Все рыбы являются акулами, следовательно, единственное, что остается, это Некоторые рыбы являются акулами. Однако в данном случае мы обратились к содержанию суждения и по смыслу поменяли квантор все на квантор некоторые; а логика, как уже говорилось, отвлекается от содержания мышления и занимается только его формой. Поэтому обращение суждения Все акулы являются рыбами можно выполнить формально, не обращаясь к его содержанию (смыслу). Для этого установим распределенность терминов в этом суждении с помощью круговой схемы. Термины суждения, т. е. субъект акулы и предикат рыбы, находятся в данном случае в отношении подчинения (рис. 27).
На круговой схеме видно, что субъект распределен (полный круг), а предикат нераспределен (неполный круг). Вспомним, что термин распределен, когда речь идет обо всех входящих в него предметах, и нераспределен, когда – не обо всех, и автоматически мысленно поставим перед термином акулы квантор все, а перед термином рыбы – квантор некоторые. Делая обращение указанного суждения, т. е. меняя местами его субъект и предикат и начиная новое суждение с термина рыбы, мы опять же автоматически снабжаем его квантором некоторые, не задумываясь о содержании исходного и нового суждений, и получаем безошибочный вариант: Некоторые рыбы являются акулами.
Возможно, все это покажется чрезмерным усложнением элементарной операции, однако далее мы увидим,
Обратим внимание на то, что в рассмотренном выше примере исходное суждение было вида А, а новое – вида I, т. е. операция обращения привела к смене вида простого суждения. При этом, конечно же, поменялась его форма, но не поменялось содержание, ведь в суждениях Все акулы являются рыбами и Некоторые рыбы являются акулами речь идет об одном и том же. Суждение вида А обращается или само в себя, или в суждение вида I. Суждение вида I обращается или само в себя, или в суждение вида А. Суждение вида Е всегда обращается само в себя, а суждение вида О обращению не поддается.
Второй способ преобразования простых суждений, называемый превращением, заключается в том, что у суждения меняется связка: положительная на отрицательную, или наоборот. При этом предикат суждения заменяется противоречащим понятием (т. е. перед предикатом ставится частица НЕ). Например, то же самое суждение, которое мы рассматривали в качестве примера для обращения Все акулы являются рыбами, преобразуется путем превращения в суждение Все акулы не являются не рыбами. Это суждение может показаться странным, ведь обычно так не говорят, хотя на самом деле перед нами более короткая формулировка той мысли, что ни одна акула не может быть таким существом, которое не является рыбой, или что множество всех акул исключается из множества всех существ, которые не являются рыбами. Субъект акулы и предикат не рыбы суждения, получившегося в результате превращения, находятся в отношении несовместимости (рис. 28).
Приведенный пример превращения демонстрирует важную логическую закономерность: любое утверждение равно двойному отрицанию, и наоборот. Как видим, исходное суждение вида А в результате превращения стало суждением вида Е. В отличие от обращения превращение не зависит от характера отношений между субъектом и предикатом простого суждения. Поэтому суждение вида А всегда превращается в суждение вида Е, а суждение вида Е – в суждение вида А. Суждение вида I всегда превращается в суждение вида О, а суждение вида О – в суждение вида I.
Третий способ преобразования простых суждений – противопоставление предикату – состоит в том, что сначала суждение подвергается превращению, а потом обращению. Например, чтобы путем противопоставления предикату преобразовать суждение Все акулы являются рыбами, надо сначала подвергнуть его превращению. Получится: Все акулы не являются не рыбами. Теперь надо совершить обращение с получившимся суждением, т. е. поменять местами его субъект акулы и предикат не рыбы. Чтобы не ошибиться, вновь прибегнем к установлению распределенности терминов с помощью круговой схемы (субъект и предикат в этом суждении находятся в отношении несовместимости) (рис. 29).
На круговой схеме видно, что и субъект, и предикат распределены (и тому, и другому термину соответствует полный круг), следовательно, мы должны сопроводить как субъект, так и предикат квантором все. После этого совершим обращение с суждением Все акулы не являются не рыбами. Получится: Все не рыбы не являются акулами. Суждение звучит непривычно, однако это – более короткая формулировка той мысли, что если какое-то существо не является рыбой, то оно никак не может быть акулой, или что все существа, которые не являются рыбами, автоматически не могут быть и акулами в том числе.
Все три операции преобразования простых суждений проще всего совершать с помощью круговых схем. Для этого надо изобразить кругами Эйлера три термина: субъект, предикат и понятие, противоречащее предикату (не-предикат). Потом следует установить их распределенность, и из получившейся схемы будут вытекать четыре суждения – одно исходное и три результата преобразований. Главное – помнить, что распределенный термин соответствует квантору все, а нераспределенный – квантору некоторые; что соприкасающиеся на схеме Эйлера круги соответствуют связке является, а несоприкасающиеся – связке не является. Например, требуется совершить три операции преобразования с суждением Все учебники являются книгами. Изобразим субъект учебники, предикат книги и не-предикат не книги круговой схемой и установим распределенность этих терминов (рис. 30).
Получившуюся круговую схему можно прочитать четырьмя способами:
• Все учебники являются книгами (исходное суждение).
• Некоторые книги являются учебниками (обращение).
• Все учебники не являются не книгами (превращение).
• Все не книги не являются учебниками (противопоставление предикату).
Рассмотрим еще один пример. Надо преобразовать тремя способами суждение Все планеты не являются звездами. Изобразим кругами Эйлера субъект планеты, предикат звезды и не-предикат не звезды. Обратите внимание на то, что понятия планеты и не звезды находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой, – это не обязательно планета. Установим распределенность этих терминов (рис. 31).
Получившуюся круговую схему можно прочитать четырьмя разными способами:
• Все планеты не являются звездами (исходное суждение).
• Все звезды не являются планетами (обращение).
• Все планеты являются не звездами (превращение).
• Некоторые не звезды являются планетами (противопоставление предикату).
Логический квадрат (Отношения между суждениями)
Простые суждения делятся на сравнимые и несравнимые.
Сравнимые (идентичные по материалу) суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения Все школьники изучают математику, Некоторые школьники не изучают математику являются сравнимыми, так как у них совпадают субъекты и предикаты, а кванторы и связки различаются.
Несравнимые суждения имеют разные субъекты и предикаты. Например, суждения: Все школьники изучают математику, Некоторые спортсмены – это олимпийские чемпионы являются несравнимыми, так как субъекты и предикаты у них не совпадают.
Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.
Совместимыми называются суждения, которые могут быть одновременно истинными. Например, суждения Некоторые люди – это спортсмены, Некоторые люди – это не спортсмены являются одновременно истинными и представляют собой совместимые суждения.
Несовместимыми называются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения Все школьники изучают математику, Некоторые школьники не изучают математику не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).
Совместимые суждения могут находиться в отношениях равнозначности, подчинения или частичного совпадения.
Равнозначность – это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения Москва является древним городом, Столица России является древним городом находятся в отношении равнозначности.
Подчинение – это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения Все растения являются живыми организмами, Все цветы (некоторые растения) являются живыми организмами находятся в отношении подчинения.
Частичное совпадение – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения Некоторые грибы являются съедобными и Некоторые грибы не являются съедобными находятся в отношении частичного совпадения. Необходимо отметить, что в этом отношении находятся только частные суждения – частноутвердительные (I) и частноотрицательные (О).
Несовместимые суждения могут находиться в отношениях противоположности или противоречия.
Противоположность – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения Все люди являются правдивыми и Все люди не являются правдивыми находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные (Д) и общеотрицательные (Е).
Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Вернемся к приведенным выше суждениям и убедимся в этом: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми. Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями Все люди являются правдивыми и Все люди не являются правдивыми есть третий, средний вариант Некоторые люди являются правдивыми, а некоторые не являются таковыми, который, будучи истинным суждением, обусловливает одновременную ложность двух крайних противоположных суждений.
Противоречие – это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объемами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения Все люди являются правдивыми и Некоторые люди не являются правдивыми находятся в отношении противоречия.
Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот, ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы еще вернемся, когда речь пойдет о логических законах противоречия и исключенного третьего.
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан еще средневековыми логиками.
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия.
Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О.
Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – это противоречие.
Суждения Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений (в отличие от понятий) является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так, если суждение вида А является истинным или ложным, то три других (I, Е, О), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида А) тоже являются истинными или ложными.
Например, если суждение вида А: Все тигры – это хищники – истинно, то суждение вида I. Некоторые тигры – это хищники – также истинно (если все тигры – хищники, то и часть из них, т. е. некоторые тигры, – это тоже хищники); суждение вида Е Все тигры – это не хищники – ложно, и суждение вида О: Некоторые тигры – это не хищники – также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Чем дальше в лес, тем больше дров (Виды сложных суждений)
В зависимости от союза, с помощью которого простые суждения соединяются в сложные, выделяется пять видов сложных суждений: конъюнктивные, дизъюнктивные, импликативные, эквивалентные и отрицательные суждения.
Конъюнктивное суждение (конъюнкция) – это сложное суждение с соединительным союзом И, который обозначается в логике условным знаком «?». С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: а ? b (читается «а и b»), где а и b – это два каких-либо простых суждения. Например, сложное суждение: Сверкнула молния, и загремел гром является конъюнкцией (соединением) двух простых суждений: Сверкнула молния и Загремел гром. Конъюнкция может состоять не только из двух, но и из большего числа простых суждений. Например: Сверкнула молния, и загремел гром, и пошел дождь (а ? b ? с).
Дизъюнктивное суждение (дизъюнкция) – это сложное суждение с разделительным союзом ИЛИ. Вспомним, что, говоря о логических операциях сложения и умножения понятий, мы отмечали неоднозначность этого союза – он может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида: нестрогая и строгая дизъюнкция соответственно.
Нестрогая дизъюнкция – это сложное суждение с разделительным союзом ИЛИ в его нестрогом (неисключающем) значении, который обозначается знаком «?». С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a ? b (читается «а или b»), где а и b – это два простых суждения. Например, сложное суждение Он изучает английский, или он изучает немецкий является нестрогой дизъюнкцией (разделением) двух простых суждений: Он изучает английский и Он изучает немецкий. Эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, поэтому данная дизъюнкция является нестрогой.
Строгая дизъюнкция – это сложное суждение с разделительным союзом ИЛИ в его строгом (исключающем) значении, который обозначается знаком «?_». С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: а ?_ b (читается «или а, или b»), где а и b – это два простых суждения. Например, сложное суждение: Он учится в 9 классе, или он учится в 11 классе является строгой дизъюнкцией (разделением) двух простых суждений: Он учится в 9 классе, Он учится в 11 классе. Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.
Как нестрогая, так и строгая дизъюнкции могут состоять не только из двух, но и из большего числа простых суждений. Например: Он изучает английский, или он изучает немецкий, или он изучает французский (a ? b ? с); Он учится в 9 классе, или он учится в 10 классе, или он учится в 11 классе (a ?_ b ?_ c).
Импликативное суждение (импликация) – это сложное суждение с условным союзом ЕСЛИ…ТО, который обозначается знаком «=>». С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы: а => в (читается «если а, то b»), где а и b – это два простых суждения. Например, сложное суждение Если вещество является металлом, то оно электропроводно представляет собой импликативное суждение (причинно-следственную связь) двух простых суждений: Вещество является металлом и Вещество электропроводно. В данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом).
Первая часть импликации называется основанием, а вторая – следствием; из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации: а => b, можно прочитать так: «если а, то обязательно b, но если b, то не обязательно а».
Эквивалентное суждение (эквиваленция) – это сложное суждение с союзом ЕСЛИ…ТО не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентном). В данном случае этот союз обозначается знаком « », с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы: а b (читается «если а, то b, и если b, то а»), где а и b – это два простых суждения. Например, сложное суждение Если число является четным, то оно делится без остатка на 2 представляет собой эквивалентное суждение (равенство, тождество) двух простых суждений: Число является четным и Число делится без остатка на 2. Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число четное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно четное.
Понятно, что в эквиваленции (в отличие от импликации) не может быть ни основания, ни следствия, так как две ее части являются равнозначными суждениями.
Отрицательное суждение (отрицание) – это сложное суждение с союзом НЕВЕРНО, ЧТО, который обозначается знаком «¬». С помощью этого знака отрицательное суждение можно представить в виде формулы: ¬ а (читается «неверно, что а»), где а – это простое суждение. Здесь может возникнуть вопрос: где же вторая часть сложного суждения, которую мы обычно обозначали символом b? В записи ¬ а, уже присутствуют два простых суждения: а – это какое-то утверждение, а знак «¬» – его отрицание. Перед нами как бы два простых суждения – одно утвердительное, другое отрицательное. Пример отрицательного суждения: Неверно, что все мухи являются птицами.
Союзов в естественном языке много, но все они по смыслу сводятся к рассмотренным пяти видам, и любое сложное суждение относится к одному из них. Например, сложное суждение Уж полночь близится, а Германна все нет является конъюнкцией, потому что в нем союз А употребляется в роли соединительного союза И. Сложное суждение Посеешь ветер, пожнешь бурю, в котором вообще нет союза, является импликацией, так как два простых суждения в нем связаны условным союзом ЕСЛИ…ТО.
Приведем еще несколько примеров сложных суждений с различными союзами естественного языка, которые выступают в роли нескольких рассмотренных нами логических союзов.
Живое существо является человеком только тогда, когда оно обладает мышлением (эквиваленция).
• Человечество может погибнуть то ли от истощения земных ресурсов, то ли от экологической катастрофы, то ли в результате третьей мировой войны (нестрогая дизъюнкция).
• Вчера он получил двойку не только по математике, но еще и по русскому (конъюнкция).
• Проводник нагревается, когда через него проходит электрический ток (импликация).
• Окружающий нас мир либо познаваем, либо нет (строгая дизъюнкция).
• Либо же он совершенно бездарен, либо же полный лентяй (нестрогая дизъюнкция).
• Когда человек льстит, он лжет (импликация).
• Вода превращается в лед лишь при температуре от нуля градусов по Цельсию и ниже (эквиваленция).
Две прямые, лежащие в одной плоскости, не имеют общих точек только тогда, когда они параллельны (эквиваленция).
Вместо того, чтобы пойти в школу, он пошел гулять (конъюнкция).
Английский язык можно изучать либо в школе, либо на курсах, либо с репетитором, либо самостоятельно (нестрогая дизъюнкция).
То ли в мире действует всеобщая закономерность, то ли всеобщая случайность (строгая дизъюнкция).
Он не готовился к занятиям или систематически прогуливал их (нестрогая дизъюнкция).
Чем дальше в лес, тем больше дров (импликация).
Деревья качаются, потому что дует ветер (импликация).
Хотя на море разыгрался шторм, корабль неуклонно двигался своим курсом (конъюнкция).
• Глаза боятся, а руки делают (конъюнкция).
• Бели с утра шел дождь, то к полудню прояснилось (конъюнкция).
• Кончил дело, гуляй смело (импликация).
• Треугольник является равносторонним только тогда, когда все его углы равны (эквиваленция).
Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений. Ниже приведена таблица истинности всех видов сложных суждений в зависимости от всех возможных наборов истинностных значений двух входящих в них простых суждений. Таких наборов всего четыре:
• оба простых суждения истинные;
• первое суждение истинное, а второе ложное;
• первое суждение ложное, а второе истинное;
• оба суждения ложные.
Как видим, конъюнкция (а ? b) истинна только тогда, когда истинны оба простых суждения, входящих в нее. Надо отметить, что конъюнкция, состоящая не из двух, а из большего количества простых суждений, также истинна только в том случае, когда истинны все входящие в нее суждения. Во всех остальных случаях она является ложной.
Нестрогая дизъюнкция (a ? b), наоборот, истинна во всех случаях за исключением того, когда оба входящих в нее простых суждения ложны. Нестрогая дизъюнкция, состоящая не из двух, а из большего количества простых суждений, также ложна только тогда, когда ложны все входящие в нее простые суждения. Строгая дизъюнкция (а ?_ b) истинна только тогда, когда одно входящее в нее простое суждение истинно, а другое ложно. Строгая дизъюнкция, состоящая не из двух, а из большего количества простых суждений, истинна только в том случае, если истинно только одно из входящих в нее простых суждений, а все остальные ложны.
Импликация (а => b) ложна только в одном случае, – когда ее основание является истинным, а следствие ложным. Во всех остальных случаях она истинна.
Эквиваленция (а b) истинна тогда, когда два составляющих ее простых суждения истинны или же когда они оба являются ложными. Если одна часть эквиваленции истинна, а другая ложна, то эквиваленция ложна.
Проще всего определяется истинность отрицания: когда утверждение (а) истинно, его отрицание (¬ а) ложно; когда утверждение (а) ложно, его отрицание (¬ а) истинно.
Есть ли жизнь на Марсе? (Виды и правила вопросов)
Вопрос весьма близок к суждению. Это проявляется в том, что любое суждение можно рассматривать как ответ на некий вопрос. Поэтому вопрос – это логическая форма (конструкция), которая направлена на получение ответа в виде некоторого суждения.
Вопросы делятся на исследовательские и информационные.
Исследовательские вопросы направлены на получение нового знания. Это вопросы, на которые пока нет ответов, например: Как родилась Вселенная?
Информационные вопросы имеют своей целью приобретение (передачу от одного лица другому) уже имеющихся знаний (информации), например: Какова температура плавления свинца?
Вопросы также делятся на категориальные и пропозициональные.
Категориальные (восполняющие, специальные) вопросы включают в себя вопросительные слова кто, что, где, когда, почему, как и т. п., указывающие направление поиска ответов и, соответственно, категорию объектов, свойств или явлений, в которой следует искать нужные ответы. Категориальным, например, является вопрос Кто создал Периодическую систему химических элементов?
Пропозициональные (уточняющие, общие) вопросы направлены на подтверждение или отрицание некоей уже имеющейся информации. В этих вопросах ответ как бы уже заложен в виде готового суждения, которое надо лишь подтвердить или отвергнуть. Вопрос Полезно ли изучение математики? является пропозициональным.
Понятно, что и исследовательские, и информационные вопросы могут быть как категориальными, так и пропозициональными. Например: Как создать универсальное доказательство теоремы Ферма? – исследовательский категориальный вопрос; Есть ли во Вселенной планеты, населенные, как и Земля, разумными существами? – исследовательский пропозициональный вопрос; Когда появилась логика? – информационный категориальный вопрос; Верно ли, что число ? – это отношение длины окружности к ее диаметру? – информационный пропозициональный вопрос.
Приведем еще несколько примеров вопросов.
• Когда был открыт закон Всемирного тяготения? (информационный категориальный вопрос).
• Смогут ли жители Земли расселиться на других планетах Солнечной системы? (исследовательский пропозициональный вопрос).
• В каком году родился Наполеон? (информационный категориальный вопрос).
• Каково будущее человечества? (исследовательский категориальный вопрос).
• Возможно ли предотвратить третью мировую войну? (исследовательский пропозициональный вопрос).
• Что такое тригонометрия? (информационный категориальный вопрос).
• Можно ли измерить расстояние от Земли до Луны? (информационный пропозициональный вопрос).
• Кто является создателем квантовой теории? (информационный категориальный вопрос).
• Чем отличаются естественные науки от гуманитарных? (информационный категориальный вопрос).
• Вел ли Древний Рим продолжительные завоевательные войны? (информационный пропозициональный вопрос).
• В чем смысл человеческой жизни? (исследовательский категориальный вопрос).
• Где находится самое высокое место земного шара? (информационный категориальный вопрос).
• Чему равна скорость света? (информационный категориальный вопрос).
• Что такое любовь? (исследовательский категориальный вопрос).
• Верно ли, что геоцентрическая картина мира появилась еще в древности? (информационный пропозициональный вопрос).
• Как зародилась жизнь во Вселенной? (исследовательский категориальный вопрос).
Достигнут ли люди когда-нибудь всеобщего процветания? (исследовательский пропозициональный вопрос).
• Как доказывается теорема Пифагора? (информационный категориальный вопрос).
• Возможно ли полное преодоление социальной несправедливости? (исследовательский пропозициональный вопрос).
• Кто считается создателем формальной логики? (информационный категориальный вопрос).
Любой вопрос имеет определенную структуру и состоит из двух частей. Первая часть представляет собой некую информацию (выраженную, как правило, каким-нибудь суждением), а вторая часть указывает на ее недостаточность и необходимость ее дополнения каким-либо ответом. Первая часть, называется основной (базисной) (ее также иногда называют предпосылкой вопроса), а вторая часть – искомой. Например, в информационном категориальном вопросе Когда была создана теория электромагнитного поля? основная часть – это утвердительное суждение Была создана теория электромагнитного поля, а искомая часть, представленная вопросительным словом когда, указывает на недостаточность информации, содержащейся в базисной части вопроса, и требует ее дополнения, которое следует искать в области (категории) временных явлений.
В исследовательском пропозициональном вопросе Возможны ли полеты землян в другие галактики? основная часть представлена суждением Возможны полеты землян в другие галактики, а искомая часть, выраженная частицей ли, указывает на необходимость подтверждения или отрицания этого суждения. В данном случае искомая часть вопроса свидетельствует не об отсутствии какой-то информации, содержащейся в его базисной части, а об отсутствии знания о ее истинности или ложности и требует это знание получить.
Наиболее важное логическое требование к постановке вопроса заключается в том, чтобы его базисная часть была истинным суждением. В этом случае вопрос считается логически корректным. Если же основная часть вопроса представляет собой ложное суждение, то вопрос следует признать логически некорректным (подобные вопросы не требуют ответа и подлежат отвержению).
Например, вопрос Когда было предпринято первое кругосветное путешествие? является логически корректным, поскольку его основная часть выражена истинным суждением В истории человечества имело место первое кругосветное путешествие. Вопрос В каком году знаменитый английский ученый Исаак Ньютон закончил работу над общей теорией относительности? логически некорректен, так как его основная часть представлена ложным суждением Автором общей теории относительности является знаменитый английский ученый Исаак Ньютон.
Итак, основная (базисная) часть вопроса должна быть истинной и не должна быть ложной. Однако существуют логически корректные вопросы, основные части которых являются ложными суждениями. Например, вопросы Возможно ли создание вечного двигателя? Есть ли разумная жизнь на Марсе? Изобретут ли машину времени? несомненно, следует признать логически корректными, несмотря на то, что их базисные части представляют собой ложные суждения: Возможно создание вечного двигателя, Есть разумная жизнь на Марсе, Изобретут машину времени. Дело в том, что искомые части этих вопросов направлены на выяснение истинностных значений их базисных частей, т. е. требуется выяснить, истинными или ложными являются суждения Возможно создание вечного двигателя, Есть разумная жизнь на Марсе, Изобретут машину времени. В этом случае вопросы логически корректны. Если бы искомые части рассматриваемых вопросов не были направлены на выяснение истинности их основных частей, а имели бы своей целью нечто иное, эти вопросы являлись бы логически некорректными, например: Где был создан первый вечный двигатель? Когда появилась разумная жизнь на Марсе? Сколько будет стоить путешествие на машине времени?
Таким образом, главное правило постановки вопроса следует расширить и уточнить: основная (базисная) часть корректного вопроса должна быть истинным суждением. Если же она является ложным суждением, то его искомая часть должна быть направлена на выяснение истинностного значения основной части; в противном случае вопрос будет логически некорректным.
Нетрудно догадаться, что требование для основной части быть истинной, по преимуществу, относится к категориальным вопросам, а требование того, чтобы искомая часть была выяснением истинности основной части, относится к пропозициональным вопросам.
Надо отметить, что корректные категориальные и пропозициональные вопросы сходны между собой в том, что на них всегда можно дать истинный ответ (как, впрочем, и ложный). Например, на категориальный вопрос Когда закончилась Первая мировая война? можно дать как истинный ответ (В 1918 году), так и ложный (В 1916 году). На пропозициональный вопрос Вращается ли Земля вокруг Солнца? также можно дать как истинный ответ (Да, вращается), так и ложный (Нет, не вращается). Отметим, что оба приведенных вопроса логически корректны.
Итак, принципиальная возможность получения истинных ответов есть основной признак корректных вопросов. Если же получить истинные ответы на некие вопросы принципиально невозможно, то они являются некорректными.
Например, нельзя получить истинный ответ на пропозициональный вопрос Закончится ли когда-нибудь Первая мировая война? так же, как невозможно получить его на категориальный вопрос С какой скоростью вращается Солнце вокруг неподвижной Земли? Любые ответы на эти вопросы необходимо будет признать неудовлетворительными, а сами вопросы – логически некорректными, подлежащими отвержению.
- Тест по логике. вариант 1
- Параллельные прямые — определение и вычисление с примерами решения
- Определения параллельных прямых
- Признаки параллельности двух прямых
- Аксиома параллельных прямых
- Обратные теоремы
- Пример №1
- Параллельность прямых на плоскости
- Две прямые, перпендикулярные третьей
- Накрест лежащие, соответственные и односторонние углы
- Признаки параллельности прямых
- Пример №2
- Пример №3
- Пример №4
- Аксиома параллельных прямых
- Пример №5
- Пример №6
- Свойства параллельных прямых
- Пример №7
- Пример №8
- Углы с соответственно параллельными и соответственно перпендикулярными сторонами
- Расстояние между параллельными прямыми
- Пример №9
- Пример №10
- Справочный материал по параллельным прямым
- Перпендикулярные и параллельные прямые
- 💡 Видео
Видео:Практикум суждениеСкачать

Тест по логике. вариант 1
| [ Скачать с сервера (2.00Mb) ] | 31.10.2013, 19:28 | |||
| вариант 1. 1. что относится к формам мышления? а) доказательство, опровержение б) прямая и косвенная аргументация в) понятие, суждение, умозаключение г) ощущение, восприятие, представление Ответ: в) понятие, суждение, умозаключение 2. операция, раскрывающая объем понятия, это – Ответ: а) определение 3. понятие «спортсмен» и «футболист» находятся в отношении Ответ: б) подчинения 4. Создатель логики: Ответ: в) Аристотель 5. В структуру доказательства входят: а) посылки и термины б) тезис, антитезис, аргументы и контраргументы в) тезис, аргументы, демонстрация г) ничто из вышеперечисленного Ответ: в) тезис, аргументы, демонстрация 6. Ошибка «предвосхищение основания» возникает в доказательстве тогда, когда а) в качестве аргумента используется суждение, которое само нуждается в доказательстве б) в качестве аргумента используется ложное суждение в) аргумент доказывается на основе тезиса г) аргумент неясно сформулирован Ответ: а) в качестве аргумента используется суждение, которое само нуждается в доказательстве 7. «Две прямые на плоскости параллельны и пересекаются» а) нарушен закон достаточного основания б) нарушены закон противоречия и закон исключенного третьего в) нарушены все законы г) нарушен закон тождества размышления: две прямые на плоскости могут быть параллельны, пересекаться, могут быть скрещивающимися прямыми. Ответ: г) нарушен закон тождества 8. Закон исключенного третьего формулируется так: а) из двух противоречащих суждений одно истинно, другое – ложно. б) два противоположных или противоречащих суждения не могут быть вместе истинными в) Каждая мысль на протяжении всего процесса рассуждения должна быть тождественна сама себе г) А истинно, если для этого есть достаточное основание В. Ответ: а) из двух противоречащих суждений одно истинно, другое – ложно. 9. Какой вывод из следующих посылок «Все металлы – теплопроводные вещества», «Все металлы – электропроводные вещества» а) Все электропроводные вещества – металлы б) некоторые электропроводные вещества – теплопроводные в) все электропроводные вещества являются теплопроводными г) все теплопроводные вещества являются электропроводными Ответ: б) некоторые электропроводные вещества – теплопроводные 10. Ошибка «круг в доказательстве» возникает тогда, когда а) в доказательстве исходят из ложных аргументов б) в качестве аргумента используют суждение, истинность которого нуждается в обосновании в) в качестве аргумента используется суждение, противоречащее другим аргументам г) в качестве аргумента используется суждение, истинность которого доказана с помощью тезиса Ответ: г) в качестве аргумента используется суждение, истинность которого доказана с помощью тезиса 11. (3 балла) Какие из следующих умозаключений являются правильными? 1.Все солдаты носят ремни. Некоторые солдаты храбрые. Некоторые храбрецы не носят ремни. 2. Если произведение художественно, то оно правдиво. Это произведение является художественным, т.к. оно является правдивым. 3. Все выдающиеся люди в истории были чрезвычайно трудолюбивы. Мой дед был чрезвычайно трудолюбивым человеком, поэтому его также следует считать выдающимся в истории человеком. а) ни одно не правильно б) все правильны 1 . имеем дело с 3 фигурой категорического силлогизма. модус AIO не правильный. 2. условно – категорическое умозаключение с модусом: от утверждения истинности следствия к утверждению истинности основания – достоверных выводов не дает. 3. средний термин не распределен ни в одной из посылок. вывод не достоверный. Ответ: а) ни одно не правильно 12. Какой закон логики нарушен в следующем рассуждении: « Однажды падишах спросил Барбала: «Скажи мне, сколько останется, если из двенадцати отнять четыре». – «Ничего не останется» — ответил Бирбал. .. 19. Логический квадрат: если Частноутвердительное суждение (I) истинно, то общеотрицательное сравнимое суждение (Е) будет: а) только ложным б) либо истинным, либо ложным в) только истинным 20. суждению «Ничто человеческое мне не чуждо» будет противоречить суждение: а) все человеческое мне чуждо б) нечто человеческое мне чуждо в) не все человеческое мне не чуждо г) ничто не противоречит размышления: имеем дело с общеотрицательным суждением (Е). ему противоречащим является Частноутвердительное (I) Ответ: б) нечто человеческое мне чуждо 21. К совместимым суждениям относят 2)противоположные (контрарные суждения) размышления: К совместимым относятся суждения, которые одновременно могут быть истинными. Различают три вида совместимости: 1) эквивалентность(полная совместимость), 2) частичная совместимость (субконтрарность) и 3)подчинение. 22. Частноутвердительное суждение имеет форму: б) неверно, что все S не суть Р в) некоторое S суть Р г) Это S не есть Р Ответ: в) некоторое S суть Р 23. Какое суждение находится в отношении подчинения к суждению : « Все юмористы – веселые люди» а) некоторые юмористы – веселые люди б) некоторые юмористы – не веселые люди в) все юмористы не являются веселыми людьми г) не все юмористы не являются веселыми людьми размышления: исходное суждение общеутвердительное суждение (А). в отношении подчинения у него находится Частноутвердительное суждение (I). Ответ: а) некоторые юмористы – веселые люди. 24. Какая схема соответствует отношению объемов понятий « книга» (А), «печатное издание» (В), « сувенир» (С). размышления: некоторые сувениры (С) это книги (А). объемы понятий должны пересекаться. любая книга (А) это печатное издание (В). объем А должен входить в объем В. Некоторые сувениры (С) являются печатными изданиями(В). также пересечение объемов. 25. правильно ли следующее умозаключение: Все планеты – небесные тела. Луна не является планетой, следовательно она не является небесным телом? размышления: имеем дело с 1 фигурой категорического силлогизма. термин «небесное тело» был распределен в большей посылке, а в заключении не распределен. значит вывод не верный. 26. какое правило доказательства нарушено в следующем рассуждении « Мы должны проголосовать за этого кандидата, т.к. он – человек интеллигентный, и имеет хорошую предвыборную программы»? а) ложный аргумент б) предвосхищение основания в) тезис не следует из аргументов г) подмена тезиса Ответ: в) тезис не следует из аргументов 27. (3 балла) Инспектору Борисову стало известно, что совершена кража в ювелирном магазине. Он знал, что это мог сделать либо недавно вышедший на свободу матерый уголовник по кличке Лось, либо появившийся в городе А. Рубашкин по кличке Артист, либо начинающий вор Павел Смышляев. Вскоре инспектору поступила информация: 1)ювелирный магазин ограбил не Артист 2)магазин обворовал Смышляев. Спустя некоторое время выяснилось, что только одно из этих сообщений соответствует действительности. Этого оказалось достаточно, чтобы инспектор установил вора. кто это сделал? размышления: если правильное 2ое утверждение: смышляев ограбил, то вместе с ним будет правильным, что не артист ограбил(а по условию, только одно может быть истинным суждением) значит истинно 1 ое утверждение: не артист ограбил, при этом что это сделал Смышляев будет ложью, и вывод это сделал Лось. 32,014 просмотров всего, 5 просмотров сегодня Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать  Параллельные прямые — определение и вычисление с примерами решенияСодержание: Параллельные прямые: Ранее мы уже дали определение параллельных прямых. Напомним, что две прямые на плоскости называются параллельными, если они не пересекаются. Например, если две прямые a и b плоскости перпендикулярны прямой c этой плоскости, то они не пересекаются, т. е. параллельны (рис. 85, а). Этот факт нами был доказан как следствие из теоремы о существовании и единственности перпендикуляра, проведенного из точки к данной прямой. Два отрезка называются параллельными, если они лежат на параллельных прямых. Отрезок называется параллельным прямой, если он лежит на прямой, параллельной данной прямой. Например, на рисунке 85, B изображены параллельные отрезки АВ и СD (параллельность отрезков АВ и СD обозначается следующим образом: АВ Аналогично определяется параллельность двух лучей, отрезка и прямой, луча и прямой, а также отрезка и луча. Например, на рисунке 85, в изображены отрезок PQ, параллельный прямой l, и отрезок ТК, параллельный лучу СD. Видео:Параллельность прямой к плоскостиСкачать  Определения параллельных прямыхНа рисунке 10 прямые Это можно записать так: На плоскости две прямые могут либо пересекаться, либо не пересекаться. Прямые на плоскости, которые не пересекаются, называются параллельными. Если прямые Две прямые, которые при пересечении образуют прямой угол, называются перпендикулярными прямыми. Если прямые ВАЖНО! Совпадающие прямые будем считать одной прямой. Поэтому, если сказано «даны две прямые», это означает, что даны две различные несовпадающие прямые. Это касается также точек, лучей, отрезков и других фигур. Есть два способа практического сравнения длин отрезков, а также величин углов: 1) наложение; 2) сравнение результатов измерения. Оба способа являются приближенными. В геометрии отрезки и углы могут быть равны, если это дано по условию либо следует из условия на основании логических рассуждений. Признаки параллельности двух прямыхПрямая c называется секущей по отношению к прямым a и b, если она пересекает каждую из них в различных точках. При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 86, а обозначены цифрами. Некоторые пары этих углов имеют специальное название:
Рассмотрим признаки параллельности двух прямых. Теорема 1 (признак параллельности прямых по равенству внутренних накрест лежащих углов). Если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны.
Например, пусть прямая l проходит через точку F, принадлежащую стороне АС треугольника АВС, так, что Теорема 2 (признак параллельности прямых по равенству соответственных углов). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. 1) Пусть при пересечении прямых а и b секущей с соответственные углы равны, например
3) Из равенств Например, пусть прямая l пересекает стороны AB и АС треугольника ABC в точках О и F соответственно и Теорема 3 (признак параллельности прямых по сумме градусных мер внутренних односторонних углов). Если, при пересечении двух прямых секущей сумма градусных мер внутренних односторонних углов равна 180°, то прямые параллельны.
Аксиома параллельных прямыхКак уже отмечалось, при доказательстве теорем опираются на уже доказанные теоремы и некоторые исходные утверждения, которые называются аксиомами. Познакомимся еще с одной аксиомой, имеющей важное значение для дальнейшего построения геометрии. Пусть в плоскости дана прямая а и не лежащая на ней произвольная точка О. Можно доказать, что через точку О в этой плоскости проходит прямая, параллельная прямой а. Действительно, проведем через точку О прямую с, перпендикулярную прямой a, затем прямую b, перпендикулярную прямой с. Так как прямые а и b перпендикулярны прямой с, то они не пересекаются, т. е. параллельны (рис. 92). Следовательно, через точку O Большой вклад в решение этого вопроса внес русский математик Н. И. Лобачевский (1792—1856). Таким образом, в качестве одной из аксиом принимается аксиома параллельных прямых, которая формулируется следующим образом. Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Непосредственно из аксиомы параллельны х прямых в качестве следствий получаем следующие теоремы. Теорема 1. Если две прямые параллельны третьей прямой, то они параллельны. Пусть прямые а и b параллельны прямой с. Докажем, что а Например, пусть прямые а и b пересекают сторону FС треугольника FDС так, что Теорема 2. Пусть три прямые лежат в плоскости. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую. Пусть прямые а и b параллельны, а прямая с пересекает прямую а в точке О (рис. 94, а). Докажем, что прямая с пересекает прямую b. Проведем доказательство методом от противного. Допустим, что прямая с не пересекает прямую b. Тогда через точку О проходят две прямые а и с, не пересекающие прямую b, т. е. параллельные ей (рис. 94, б). Но это противоречит аксиоме параллельных прямых. Следовательно, наше предположение неверно и прямая с пересекает прямую b. Обратные теоремыВ формулировке любой теоремы можно выделить две ее части: условие и заключение. Условие теоремы — это то, что дано, а заключение — то, что требуется доказать. Например, рассмотрим признак параллельности прямых: если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны. В этой теореме условием является первая часть утверждения: при пересечении двух прямых секущей внутренние накрест лежащие углы равны (это дано), а заключением — вторая часть: прямые параллельны (это требуется доказать). Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением — условие данной теоремы. Теперь докажем теоремы, обратные признакам параллельности прямых. Теорема 3 (о равенстве внутренних накрест лежащих углов). Если две параллельные прямые пересечены секущей, то внутренние накрест лежащие углы равны. 1) Пусть параллельные прямые а и b пересечены секущей AВ (рис. 95, а). Докажем, что внутренние накрест лежащие углы, например 1 и 2, равны. 2) Доказательство теоремы проведем методом от противного. Допустим, что углы 1 и 2 не равны. Отложим угол QАВ, равный углу 2, так, чтобы угол QАВ и 3) По построению накрест лежащие углы QАВ и Например, пусть прямая l параллельна стороне ВС треугольника АВС (рис. 95, б). Тогда Теорема 4 (о равенстве соответственных углов). Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Например, пусть прямая l параллельна биссектрисе AF треугольника ABC (рис. 96, б), тогда Теорема 5 (о свойстве внутренних односторонних углов). Если две параллельные прямые пересечены секущей, то сумма градусных мер внутренних односторонних углов равна 180°. 1) Пусть параллельные прямые а и b пересечены секущей с. Докажем, например, что 2) Так как прямые а и b параллельны, то по теореме 4 справедливо равенство 3) Углы 2 и 3 смежные, следовательно, 4) Из равенств Например, пусть отрезок FT параллелен стороне АВ треугольника ABC (рис. 97, б). Тогда Заметим, если доказана какая-либо теорема, то отсюда еще не следует, что обратная теорема верна. Например, известно, что вертикальные углы равны, но если углы равны, то отсюда не вытекает, что они являются вертикальными. Пример №1Докажите, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой прямой. 1) Пусть прямые а и b параллельны и с 2) Так как прямая с пересекает прямую а, то она пересекает и прямую b. 3) При пересечении параллельных прямых а и b секущей с образуются равные внутренние накрест лежащие углы 1 и 2. Так как Что и требовалось доказать. Видео:Логика Лекция 8 ГипотезаСкачать  Параллельность прямых на плоскостиПараллельность прямых — одно из основных понятий геометрии. Параллельность часто встречается в жизни. Посмотрев вокруг, можно убедиться, что мы живем в мире параллельных линий. Это края парты, столбы вдоль дороги, полоски «зебры» на пешеходном переходе. Две прямые, перпендикулярные третьейОпределение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Лучи и отрезки называются параллельными, если они лежат на параллельных прямых. Если прямые Вы уже знаете теорему о параллельных прямых на плоскости: «Две прямые, перпендикулярные третьей, параллельны между собой». Другими словами, если Данная теорема позволяет решить две важные практические задачи. Первая задача заключается в проведении нескольких параллельных прямых. Пусть дана прямая Вторая задача — проведение прямой, параллельной данной и проходящей через точку, не лежащую на данной прямой. По рисунку 163 объясните процесс проведения прямой Из построения следует: так как Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной. Накрест лежащие, соответственные и односторонние углыПри пересечении двух прямых Некоторые пары этих углов имеют специальные названия:
На рисунке 165 отмечены углы 1 и 2. Они являются внутренними накрест лежащими углами при прямых ВС и AD и секущей BD. В этом легко убедиться, продлив отрезки ВС, AD и BD. Признаки параллельности прямыхС указанными парами углов связаны следующие признаки параллельности прямых. Теорема (первый признак параллельности прямых). Если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны. Дано: Доказать: Доказательство: Из середины М отрезка АВ опустим перпендикуляр МК на прямую Теорема (второй признак параллельности прямых). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Дано: Доказать: Доказательство: Углы 1 и 3 равны как вертикальные. А так как углы 1 и 2 равны по условию, то углы 2 и 3 равны между собой. Но углы 2 и 3 — внутренние накрест лежащие при прямых Теорема (третий признак параллельности прямых). Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180°, то прямые параллельны. Дано: Доказать: Доказательство: Углы 1 и 3 — смежные, поэтому их сумма равна 180°. А так как сумма углов 1 и 2 равна 180° по условию, то углы 2 и 3 равны между собой. Но углы 2 и 3 — внутренние накрест лежащие при прямых Пример №2Доказать, что если отрезки AD и ВС пересекаются и точкой пересечения делятся пополам, то прямые АВ и CD параллельны. Доказательство: Пусть О — точка пересечения отрезков AD и ВС (рис. 169). Треугольники АОВ и DOC равны по двум сторонам и углу между ними ( Пример №3На биссектрисе угла ВАС взята точка К, а на стороне АС — точка D, Доказательство: Так как АК — биссектриса угла ВАС (рис. 170), то
Углы ADK и ВАС — внутренние односторонние при прямых KD и ВА и секущей АС. А поскольку Пример №4Биссектриса ВС угла ABD отсекает на прямой а отрезок АС, равный отрезку АВ. Доказать, что прямые а и b параллельны (рис. 171). Доказательство: Так как ВС — биссектриса угла ABD, то Реальная геометрия На рисунке 184 изображен электронный угломер — инструмент для нанесения параллельных линий на рейке или доске. Прибор состоит из двух частей, скрепленных винтом. Одна часть неподвижная, она прижимается к доске, а другая поворачивается на необходимый угол, градусная мера которого отражается на экране угломера. Зажав винт, закрепляют нужный угол. Сдвинув неподвижную часть угломера вдоль доски, наносят новую линию разметки. Так получают параллельные линии, по которым затем распиливают доску. Аксиома параллельных прямыхВы уже знаете, что на плоскости через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной (см. § 15). Из пятого постулата Евклида (постулат — аксиоматическое предположение) следует, что такая прямая — единственная. На протяжении двух тысячелетий вокруг утверждения о единственности параллельной прямой разыгрывалась захватывающая и драматичная история! Со времен Древней Греции математики спорили о том, можно доказать пятый постулат Евклида или нет. То есть это теорема или аксиома? В конце концов работы русского математика Н. И. Лобачевского (1792—1856) позволили выяснить, что доказать пятый постулат нельзя. Поэтому это утверждение является аксиомой. Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Если прямая Поиски доказательства пятого постулата Евклида привели к развитию математики и физики, к пересмотру научных представлений о геометрии Вселенной. Решая проблему пятого постулата, Лобачевский создал новую геометрию, с новыми аксиомами, теоремами, отличающуюся от геометрии Евклида, которая теперь так и называется — геометрия Лобачевского. Вы уже знаете, что на плоскости две прямые, перпендикулярные третьей, параллельны между собой. А если две прямые параллельны третьей прямой, то что можно сказать про первые две прямые? На этот вопрос отвечает следующая теорема. Теорема (о двух прямых, параллельных третьей). На плоскости две прямые, параллельные третьей, параллельны между собой. Дано: Доказать: Доказательство: Предположим, что прямые Метод доказательства «от противного» При доказательстве теоремы о двух прямых, параллельных третьей, мы применили метод доказательства от противного (то есть «от противоположного»). Суть его в следующем. Утверждение любой теоремы делится на условие — то, что в теореме дано, и заключение — то, что нужно доказать. В доказанной выше теореме условие: «Каждая из двух прямых параллельна третьей прямой», а заключение: «Эти две прямые параллельны между собой». Используя метод от противного, предполагают, что из данного условия теоремы следует утверждение, противоположное (противное) заключению теоремы. Если при сделанном предположении путем логических рассуждений приходят к какому-либо утверждению, противоречащему аксиомам или ранее доказанным теоремам, то сделанное предположение считается неверным, а верным — ему противоположное. В доказательстве нашей теоремы мы предположили, что эти две прямые не параллельны, а пересекаются в точке. И пришли к выводу, что тогда нарушается аксиома параллельных прямых. Следовательно, наше предположение о пересечении прямых не верно, а верно ему противоположное: прямые не пересекаются, то есть параллельны. Методом от противного ранее была доказана теорема о двух прямых, перпендикулярных третьей. Данный метод является очень мощным логическим инструментом доказательства. Причем не только в геометрии, но и в любом аргументированном споре. Теорема. Если на плоскости прямая пересекает одну из двух параллельных прямых, то она пересекает и другую прямую. Пример №5На рисунке 188 Доказательство: Так как накрест лежащие углы 1 и 2 равны, то Пример №6Доказать, что если сумма внутренних односторонних углов при двух данных прямых и секущей меньше 180°, то эти прямые пересекаются. Доказательство: Пусть Отложим от луча АВ угол 3, который в сумме с углом 1 дает 180°. Получим прямую Свойства параллельных прямыхВы знаете, что если две прямые пересечены секущей и накрест лежащие углы равны, то прямые параллельны. Это признак параллельности прямых. Обратное утверждение звучит так: «Если две прямые параллельны и пересечены секущей, то накрест лежащие углы равны». Это утверждение верно, и оно выражает свойство параллельных прямых. Докажем его и два других свойства для соответственных и односторонних углов. Теорема (о свойстве накрест лежащих углов при параллельных прямых и секущей). Если две параллельные прямые пересечены секущей, то внутренние накрест лежащие углы равны. Дано: Доказать: Доказательство: Предположим, что Теорема (о свойстве соответственных углов при параллельных прямых и секущей). Если две параллельные прямые пересечены секущей, то соответственные углы равны. Дано: Доказать: Доказательство: Углы 1 и 3 равны как накрест лежащие при параллельных прямых Теорема (о свойстве односторонних углов при параллельных прямых и секущей). Если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 180°. Дано: Доказать: Доказательство: Углы 2 и 3 — смежные. По свойству смежных углов Следствие. Прямая, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой прямой. На рисунке 198 Доказанные нами теоремы о свойствах углов при двух параллельных прямых и секущей являются обратными признакам параллельности прямых. Чтобы не путать признаки и свойства параллельных прямых, нужно помнить следующее:
Пример №7Доказать, что если отрезки АВ и CD равны и параллельны, а отрезки AD и ВС пересекаются в точке О, то треугольники АОВ и DOC равны. Доказательство: Углы BAD и CD А равны как накрест лежащие при параллельных прямых АВ и CD и секущей AD (рис. 199). Углы ABC и DCB равны как накрест лежащие при параллельных прямых АВ и CD и секущей ВС. Тогда Пример №8Доказать, что отрезки параллельных прямых, заключенные между двумя другими пересекающими их параллельными прямыми, равны между собой. Доказательство: Пусть АВ || CD, ВС || AD (рис. 200). Докажем, что АВ = CD, ВС=AD. Проведем отрезок BD. У треугольников ABD и CDB сторона BD — общая, Геометрия 3D Две плоскости называются параллельными, если они не имеют общих точек (не пересекаются). Если плоскости Существует еще один вид многогранников — призмы (рис. 212). У призмы две грани (основания) — равные многоугольники, которые лежат в параллельных плоскостях, а остальные грани (боковые) — параллелограммы (задача 137). У прямой призмы боковые грани — прямоугольники, боковые ребра перпендикулярны плоскостям оснований и равны между собой. На рисунке 212 изображены треугольная и четырехугольная прямые призмы. У них параллельны плоскости верхней и нижней граней. Углы с соответственно параллельными и соответственно перпендикулярными сторонамиТеорема (об углах с соответственно параллельными сторонами). Углы с соответственно параллельными сторонами или равны (если оба острые или оба тупые), или в сумме составляют 180° (если один острый, а другой тупой). 1) Острые углы 1 и 2 (рис. 213, а) — это углы с соответственно параллельными сторонами. Используя рисунок, докажите самостоятельно, что углы 1 и 2 равны. 2) Острый угол 1 и тупой угол 2 (рис. 213, б) — это углы с соответственно параллельными сторонами. Используя этот рисунок и результат пункта 1), докажите, что сумма углов 1 и 2 равна 180°. Теорема (об углах с соответственно перпендикулярными сторонами). Углы с соответственно перпендикулярными сторонами или равны (если оба острые или оба тупые), или в сумме составляют 180° (если один острый, а другой тупой). Доказательство: 1) Острые углы 1 и 2 — это углы с соответственно перпендикулярными сторонами (рис. 214, а). Построим острый угол 3 в вершине угла 1, стороны которого параллельны сторонам угла 2. Стороны угла 3 перпендикулярны сторонам угла 1 (прямая, перпендикулярная одной из параллельных прямых, перпендикулярна и другой прямой). По предыдущей теореме 2) Острый угол 1 и тупой угол 2 — это углы с соответственно перпендикулярными сторонами (рис. 214, б). Используя этот рисунок и результат пункта 1), докажите самостоятельно, что сумма углов 1 и 2 равна 180°. Запомнить:
Расстояние между параллельными прямымиОпределение. Расстоянием между параллельными прямыми называется расстояние от точки одной из этих прямых до другой прямой. Если Теорема (о расстоянии между параллельными прямыми). Все точки каждой из двух параллельных прямых равноудалены от другой прямой. Дано: Доказать: АВ = CD (рис. 285). Доказательство: Проведем отрезок AD. Углы CAD и BDA равны как внутренние накрест лежащие при параллельных прямых Следствие. Все точки, лежащие в одной полуплоскости относительно данной прямой и равноудаленные от этой прямой, лежат на прямой, параллельной данной. Доказательство: Пусть перпендикуляры АВ и CD к прямой В силу того что прямая, перпендикулярная к одной из двух параллельных прямых, будет перпендикулярна и к другой прямой, перпендикуляр АВ к прямой Пример №9В четырехугольнике ABCD АВ || CD, AD || ВС, АВ = 32 см, Решение:
Тогда Расстояние между параллельными прямыми измеряется длиной перпендикуляра, опущенного из любой точки одной из прямых на другую прямую. Опустим перпендикуляр ВН на прямую AD. В прямоугольном треугольнике АВН катет ВН лежит против угла в 30°. Поэтому он равен половине гипотенузы. Значит, ВН = Пример №10Найти геометрическое место точек, равноудаленных от двух данных параллельных прямых. Решение: 1) Пусть Тогда 2) Пусть некоторая точка М (см. рис. 287) равноудалена от прямых Таким образом, все точки прямой Геометрия 3D Расстоянием между параллельными плоскостями называется длина перпендикуляра, опущенного из точки, принадлежащей одной из плоскостей, на другую плоскость (рис. 290). В вашем классе пол и потолок — части параллельных плоскостей. Расстояние между ними равно высоте классной комнаты. Высотой прямой призмы называется расстояние между плоскостями оснований. Отрезок КК1 — перпендикуляр к плоскости ABC, равный ее высоте. У прямой призмы боковые ребра перпендикулярны плоскостям оснований. Поэтому высота призмы равна длине бокового ребра, то есть АА1 = КК1 (рис. 291). Запомнить:
Справочный материал по параллельным прямымПараллельные прямые
Признаки параллельности двух прямых
Свойства параллельных прямых
Перпендикулярные и параллельные прямыеДве прямые называют взаимно перпендикулярными, если они пересекаются под прямым углом. На рисунке 264 прямые На рисунке 265 прямые Основное свойство параллельных прямых (аксиома параллельности прямых). Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Углы, образованные при пересечении двух прямых секущей. Признаки и свойство параллельности прямых. Свойства углов, образованных при пересечении двух параллельных прямых секущей Прямую с называют секущей для прямых Пары углов 4 и 5; 3 и 6 называют внутренними односторонними; пары углов 4 и 6; 3 и 5 — внутренними накрест лежащими; пары углов 1 и 5; 2 и 6; 3 и 7; 4 и 8 — соответственными углами. Признаки параллельности прямых:
Свойство параллельных прямых. Две прямые, параллельные третьей прямой, параллельны друг другу.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. 💡 ВидеоЛиния пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать  Логика. 1. ПонятиеСкачать  Уравнение параллельной прямойСкачать  Логика. 6.1. Непосредственные умозаключения. Превращение. ОбращениеСкачать  Логика. Лекция 8. Силлогизмы. Категорические суждения. Продолжение.Скачать  Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать  Логика. 8.1. Категорический силлогизмСкачать  Сложение двух сил, направленных по одной прямой | Физика 7 класс #22 | ИнфоурокСкачать  Логика. 2.4. Логический квадратСкачать  Взаимное пересечение поверхностей (способ секущих плоскостей) Задача 48/Рабочая тетрадьСкачать  Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать  Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать  Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать  Лекция 5. Поверхности вращения. часть 1.Скачать  Усеченный конус: проекции сечения, изометрия и развертка поверхностиСкачать  Распределённые и параллельные вычисления 2. Виды соединений, параллелизмСкачать  | ||||

















 ). Отрезки ЕF и АВ не параллельны (это обозначается так: ЕF
). Отрезки ЕF и АВ не параллельны (это обозначается так: ЕF 
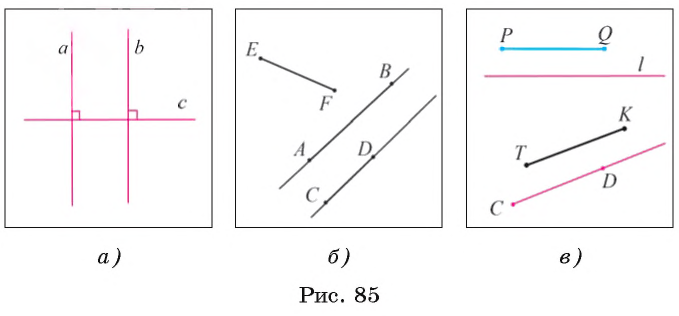
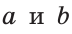 имеют общую точку М. Точка А принадлежит прямой
имеют общую точку М. Точка А принадлежит прямой 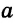 , но не принадлежит прямой
, но не принадлежит прямой 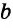 . Говорят, что прямые
. Говорят, что прямые 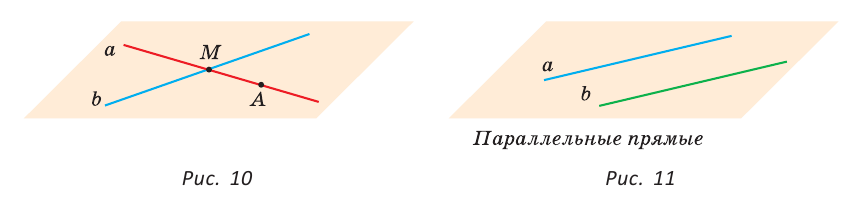
 — знак принадлежности точки прямой, «
— знак принадлежности точки прямой, « » — знак пересечения геометрических фигур.
» — знак пересечения геометрических фигур.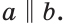
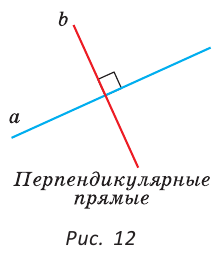
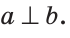
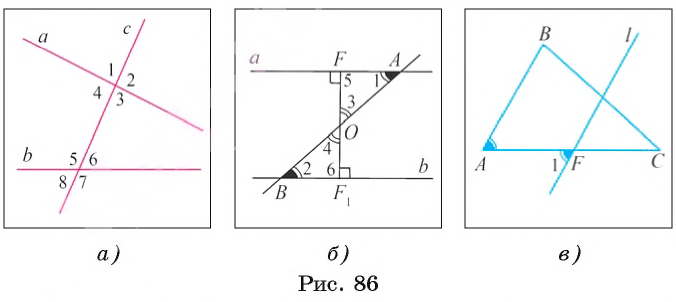
 1 =
1 = 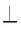 АВ и b
АВ и b  90°, то из середины О отрезка АВ проведем отрезок ОF
90°, то из середины О отрезка АВ проведем отрезок ОF  ОFА =
ОFА = 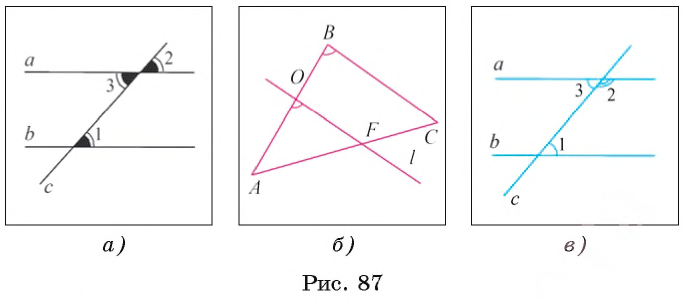
 a проходит прямая b, параллельная прямой а. Возникает вопрос: сколько можно провести через точку О прямых, параллельных прямой а? Ответ на него не является очевидным. Оказывается, что утверждение о единственности прямой, проходящей через данную точку и параллельной прямой, не может быть доказано на основании остальных аксиом Евклида и само является аксиомой.
a проходит прямая b, параллельная прямой а. Возникает вопрос: сколько можно провести через точку О прямых, параллельных прямой а? Ответ на него не является очевидным. Оказывается, что утверждение о единственности прямой, проходящей через данную точку и параллельной прямой, не может быть доказано на основании остальных аксиом Евклида и само является аксиомой.
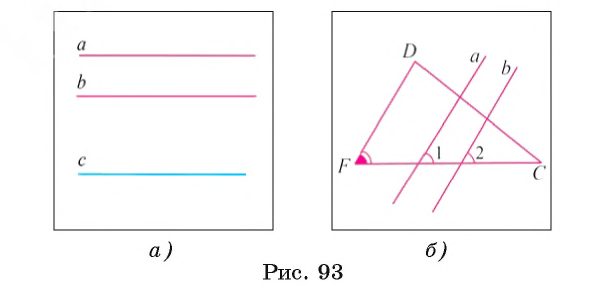
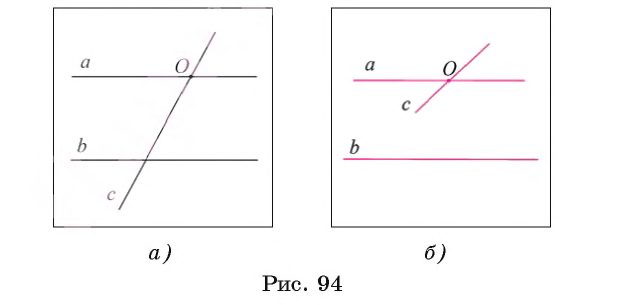
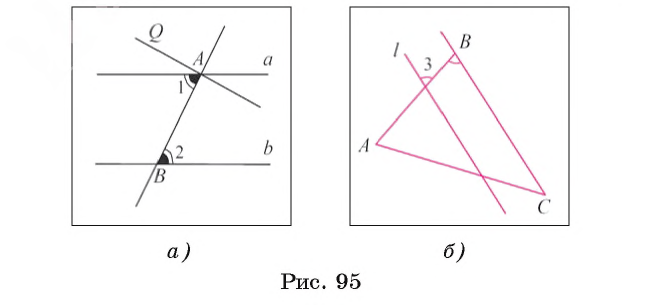
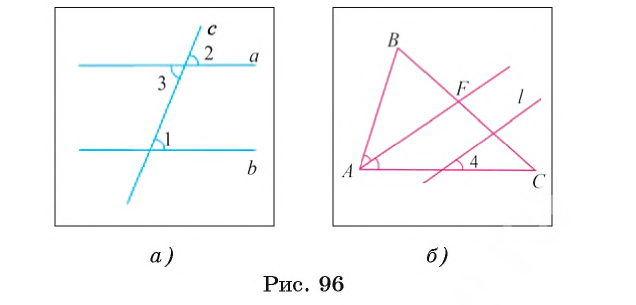
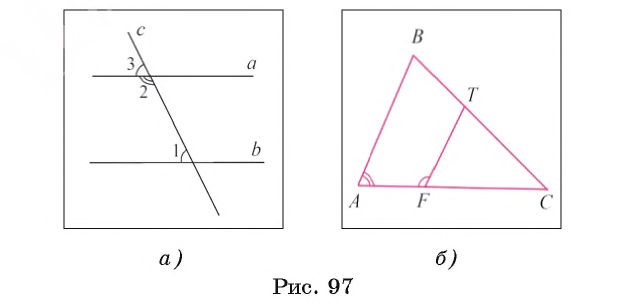
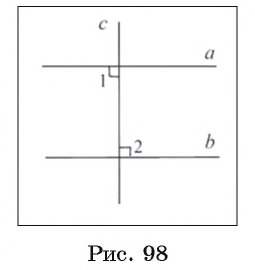
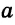 и
и 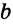 параллельны, то есть
параллельны, то есть 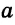
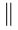
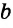 (рис. 160), то параллельны отрезки АВ и МК, отрезок МК и прямая
(рис. 160), то параллельны отрезки АВ и МК, отрезок МК и прямая 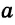 , лучи АВ и КМ.
, лучи АВ и КМ.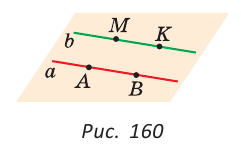
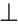
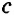 ,
, 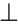
 , то
, то 
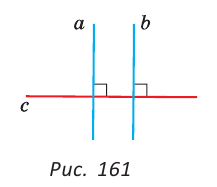
 , перпендикулярную прямой
, перпендикулярную прямой 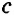 , затем — третью прямую
, затем — третью прямую 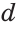 и т. д. Поскольку прямые
и т. д. Поскольку прямые 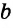 ,
, 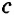 ,
, 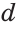 перпендикулярны одной прямой
перпендикулярны одной прямой 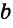 ||
|| 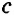 ,
, 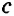 ||
|| 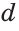 ,
, 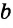 ||
|| 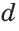 .
.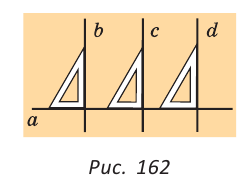
 , параллельной прямой
, параллельной прямой 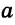 и проходящей через точку К.
и проходящей через точку К.
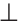
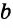 и
и 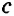
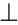
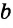 , то
, то 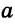 ||
|| 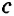 . Решение второй задачи доказывает теорему о существовании прямой, параллельной данной, которая гласит:
. Решение второй задачи доказывает теорему о существовании прямой, параллельной данной, которая гласит: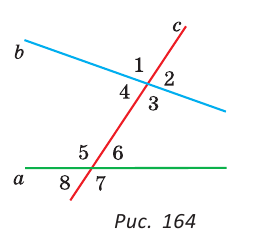
 3 и
3 и 5,
5, 4 и
4 и 6 — внутренние накрест лежащие углы;
6 — внутренние накрест лежащие углы; 2 и
2 и 8,
8, 1 и
1 и 7 — внешние накрест лежащие углы;
7 — внешние накрест лежащие углы; 6,
6, 3 и
3 и 7,
7, 1 и
1 и 5,
5, 4 и
4 и 8 — соответственные углы;
8 — соответственные углы;
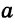 и
и 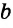 — данные прямые, АВ — секущая,
— данные прямые, АВ — секущая,  1 =
1 = 2 (рис. 166).
2 (рис. 166).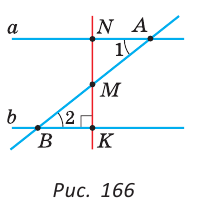
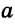 ||
||  .
.
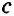 . А мы знаем, что если внутренние накрест лежащие углы равны, то прямые параллельны. Значит,
. А мы знаем, что если внутренние накрест лежащие углы равны, то прямые параллельны. Значит, 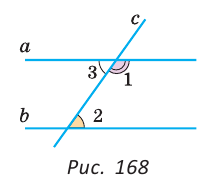
 . А мы знаем, что если внутренние накрест лежащие углы равны, то прямые параллельны. Значит,
. А мы знаем, что если внутренние накрест лежащие углы равны, то прямые параллельны. Значит, 
 AOB =
AOB =  DOC как вертикальные, ВО = ОС, АО = OD по условию). Из равенства треугольников следует, что
DOC как вертикальные, ВО = ОС, АО = OD по условию). Из равенства треугольников следует, что  BAO=
BAO= CDO. Так как эти углы — накрест лежащие при прямых АВ и CD и секущей AD, то АВ || CD по признаку параллельности прямых.
CDO. Так как эти углы — накрест лежащие при прямых АВ и CD и секущей AD, то АВ || CD по признаку параллельности прямых.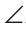 BAK = 26°,
BAK = 26°,  ADK = 128°. Доказать, что отрезок KD параллелен лучу АВ.
ADK = 128°. Доказать, что отрезок KD параллелен лучу АВ.
 BAC = 2 •
BAC = 2 • BAK = 2 • 26° = 52°.
BAK = 2 • 26° = 52°. ADK +
ADK + BAC = 128° + 52° = 180°, то KD || АВ по признаку параллельности прямых.
BAC = 128° + 52° = 180°, то KD || АВ по признаку параллельности прямых.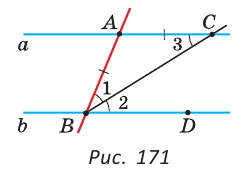
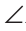 1=
1=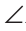 2. Так как
2. Так как  BAC равнобедренный (АВ=АС по условию), то
BAC равнобедренный (АВ=АС по условию), то 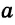 и
и 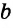 и секущей ВС. А если накрест лежащие углы равны, то прямые параллельны. Следовательно,
и секущей ВС. А если накрест лежащие углы равны, то прямые параллельны. Следовательно, 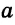 ||
||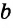 .
.

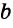 проходит через точку М и параллельна прямой
проходит через точку М и параллельна прямой 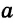 (рис. 186), то любая другая прямая, проходящая через точку М, будет пересекаться с прямой
(рис. 186), то любая другая прямая, проходящая через точку М, будет пересекаться с прямой 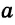 в некоторой точке, пусть и достаточно удаленной.
в некоторой точке, пусть и достаточно удаленной.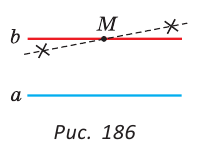
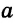 ||
||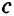 ,
, 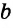 ||
|| 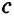 (рис. 187).
(рис. 187).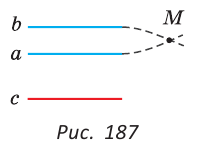
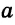 ||
||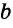 .
.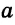 и
и 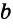 не параллельны. Тогда они пересекаются в некоторой точке М. Поэтому через точку М будут проходить две прямые
не параллельны. Тогда они пересекаются в некоторой точке М. Поэтому через точку М будут проходить две прямые 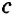 . А это противоречит аксиоме параллельных прямых. Значит, наше предположение неверно и
. А это противоречит аксиоме параллельных прямых. Значит, наше предположение неверно и  1 =
1 = 2,
2, 3 =
3 = 4. Доказать, что
4. Доказать, что 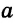 ||
|| 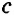 .
.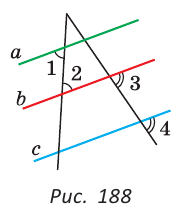
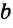 по признаку параллельности прямых. Так как соответственные углы 3 и 4 равны, то по признаку параллельности прямых
по признаку параллельности прямых. Так как соответственные углы 3 и 4 равны, то по признаку параллельности прямых  . Так как
. Так как  и
и  , то
, то 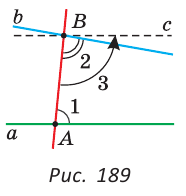
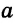 ||
|| 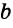 , АВ — секущая,
, АВ — секущая, 1 и
1 и 2 — внутренние накрест лежащие (рис. 195).
2 — внутренние накрест лежащие (рис. 195).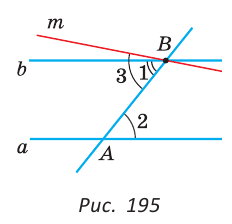
 1 =
1 = 2.
2. 1
1 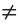
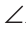 2. Отложим от луча ВА угол 3, равный углу 2. Так как внутренние накрест лежащие углы 2 и 3 равны, то
2. Отложим от луча ВА угол 3, равный углу 2. Так как внутренние накрест лежащие углы 2 и 3 равны, то 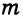 ||
|| 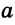 по признаку параллельности прямых. Получили, что через точку В проходят две прямые
по признаку параллельности прямых. Получили, что через точку В проходят две прямые 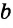 и
и 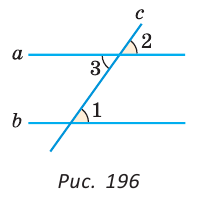
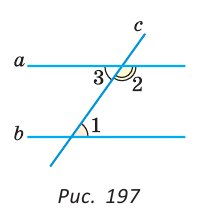
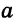 ||
|| 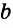 и
и 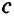
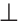
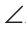 1 = 90°. Согласно следствию
1 = 90°. Согласно следствию 
 2 = 90°.
2 = 90°.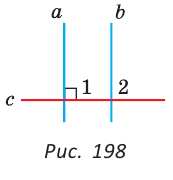
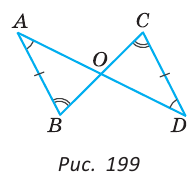
 АОВ =
АОВ = DOC по стороне и двум прилежащим к ней углам. Что и требовалось доказать.
DOC по стороне и двум прилежащим к ней углам. Что и требовалось доказать.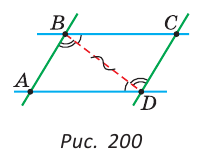
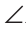 ABD =
ABD =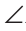 CDB как накрест лежащие при параллельных прямых АВ и CD и секущей BD,
CDB как накрест лежащие при параллельных прямых АВ и CD и секущей BD,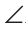 ADB =
ADB =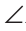 CBD как накрест лежащие при параллельных прямых ВС и AD и секущей BD. Тогда треугольники равны по стороне и двум прилежащим к ней углам. Из равенства треугольников следует, что AB=CD, BC=AD. Что и требовалось доказать.
CBD как накрест лежащие при параллельных прямых ВС и AD и секущей BD. Тогда треугольники равны по стороне и двум прилежащим к ней углам. Из равенства треугольников следует, что AB=CD, BC=AD. Что и требовалось доказать.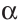 и
и 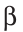 параллельны, то пишут:
параллельны, то пишут:  ||
||  (рис. 211).
(рис. 211).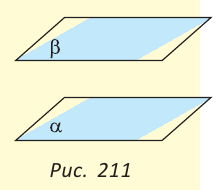
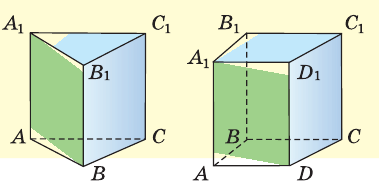
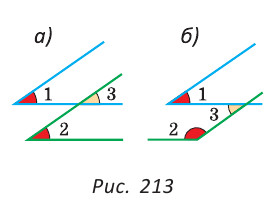
 2 =
2 = 3. Поскольку угол 1 и угол 3 дополняют угол 4 до 90°, то
3. Поскольку угол 1 и угол 3 дополняют угол 4 до 90°, то 1 =
1 = 3. Значит,
3. Значит, 1 =
1 = 2.
2.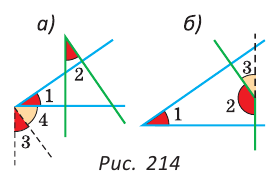
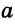 ||
|| 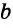 и АВ
и АВ
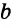 , то расстояние между прямыми
, то расстояние между прямыми 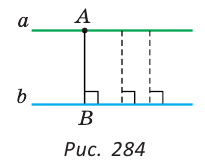
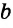 , А
, А 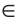
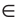
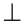
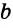 , CD
, CD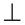
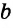 .
.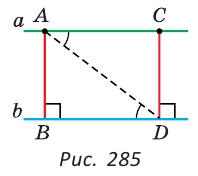
 CAD =
CAD = BDA). Откуда АВ = CD. Теорема доказана.
BDA). Откуда АВ = CD. Теорема доказана. ADC=150°. Найти расстояние между прямыми AD и ВС.
ADC=150°. Найти расстояние между прямыми AD и ВС.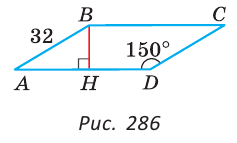
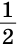 АВ = 16 см.
АВ = 16 см.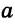 и
и 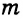 , параллельную прямой
, параллельную прямой 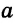 .
.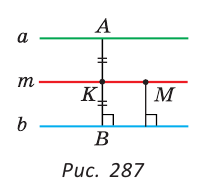
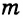 ||
|| 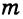 равноудалены от прямых
равноудалены от прямых 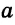 и
и 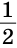 АВ.
АВ.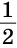 АВ. По следствию из теоремы о расстоянии между параллельными прямыми точки К и М лежат на прямой КМ, параллельной прямой
АВ. По следствию из теоремы о расстоянии между параллельными прямыми точки К и М лежат на прямой КМ, параллельной прямой 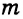 , параллельная
, параллельная  .
. равноудалены от прямых
равноудалены от прямых  . Прямая
. Прямая  , проходящая через середину общего перпендикуляра прямых
, проходящая через середину общего перпендикуляра прямых 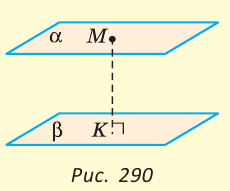
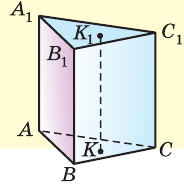
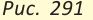
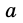 и
и 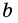 — перпендикулярные. Две прямые на плоскости называют параллельными, если они не пересекаются.
— перпендикулярные. Две прямые на плоскости называют параллельными, если они не пересекаются.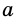 и
и 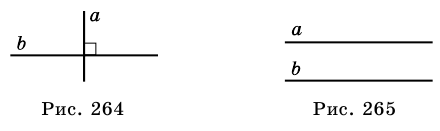
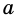 и
и 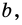 если она пересекает их в двух точках (рис. 266).
если она пересекает их в двух точках (рис. 266).