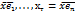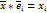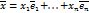Решение:
Записываем матрицу перехода А:
и находим ее определитель
0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f1 , f2 , f3 линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:
Обратная матрица А -1
Находим координаты вектора х относительно нового базиса.
Пример №1 . Даны векторы a, b, c и d . Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c
Пример №2 . Даны векторы 


Пример №3 . Даны два линейных преобразования:
х’1 = a11x1 + a12x2 + a13x3, х»1 = b11x’1 + b12x’2 + b13x’3,
х’2 = a21x1 + a22x2 + a23x3, х»2 = b21x’1 + b22x’2 + b23x’3,
х’3 = a31x1 + a32x2 + a33x3, х»3 = b31x’1 + b32x’2 + b33x’3,
Средствами матричного исчисления найти преобразование, выражающее х»1, x»2, x»3 через х1, х2, х3.
х’1 = 4x1 + 3x2 + 5x3, х»1 = — x’1 + 3x’2 — 2x’3,
х’2 = 6x1 + 7x2 + x3, х»2 = — 4x’1 + x’2 + 2x’3,
х’3 = 9x1 + x2 + 8x3, х»3 = 3x’1 — 4x’2 + 5x’3,
Решение. Используя калькулятор, получаем:
Обозначим:
| A = |
|
| B = |
|
Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .
| A -1 = -1/182 |
|
Матрицу Х ищем по формуле:
| X = A -1 ·B = -1/182 |
| * |
| = |
|
Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e 1= AB , e 2= AC , e 3= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e 1, e 2, e 3)
Решение. Пункты (а-д) решаются через онлайн калькулятор.
Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид 
Решим полученную систему уравнений.
- Координаты вектора в ортонормированном базисе
- Ортогональный и ортонормированный базисы евклидова пространства
- Выражение скалярного произведения через координаты сомножителей
- Преимущества ортонормированного базиса
- Изменение матрицы Грама при переходе от одного базиса к другому
- Свойства определителя Грама
- Изоморфизм евклидовых пространств
- 🔥 Видео
Видео:Как разложить вектор по базису - bezbotvyСкачать

Координаты вектора в ортонормированном базисе
Теорема: если ē1. ēn ортонормированный базис неравенства V
и x1. xn координаты вектора х в этом базисе, то х1=
Доказать:
69.Выражение скалярного произведения векторов и
длины вектора в ортонормированном базисе.
Если 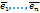
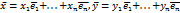
то
Доказательство: используя св-ва скалярного умножения получаем
70 Линейная независимость попарно ортогональных ненулевых векторов.
Т. Линейная независимость попарно ортогональных ненулевых век.
Док-во: ] ненул. векторы а1. аn,попарно орт. и ] イ1a1,…イnan=0
Тогда для любого i=1. n-> получаем : イ1a1•а i=0, л1•||а i||^=0 -> Т.к ||аi||не равно 0,то イi-0.
71.Существ ортонормированного базиса в вект пр-ве
Ортогонализация
Т. В любом векторном пространстве ] ортогормированного базиса
1.достаточно доказать,что существует ортогональный базис
Выбираем произволь-й базис а1. аn Прост-ва.
4. Строим е2 такой,что е2_|_е1
5. Строим е3 такой,что е3_|_е1, е3_|_е2
6. Строим еn ортогон е1,е2 и е3 и тд
7. В итоге набор попарн ортог век-ов е1,е2. еn.Доказываем что построенные век-ры ненулев.
72.Всякий ортогональный базис можно дополнить до ортогонального базиса всего пр. Док: ] W -подпр. Прост.
1. Берем в W произвол ней базис е1. еn
Дополняем его произ вольным образом до базиса е1. ек, Ак+1. Аn всего пространства
Применяемых ортогонализацию к получ. Базису пространства
Получим ортогональный базис пространств V,в . Первые K векторов образуют пространство W
73. Вект Ортогональный подпр-ву
] W подпр. прост. V.
Вектор а прост V назыв ортогональным подпр. W . если он ортогонален каждому вектору W
74 признак ортогональности век-ра подпр-ву
Т.: Пусть W – подпр-во вект. Пр-ва V, a1,…,ak-произвольный базис W.
Для того, чтобы вект а пр-ва V был ортогон-н подпр-ву W,
НИД: в-р а ортогонален каждому из в-ров а1,…,ак
Если в-р а орт. Любому в-ру из W, то он орт в-рам а1. ак
Обратно, пусть в-р а орт в-рам а1. ак. Докажем, что он орт любому в-ру из W
Рассмотрим произвольный в-р х из W. Т.к.а1. ак – базис W,
то в-р х можно представить в виде х=х1а1+..+хкак
Множ-в всех в-ров пр-ва V, орт-х подпр-ву W, обознач-ся
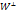
76 Т.: орт дополн-е W ⊥ подпр-ва W пр-ва V явл подпр-вом пр-ва V
1)a 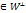
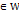
b 
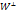

а+б
77 базис ортогонального дополнения
Т.: пусть В – вект пр-во, Р – подпр-во пр-ва В, пусть е1. ек – произв-й орт базис в Р.
Дополним его произвольным образом до ортогональн базиса всего пр-ва В: е1. ек, е(к+1). ен.
Тогда пследов-ть в-ров е(к+1). ен явл базисом пр-ва Р ⊥
78 Р – подпр-во вект пр-ва В. Тогда произв в-р а из В можно единств образом представ
в виде а=б+с, где б ∈ Р и с ∈ Р ⊥
е 1. ек – базис Р, е(к+1). ен – базис Р ⊥
а = х1е1+..+хкек + х(к+1)е(к+1)+..+хнен
78.всякий вектор пространства представить ед.обр. В виде суммы
вектора и ортогон.дополнения
Пусть W-подпр-во векторн. Прост-ва V Тогда произв.вектор а из V
можно ед.образом представить в виде a=b+c, где b прин.W;с прин.W┴
79.проекция вектора на подпространство
Для произвольн. Вектора от прост-ва V сущ. единств.представление
в виде a=b+c где b принадл.W и с принадл.W┴.Вект b наз.проекцией
вектора а на подпр-во W и обозначается prW(a)
80.Перпендикуляр короче наклонной:
пустьVвект.про-во и Wего подпр-во;bпроизв.вект.из под-ва W,
81.нахождение проекции вектора на подпр-во:
b-? Должен 1)b принадлW 2) a-b ортог.W Решение:
Условие 1 означ,что bможно выраз.через базис W
Нужно опред.коэф.для выраж.b
x1(a1*ak)+..+xk(ak*ak)=a*ak значения х надо подставить:
если a1. ak-ортог. Если ортонормир.
82.Метод наименьших квадратов.
Х-цена тов.,у-кол-во товара
нужно чтобы разница правых и левых частей была минимальной
ищем k,b так, чтобы эта величина была наименьшей
W подпр-во пр-ва R n пораждается векторами х1-хn и 11..1
ищем проекцию у1-уn на W и выражаем её через
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Ортогональный и ортонормированный базисы евклидова пространства
Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.
Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортогональным , если все образующие его векторы попарно ортогональны, т.е.
Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортонормированным , если его векторы попарно ортогональны и длина каждого из них равна единице:
Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.
В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.
Видео:Координаты в новом базисеСкачать

Выражение скалярного произведения через координаты сомножителей
Пусть [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf[/math] и [math]mathbf[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.
Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:
Преобразуем это выражение, используя операции с матрицами:
y=begin y_1&cdots& y_n end^T[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] , a [math]G(mathbf_1,mathbf_2,ldots, mathbf_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений
которая называется матрицей Грама системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] .
Видео:Координаты вектора в пространстве. 11 класс.Скачать

Преимущества ортонормированного базиса
Для ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)[/math] ортонормированной системы [math]mathbf_1, mathbf_2,ldots, mathbf_n[/math] равна единичной матрице: [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)=E[/math] .
1. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] находится по формуле: [math]langle mathbf,mathbfrangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] , а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf[/math] .
2. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] длина вектора [math]mathbf[/math] вычисляется по формуле [math]|mathbf|= sqrt[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] .
3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf[/math] относительно ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf,mathbf_1rangle,ldots, x_n=langle mathbf,mathbf_nrangle[/math] .
В самом деле, умножая обе части равенства [math]mathbf= x_1 mathbf_1+ldots+x_n mathbf_n[/math] на [math]mathbf_1[/math] , получаем
Аналогично доказываются остальные формулы.
Видео:Разложение вектора по базису. 9 класс.Скачать

Изменение матрицы Грама при переходе от одного базиса к другому
Пусть [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] и [math](mathbf)= (mathbf_1,ldots,mathbf_n)[/math] — два базиса евклидова пространства [math]mathbb[/math] , a [math]S[/math] — матрица перехода от базиса [math](mathbf)[/math] к базису [math](mathbf)colon, (mathbf)=(mathbf)S[/math] . Требуется найти связь матриц Грама систем векторов [math](mathbf)[/math] и [math](mathbf)[/math]
По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] в разных базисах:
где [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] и [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>,[/math] [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>[/math] , получаем тождество
Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :
Записав это равенство для ортонормированных базисов [math](mathbf)[/math] и [math](mathbf)[/math] , получаем [math]E=S^TES[/math] , так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf_1,ldots,mathbf_n)= G(mathbf_1,ldots,mathbf_n)=E[/math] . Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^=S^T[/math] .
Видео:Координаты точки и координаты вектора 1.Скачать

Свойства определителя Грама
Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.
1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.
Действительно, если система [math]mathbf_1, mathbf_2, ldots,mathbf_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math] , не равные нулю одновременно, что
Умножая это равенство скалярно на [math]mathbf_1[/math] , затем на [math]mathbf_2[/math] и т.д. на [math]mathbf_k[/math] , получаем однородную систему уравнений [math]G(mathbf_1,mathbf_2,ldots,mathbf_k)x=o[/math] , которая имеет нетривиальное решение [math]x=beginx_1&cdots&x_k end^T[/math] . Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.
Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.
Главный минор матрицы Грама системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.
2. Определитель Грама [math]det<G (mathbf_1,mathbf_2, ldots, mathbf_k)>[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] . Другими словами, если в процессе ортогонализации векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] получены векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , то
Действительно, в процессе ортогонализации по векторам [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] последовательно строятся векторы
После первого шага определитель Грама не изменяется
Выполним с определителем [math]det G(mathbf_1, mathbf_2, ldots,mathbf_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_)[/math] , а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_)[/math] . Получим определитель
Так как при этих преобразованиях определитель не изменяется, то
Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:
Вычислим правую часть этого равенства. Матрица [math]G(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] Грама ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов является диагональной, так как [math]langle mathbf_i,mathbf_jrangle=0[/math] при [math]ine j[/math] . Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:
3. Определитель Грама любой системы [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] векторов удовлетворяет двойному неравенству
Докажем неотрицательность определителя Грама. Если система [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , для которых по свойству 2:
Оценим теперь скалярный квадрат [math]langle mathbf_j,mathbf_jrangle[/math] . Выполняя процесс ортого-1нализации, имеем [math]mathbf_j= mathbf_j+ alpha_mathbf_1+ ldots+ alpha_mathbf_[/math] . Отсюда
Следовательно, по свойству 2 имеем
1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.
2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.
3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара :
Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math] , элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math] . Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb^n[/math] . По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:
4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Изоморфизм евклидовых пространств
Два евклидовых пространства [math]mathbb[/math] и [math]mathbb'[/math] называются изоморфными [math](mathbbleftrightarrow mathbb’)[/math] , если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:
где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb[/math] и [math]mathbb'[/math] соответственно.
Напомним, что для изоморфизма конечномерных линейных пространств необходимо и достаточно, чтобы их размерности совпадали (см. теорему 8.3). Покажем, что это условие достаточно для изоморфизма евклидовых пространств (необходимость следует из определения). Как и при доказательстве теоремы 8.3, установим изоморфизм n-мерного евклидова пространства [math]mathbb[/math] с вещественным арифметическим пространством [math]mathbb^n[/math] со скалярным произведением (8.27). В самом деле, взяв в пространстве [math]mathbb[/math] какой-нибудь ортонормированный базис [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] , поставим в соответствие каждому вектору [math]mathbfin mathbb[/math] его координатный столбец [math]xin mathbb^n
(mathbfleftrightarrow x)[/math] . Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbbleftrightarrow mathbb^n[/math] . В ортонормированном базисе скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] пространства [math]mathbb[/math] находится по формуле
(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math] , т.е. скалярные произведения соответствующих элементов равны
Следовательно, евклидовы пространства [math]mathbb[/math] и [math]mathbb^n[/math] изоморфны.
Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb^n[/math] со стандартным скалярным произведением (8.27).
🔥 Видео
Координаты вектора. 9 класс.Скачать

Базис. Разложение вектора по базису.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Вывод формулы скалярного произведения векторов, заданных координатами в ортонормированном базисе.Скачать

Найдите разложение вектора по векторам (базису)Скачать

Образуют ли данные векторы базисСкачать

Как найти координаты вектора?Скачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Замена базиса. ТемаСкачать

§48 Ортонормированный базис евклидова пространстваСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Матрица переходаСкачать