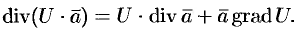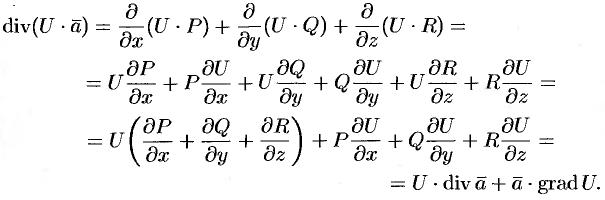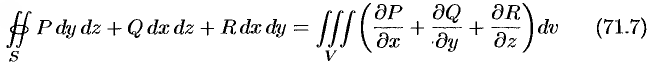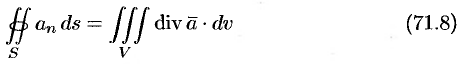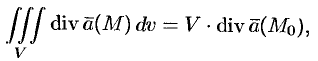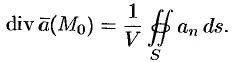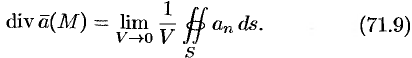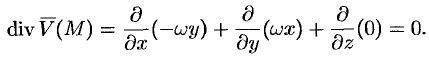В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
- Примеры: базовые понятия теории поля
- Поток поля через поверхность
- Циркуляция векторного поля
- Работа векторного поля
- Типовой расчет по теории поля
- Помощь с решением заданий
- Основные операции векторного анализа в криволинейных координатах
- В цилиндрических координатах или в сферических координатах
- Дивергенция в ортогональных координатах
- Дивергенция поля. Формула Остроградского-Гаусса
- Дивергенция поля. Формула Остроградского-Гаусса
- Пример №71.4.
- 📸 Видео
Видео:Найти дивергенцию и ротор векторного поляСкачать

Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline=(3x-y) overline+(6z+5x) overline$
Задача 4. Вычислить потенциальную функцию векторного поля
Видео:ДивергенцияСкачать

Поток поля через поверхность
Видео:Дивергенция векторного поляСкачать

Циркуляция векторного поля
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ overline = (3x-1) overline+ (y-x+z)overline+4z overline, $$ $L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Видео:Ротор векторного поляСкачать

Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline = xz overline -overline+y overline$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Видео:Демидович №4427: дивергенция радиус-вектораСкачать

Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline = z overline+ (x+y)overline+y overline, quad (p): 2x+y+2z=2. $$
Видео:#8 Ротор/Дивергенция/ГрадиентСкачать

Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.
Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Основные операции векторного анализа в криволинейных координатах
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Дифференциальные уравнения векторных линий Рассмотрим поле вектора Уравнения векторных линий в криволинейных координатах q, q2i g3 имеют вид В цилиндрических координатах в сферических координатах 14.2. Градиент в ортогональных координатах Пусть скалярное поле. Тогда Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах Дивергенция в ортогональных координатах.
Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах Оператор Лапласа в ортогональных координатах В цилиндрических координатах в сферических координатах 14.3. Ротор в ортогональных координатах Рассмотрим векгорное поле и вычислим rot а. Имеем В цилиндрических координатах в сферических координатах 14.4. Дивергенция в ортогональных координатах Дивергенция div а векторного поля вычисляется по формуле.
В цилиндрических координатах или в сферических координатах
Применяя формулу (7) к единичным векторам получим Вычисление потока в криволинейных координатах Пусть S — часть координатной поверхности , ограниченная координатными линиями Тогда поток вектора через поверхность 5 в направлении вектора ei вычисляется по формуле Аналогично вычисляется поток через часть поверхности д2 = с, а также через часть поверхности д3 = с, где с = const. Пример I.
Найти поток П векторного поля через внешнюю сторону верхней полусферы 5 радиуса R с центром в начале координат. Ч Полусфера S есть часть юординатной поверхности г = const, а именно г = R. На полусфере 5 имеем , причем Учитывая, что в сферических коорои патах по формуле (8) найдем 14.6. Вычисление потенциала в криволинейных координатах Пусть в некоторой области О задано потенциальное векторное поле в области Для нахождения потенциала ) этого векторного поля запишем равенство в следующем виде:
Отсюда следует, что Интегрируя систему дифференциальных уравнений с частными производными (9), найдем искомый потенциал произвольная постоянная. В цилиндрических координатах система (9) принимает вид В сферических координатах система (9) имеет вид Пример 2. Найти потенциал векторного поля, заданного в цилиндрических координа тех Убедимся, что По формуле (5) л о лучим данное поле потенциально.
Искомый потенциал и = и(р, у, г) является решением следующей системы дифференциальных уравнений с частными производными (см. формулу (10)): Интегрированием по р из первого уравнения находим Дифференцируя соотношение (11) no р и используя второе уравнение, получим или откуда . Таким образом.
Возможно вам будут полезны данные страницы:
Дифференцируя это соотношение no z и используя тре тье уравнение, получим Линейный интеграл и циркуляция в ортогональных криволинейных координатах Пусть векторное поле определено и непрерывно в области Q изменения ортогональных криволинейных координат 4i, 42, 4з • Так как дифференциал радиус-вектора г любой точки M(qb 42, 43) G П выражается формулой то криволинейный интеграл вектора а(М) по ориентированной гладкой или кусочно-гладкой кривой L СП будет равен В частности, для цилиндрических координат ) будем иметь.
Отсюда по формуле (13) получим Аналогично для сферических координат будем иметь Отсюда по формуле (13) получим Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах Дивергенция в ортогональных координатах.
Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах.
Оператор Лапласа в ортогональных координатах Если кривая L замкнута (начальная и конечная точки кривой L совпадают), то циркуляция Ц векторного поля а(М) в криволинейных координатах 4,, q2, 43 вычисляется по формуле (13), а в случае цилиндрических или сферических координат — по формулам (14) или (15) соответственно. Пример 3. Вычислить циркуляцию векторного поля, заданного в цилиндрических координатах по замкнутой кривой L, Координаты данного вектора равны соответственно Контур L представляет собой замкнутую кривую, расположенную в плоскости z = 0 (рис. 43).
Подставляя координаты данного вектора в формулу.(14), получим На кривой L имеем . Искомая циркуляция будет равна 14.8. Оператор Лапласа в ортогональных координатах Если скалярная функция, то Используя формулы (16) и (17), для оператора Лапласа Д получим следующее выражение В цилиндрических координатах получим В сферических координатах будем иметь Пример 4. Найти все решения уравнения Лапласа Аи = 0, зависящие только от расстояния г.
Так как искомое решение и должно зависеть только от расстояния точки М от начала координат г, т., то уравнение Лапласа Ди = 0 в сферических координатах будет иметь вид Отсюда так что где постоянные. Упражнения Найдите производную скалярного поля в точке по направлению кточке Найдите производную скалярного поля и(х, у, z) в точке Л#о(хо, Уо» *о) по направлению нормали к поверхности S, образующей острый угол с положительным направлением оси О г: 6.
Найдите производную скалярного поля в точке эллипса + = 1 по направлению внешней нормали к эллипсу в этой точке. 7. Найдите производную скалярного поля в точке по направлению окружности 8. Найдигеугол между градиентами функции и = arctg | в точках 9. Найдите производную плоского поля и вточке понаправле-нию, задаваемому вектором, лежащим в плоскости хОу и наклоненным под углом | коси Ох. Найдите векторные линии следующих векторных полей: 13.
| Найдите векторную линию поля а , проходящую |
через точку 14. Найдите векгорную линию поля а, проходящую через точку М(3,4, -1). 15. Вычислите поток векторного поля через верхнюю сторону круга, вырезаемого конусом х2 4- у2 = г2 из плоскости 16. Вычислите поток векторного поля к через треугольник ABC с вершинами в точках (нормаль образует с осью Oz острый угол). 17. Вычислите поток векторного поля а = xi + zk через боковую поверхность кругового цилиндра , ограниченную плоскостями z 18.
Вычислите поток векторного поля а = yzi — xj — yk через полную поверхность конуса х2 + у2 = z2, ограниченную плоскостью z Методом введения криволинейных координат на поверхности вычислите поток заданного векгора а через заданную поверхность S: 19. — внешняя сторона цилиндрической поверхности х2 + у2 = 9, ограниченной сферой Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах.
Дивергенция в ортогональных координатах
Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах Оператор Лапласа в ортогональных координатах 20. — внешняя сторона части сферы , вырезанная конической поверхностью Вычислите поток векгорного поля а через замкнутую поверхность S (нормаль внешняя). Проверьте результат с помощью формулы Гаусса—Остроградского:
Достраивая подходящим образом заданные незамкнутые поверхности до замкнутых и пользуясь теоремой Гаусса—Остроградского, вычислите потоки векторных полей через указанные поверхности (к замкнутой поверхности берем внешнюю нормаль): Найдите работу силы F при перемещении вдольлинии L от точки М к точке N: Найдите циркуляцию векторного поля а вдоль замкнутого контура L (в направлении, соответствующем возрастанию параметра Вычислите циркуляцию векторного поля а по замкнутому контуру L.
Проверьте результат при помощи формулы Стокса: — линия пересечения плоскости с координатными плоскостями 38. Найдите дивергенцию векторного пол я а = (с, г), где с — постоянный вектор, . 39. При какой функции ip(z) дивергенция векгорного поля а =)k будет равна z? 40. Найдите , где г = 41. Найдите функцию tf>(r), для которой выполняется равенство 42. Какова должна быть функция /(х, z), чтобы ротор векгорного поля совпал с вектором Найдите ротор следующих векторов: Докажите, что следующие векторные поля являются потенциальными, и найдите их потенциалы: Ответы
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Поток векторного поля через замкнутую поверхностьСкачать

Дивергенция поля. Формула Остроградского-Гаусса
Дивергенция поля. Формула Остроградского-Гаусса
Важной характеристикой векторного поля (71.1) является так называемая дивергенция, характеризующая распределение и интенсивность источников и стоков поля.
Дивергенцией (или расходимостью) векторного поля
в точке 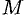
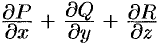
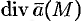
Отметим некоторые свойства дивергенции.
- Если
— постоянный вектор, то
.
, где
.
, т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
- Если
— скалярная функция,
— вектор, то
Эти свойства легко проверить, используя формулу (71.6). Докажем, например, справедливость свойства 4.
Так как 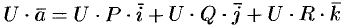
Используя понятия потока и дивергенции векторного поля, запишем известную в анализе (см. (58.9)) формулу Остроградского Гаусса
в так называемой векторной форме.
Рассматривая область 




(в котором она чаще всего и встречается).
Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность 

Используя формулу (71.8), можно дать другое определение дивергенции векторного поля 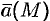
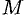
По теореме о среднем для тройного интеграла (см. п. 54.1) имеем:
где 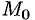

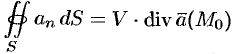
Пусть поверхность 
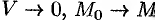
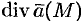

Дивергенцией векторного поля в точке 


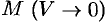
Определение (71.9) дивергенции эквивалентно (можно показать) определению (71.6).
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.
Исходя из физического смысла потока (обычно условно считают; что 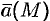
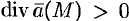

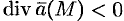

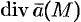

Понятно, что если в объеме 

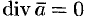
Векторное поле, в каждой точке которого дивергенция поля равна нулю, т. е. 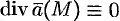
Пример №71.4.
Найти дивергенцию поля линейных скоростей 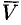
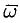
Решение:
Примем ось вращения жидкости за ось 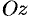
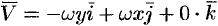
Поле 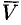
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📸 Видео
Координаты вектора. 9 класс.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

ДИВЕРГЕНЦИЯ и РОТОР векторного поляСкачать

РоторСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Координаты вектора в пространстве. 11 класс.Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Найти дивергенцию градиента функции f(r)Скачать

ДивергенцияСкачать

Найдите разложение вектора по векторам (базису)Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать












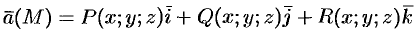
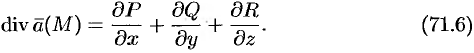
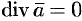 .
.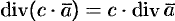 , где
, где 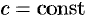 .
.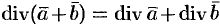 , т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
, т. e. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых. — скалярная функция,
— скалярная функция,