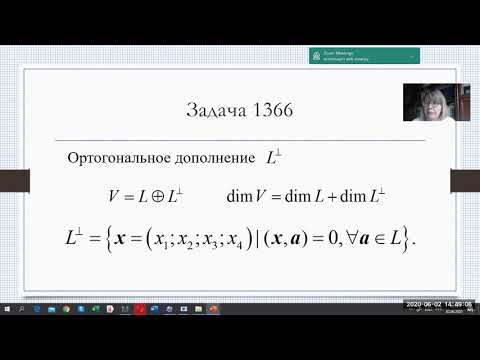
Ортогональным дополнением непустого подмножества [math]M[/math] евклидова пространства [math]mathbb[/math] называется множество векторов, ортогональных каждому вектору из [math]M[/math] . Ортогональное дополнение обозначается
forall mathbfin M Bigr>.[/math]
Рассмотрим примеры ортогональных дополнений евклидова пространства.
1. Ортогональным дополнением нулевого подпространства [math] <mathbf> triangleleft mathbb[/math] служит все пространство [math]mathbb colon, <mathbf>^= mathbb[/math] . Ортогональным дополнением всего пространства является его нулевое подпространство [math]mathbb^= <mathbf>[/math] .
2. Пусть в пространстве [math][/math] радиус-векторов (с началом в точке [math]O[/math] ) за даны три взаимно перпендикулярных радиус-вектора [math]overrightarrow[/math] , [math]overrightarrow[/math] и [math]overrightarrow[/math] . Тогда ортогональным дополнением вектора [math]overrightarrow[/math] является множество радиус- векторов на плоскости, содержащей векторы [math]overrightarrow[/math] и [math]overrightarrow[/math] , точнее, [math]<overrightarrow>^= operatorname(overrightarrow,overrightarrow)[/math] . Ортогональным дополнением векторов [math]overrightarrow[/math] и [math]overrightarrow[/math] служит множество радиус-векторов на прямой, содержащей вектор [math]overrightarrowcolon <overrightarrow,overrightarrow>^= operatorname (overrightarrow)[/math] . Ортогональным дополнение трех заданных векторов служит нулевой радиус-вектор: [math]<overrightarrow, overrightarrow, overrightarrow>^= <overrightarrow>[/math] .
3. В пространстве [math]P_2(mathbb)[/math] многочленов степени не выше второй со скалярным произведением (8.29) задано подмножество [math]P_0(mathbb)[/math] — многочленов нулевой степени. Найдем ортогональное дополнение этого подмножества. Для этого приравняем нулю скалярное произведение многочлена [math]p_2(x)=ax^2+bx+c[/math] на постоянный многочлен [math]p_0(x)=dcolon[/math] [math]langle p_2(x),p_0(x)rangle= acdot0+bcdot0+ccdot d=0[/math] . Поскольку величина [math]d[/math] произвольная, то [math]c=0[/math] . Следовательно, ортогональным дополнением подмножества [math]P_0(mathbb)[/math] является множество многочленов из [math]P_0(mathbb)[/math] с нулевым свободным членом.
Видео:Как разложить вектор по базису - bezbotvyСкачать

Свойства ортогонального дополнения
Рассмотрим свойства ортогональных дополнений подмножеств n-мерного евклидова пространства [math]mathbb[/math] .
1. Ортогональное дополнение [math]M^[/math] непустого подмножества [math]Msubset mathbb[/math] является линейным подпространством, т.е. [math]M^ triangleleft mathbb[/math] , и справедливо включение [math]Msubset (M^)^[/math] .
В самом деле, множество [math]M^[/math] замкнуто по отношению к операциям сложения векторов и умножения вектора на число, так как сумма двух век торов, ортогональных [math]M[/math] , ортогональна [math]M[/math] , и произведение вектора, ортогонального [math]M[/math] , на любое число является вектором, ортогональным [math]M[/math] . До кажем включение [math]Msubset (M^)^[/math] . Пусть [math]mathbfin M[/math] , тогда [math]langle mathbf,mathbfrangle=0[/math] для любого вектора [math]mathbfin M^[/math] . Но это означает, что [math]mathbfsubset (M^)^[/math] .
2. Пересечение любого непустого подмножества [math]Msubset mathbb[/math] со своим ортогональным дополнением есть нулевой вектор: [math]Mcap M^= <mathbf>[/math] .
Действительно, только нулевой вектор ортогонален самому себе.
3. Если [math]L[/math] — подпространство [math]mathbb
(Ltriangleleft mathbb)[/math] , то [math]mathbb=Loplus L^[/math] .
Действительно, возьмем в [math]L[/math] ортогональный базис [math](mathbf)= (mathbf_1, ldots,mathbf_k)[/math] . До полним его векторами [math](mathbf)= (mathbf_,ldots, mathbf_n)[/math] до ортогонального базиса [math](mathbf),,(mathbf)[/math] всего пространства [math]mathbb[/math] . Тогда произвольный вектор [math]mathbfin mathbb[/math] можно представить в виде суммы
где [math]mathbfin L[/math] , а [math]mathbfin L^[/math] , так как [math]langle mathbf,mathbf_irangle= sum_^mathbflangle mathbf_j, mathbf_i rangle_<_>=0[/math] для [math]i=1,ldots,k[/math] . Следовательно, любой вектор пространства [math]mathbb[/math] раскладывается по подпространствам [math]L[/math] и [math]L^[/math] , т.е. [math]mathbb= L+L^[/math] . Эта алгебраическая сумма является прямой суммой по свойству 2, поскольку [math]Lcap L^=<mathbf>[/math] . Следовательно, [math]mathbb=Loplus L^[/math] .
4. Если [math]Ltriangleleft mathbb[/math] , то [math]dim<L^>= dimmathbb-dim[/math] .
5. Если [math]L[/math] — подпространство [math]mathbb[/math] , то [math]L=(L^)^[/math] .
Из первого свойства следует включение [math]Lsubset(L^)^[/math] . Докажем, что [math](L^)^subset L[/math] . Действительно, пусть [math]mathbfin (L^)^[/math] . По свойству 3: [math]mathbf=mathbf+mathbf[/math] , где [math]mathbfin L,
mathbfin L^[/math] . Найдем скалярное произведение
Следовательно, [math]langle mathbf,mathbfrangle=0[/math] , и согласно аксиоме 4 скалярного произведения [math]mathbf=mathbf[/math] , поэтому [math]mathbf=mathbf+ mathbf= mathbf+mathbf=mathbfin L[/math] . Значит, [math](L^)^subset L[/math] . Из двух включений [math]Lsubset (L^)^[/math] и [math](L^)^ subset L[/math] следует равенство [math]L=(L^)^[/math] .
6. Если [math]L_1triangleleft mathbb[/math] и [math]L_2triangleleft mathbb[/math] , то [math](L_1+L_2)^=L_1^cap L_2^[/math] и [math](L_1cap L_2)^= L_1^+ L_2^[/math] .
Последние свойства аналогичны свойствам алгебраических дополнений.
Видео:Линейная оболочка. Базис и размерностьСкачать

Нахождение ортогонального дополнения подпространства
Ранее для описания подпространств линейных пространств использовались два способа описания (внешний и внутренний). Рассмотрим применение этих способов описания для нахождения ортогональных дополнений подпространств. Учитывая изоморфизм евклидовых пространств, будем рассматривать арифметическое пространство [math]mathbb^n[/math] со скалярным произведением (8.27).
Для заданного подпространства [math]Ltriangleleft mathbb^n[/math] требуется найти его ортогональное дополнение [math]L^[/math] . В зависимости от способа описания подпространства [math]L[/math] используем одно из следующих двух утверждений.
1. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как линейная оболочка [math]L=operatorname(a_1,ldots,a_k)[/math] столбцов матрицы [math]A= begina_1&cdots&a_kend[/math] , то множество решений однородной системы [math]Ax=o[/math] является его ортогональным дополнением [math]L^triangleleft mathbb^n[/math] , т.е.
2. Если подпространство [math]Ltriangleleft mathbb^n[/math] задано как множество решений однородной системы [math]Ax=o[/math] [math]m[/math] уравнений с [math]n[/math] неизвестными, то линейная оболочка столбцов [math]a_1^T,ldots,a_m^T[/math] транспонированной матрицы [math]A^T=begina_1^T&cdots&a_m^Tend[/math] является его ортогональным дополнением [math]L^triangleleft mathbb^n[/math] , т.е.
где [math]a_i^T[/math] — i-й столбец матрицы [math]A^T[/math] .
Докажем, например, первое утверждение. Линейное однородное уравнение
1. В отличие от алгебраического дополнения [math]L^[/math] подпространстве [math]Ltriangleleft mathbb[/math] ортогональное дополнение [math]L^[/math] находится однозначно.
2. Ортогональное дополнение [math]L^[/math] подпространства [math]Ltriangleleft mathbb[/math] в силу свойства 3 является также и алгебраическим дополнением. Это обстоятельстве учитывалось при нахождении алгебраических дополнений при помощи утверждений (8.16) и (8.17), которые по существу совпадают с утверждениями (8.34) и (8.35).
Пример 8.19. В примере 8.10 для линейного подпространства [math]L= operatorname[(t-1)^2,(t+1)^3][/math] пространства [math]P_3(mathbb)[/math] многочленов не более, чем 3-й степени, было найдено алгебраическое дополнение
Доказать, что это алгебраическое дополнение является ортогональным дополнением подпространства [math]L[/math] евклидова пространства [math]P_3(mathbb)[/math] со скалярным произведением (8.29).
Решение. Для решения задачи достаточно показать, что образующие подпространства [math]L:[/math]
ортогональны образующим алгебраического дополнения [math]L^:[/math]
Видео:Ортогональное дополнение. ПримерСкачать

Найти базис в ортогональном дополнении к линейной оболочке векторов
Задачи по алгебре. Выпуск 2.
Задача 1. Найти 5А, если
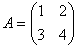
Задача 2. Найти А +В, если
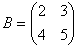
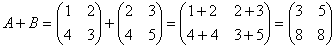
Задача 3. Найти АВ , если
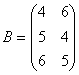
Задача 4. Найти транспонированную матрицу относительно матрицы
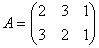
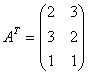
Задача 5. Найти 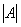
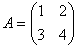
Задача 6. Найти 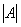
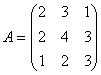
Задача 7. Вычислить определитель
Решение: Разложим определитель по первой строке:
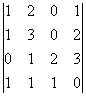
Задача 8. Найти обратную матрицу для матрицы
Определитель нулю не равен, следовательно, обратная матрица существует. Найдем алгебраические дополнения (знаки их учтем сразу), т. е.
Мы сами можем проверить результат, Известно, что 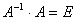
Получилась единичная матрица. Значит, обратная матрица найдена верно.
Задача 9. Решить систему матричным способом:
Не является ли матрица А вырожденной? Найдем ее определитель: det А =1•[-1•4 – 1•2] – 1•[2•4 – 2•4] + 2•[2•1 – 4•(-1)] = -6 + 12 = 6
Определитель не равен нулю, то есть матрица не вырожденная. Значит, существует обратная матрица
Можно убедиться проверкой в правильности решения: подставим вектор Х в первоначальное матричное уравнение.
Действительно вектор Х удовлетворяет заданной системе.
Задача 10. Решить систему с помощью формул Крамера :
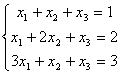
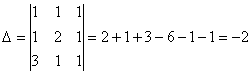
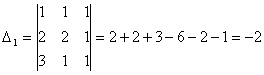
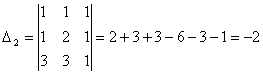
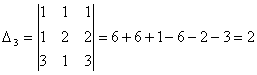
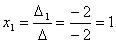
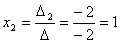
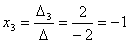
Задача 11. Вычислить :
Раскроем скобки и получим:
Так как 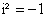
Задача 12. Вычислить, пользуясь формулой Муавра:
Представим число z в тригонометрической форме.
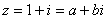
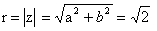
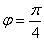
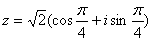
Применим формулу Муавра:
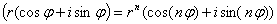
Задача 13. Выполнить деление с остатком f ( x )= x 3 — x 2 — x на x -1+2 i .
Решение: Составим таблицу, в которой над чертой расположены коэффициенты многочлена f ( x ), под чертой соответствующие коэффициенты частного и остаток, последовательно вычисляемые, а слева сбоку – значение c = 1-2 i в данном примере.
Таким образом: f ( x )= x 3 — x 2 — x =( x -1+2 i ) ( x 2 -2 ix -5-2 i )-9+8 i .
Ответ : f(x)=x 3 -x 2 -x=(x-1+2i) (x 2 -2ix-5-2i)-9+8i.
Задача 14. Применяя процесс ортогонализации, построить ортогональный базис подпространства, натянутого на данную систему векторов.
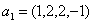
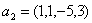
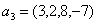
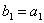
Задача 15. Проверить, что векторы х = (1, -2, 2, -3), у = (2, -3, 2, 4) ортогональны, и дополнить их до ортогональных базисов.
Решение: Найдем скалярное произведение данных векторов: ( х , у) = 2+6+4-12 = 0 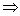
Найдем векторы, дополняющие данную систему векторов до ортогонального базиса.
Пусть z = (z1, z2, z 3, z 4) попарно ортогонален с данными векторами, т.е. ( x , z ) = 0 и ( y , z ) = 0. Получаем следующую систему:
Эта система имеет множество решений, например,
Пусть теперь k = ( k 1, k 2, k 3, k 4) попарно ортогонален с векторами x , y , z . Получаем следующую систему:
Эта система имеет множество решений, например,
Таким образом, можно добавить векторы
(2, 2, 1, 0), (-5, 2, 6, 1).
Задача 16. Найти векторы, дополняющие следующую систему векторов 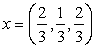
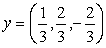
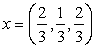
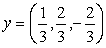
Пусть z = (z1, z2, z 3) попарно ортогонален с данными векторами, т.е. ( x , z ) = 0 и ( y , z ) = 0. Получаем следующую систему:
Эта система имеет множество решений, например,
Нормируя этот вектор, получим вектор, дополняющий данную систему векторов до ортонормированного базиса:
Задача 17. Доказать, что проектирование трехмерного пространства на координатную плоскость натянутую на вектора e 1, e 2 параллельно оси координат вектора e 3, является линейным преобразованием, и найти его матрицу в базисе e 1, e 2, e 3..
Решение: Пусть L — трёхмерное пространство, e 1, e 2, e 3 — базис L , преобразование 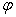
Пусть х — произвольный вектор L , т.е. x Î L .
Пусть x =( x 1, x 2, x 3) — координаты вектора x в базисе e 1, e 2, e 3, т.е. x = x 1 e 1+ x 2 e 2+ x 3 e 3. Тогда при преобразовании j имеем:
Докажем, что для любых x Î L , y Î L и числа l
1) j ( x+y )= j (x)+ j (y),
2) j ( l x )= l j (x).
j ( l x ) = ( l x 1, l x 2, 0) = l ( x 1, x 2, 0) = l j ( x ) .
Следовательно, j — линейное преобразование.
Найдем матрицу преобразования j в базисе e 1, e 2, e 3. Известно, что координаты образа j ( x ) вектора x при линейном преобразовании выражаются через координаты вектора x в том же базисе при помощи матрицы преобразования A j следующим образом:
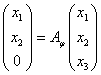
Откуда следует, что
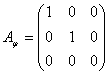
Задача 18. Линейное преобразование φ в базисе е 1 , е2, е3, е4 имеет матрицу
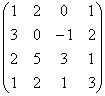
Выпишем матрицу перехода от базиса е 1 ,е2,е3,е4 к новому базису:
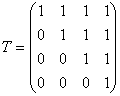
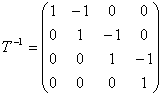
Теперь найдем матрицу преобразования В j в новом базисе по формуле В j =Т -1 А j Т.
Задача 19. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:
Решение: Собственные значения являются корнями характеристического уравнения преобразования j .
Составим характеристическую матрицу:
Найдем определитель матрицы и вычислим корни характеристического уравнения:
= (2 — 




= 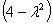
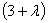


= 12+4 
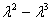

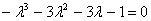
Получим собственные значения: 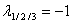
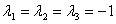
Для каждого собственного значения найдем собственный вектор.
По определению имеем: 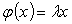
Но, в тоже время,
Беря значением 
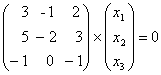

Собственными векторами будут являться вектора, входящие в фундаментальную систему решений (ф.с.р.) этой с.л.а .у . Найдем ф.с.р. это с.л.а .у .
Таким образом, собственным вектором, отвечающим собственному значению 
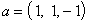
Задача 20. Найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду, для следующей квадратичной формы: 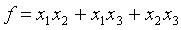
Решение: Ввиду отсутствия в этой форме квадратов неизвестных мы выполним сначала невырожденное линейное преобразование:
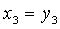
после чего получим 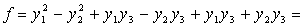
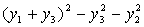
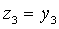
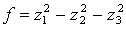
Найдем невырожденное линейное преобразование.
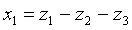
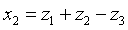
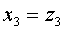
Задача 21. Следующую квадратичную форму привести к каноническому виду с целыми коэффициентами посредством невырожденного линейного преобразования с рациональными коэффициентами и найти выражение новых неизвестных через старые.
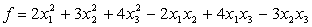
Решение: Приведем данную форму к каноническому виду:
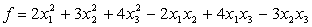
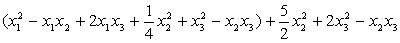
= 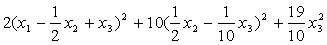
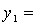
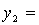
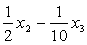
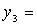
получим канонический вид квадратичной формы:
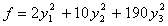
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Учебное пособие: Методические указания для студентов 1 курса Одесса 2008
| Название: Методические указания для студентов 1 курса Одесса 2008 Раздел: Остальные рефераты Тип: учебное пособие Добавлен 17:40:19 17 сентября 2011 Похожие работы Просмотров: 2273 Комментариев: 8 Оценило: 1 человек Средний балл: 2 Оценка: неизвестно Скачать |
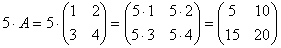
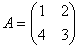
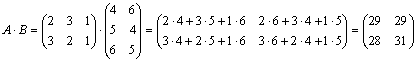
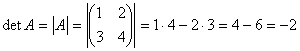
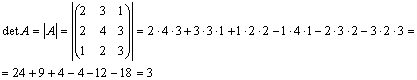
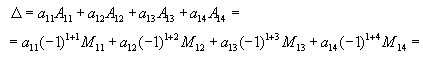
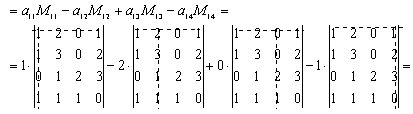
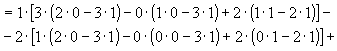
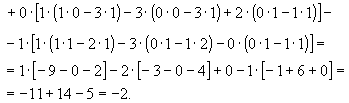
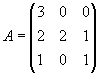
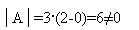
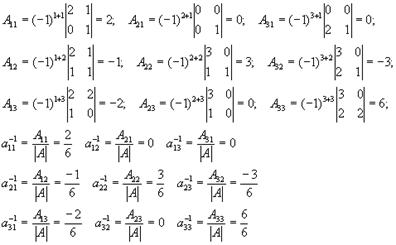
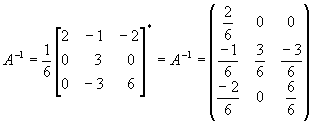
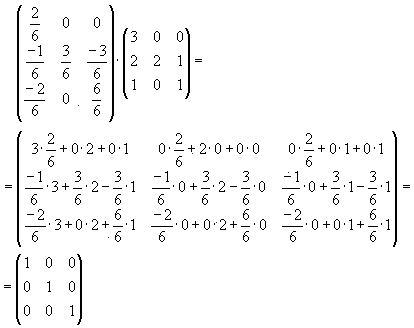
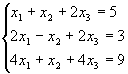
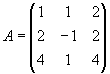
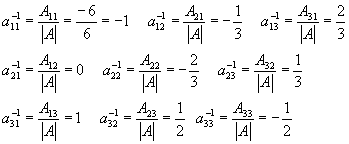
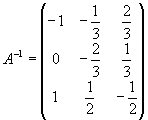
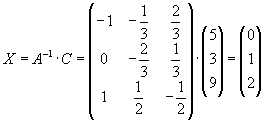
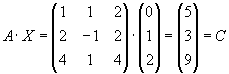
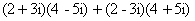
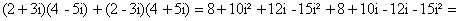
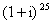
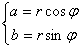
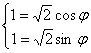
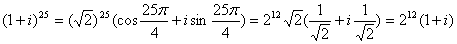
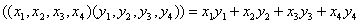
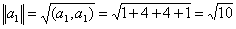
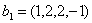
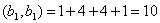
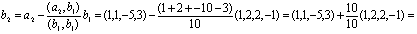
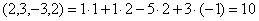
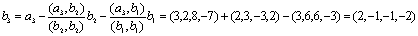
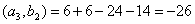
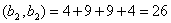
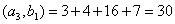
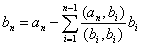
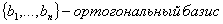
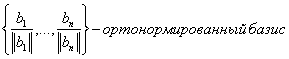
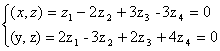
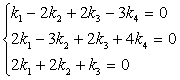
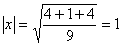
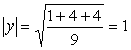
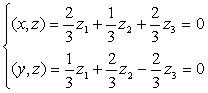
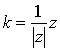
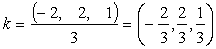
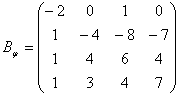
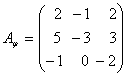
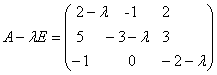
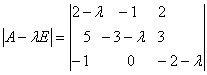
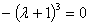
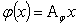
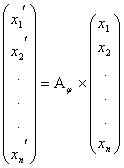
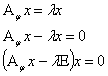
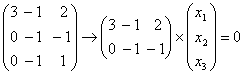
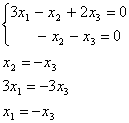
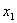
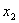
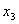
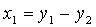
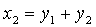
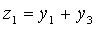
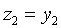
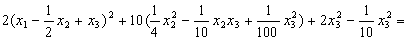
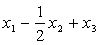
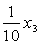
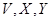 — произвольные пространства над некоторым полем
— произвольные пространства над некоторым полем 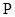 ;
;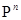 — пространство
— пространство 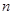 — мерных строк (столбцов) с элементами из поля
— мерных строк (столбцов) с элементами из поля 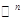 — действительное
— действительное 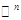 — комплексное
— комплексное 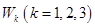 — пространства геометрических векторов (прямой, плоскости, пространства);
— пространства геометрических векторов (прямой, плоскости, пространства);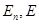 — евклидовы пространства (с указанием размерности или без него);
— евклидовы пространства (с указанием размерности или без него);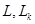 — подпространства данного пространства (
— подпространства данного пространства (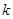 — индекс, не связанный с размерностью);
— индекс, не связанный с размерностью);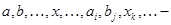 векторы рассматриваемого пространства;
векторы рассматриваемого пространства; 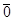 — нулевой вектор;
— нулевой вектор;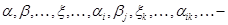 скаляры из данного поля,
скаляры из данного поля,  — нуль этого поля;
— нуль этого поля;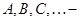 линейные операторы, в отдельных случаях – матрицы;
линейные операторы, в отдельных случаях – матрицы;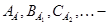 матрицы линейных операторов в базисах соответственно
матрицы линейных операторов в базисах соответственно 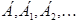 ;
;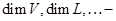 размерности пространств
размерности пространств 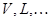 ;
;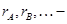 ранги операторов (матриц)
ранги операторов (матриц) 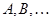 ;
;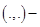 скалярное произведение в данном пространстве;
скалярное произведение в данном пространстве;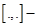 векторное произведение в данном пространстве
векторное произведение в данном пространстве 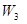 .
.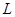 векторов пространства
векторов пространства 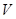 над полем
над полем 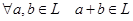 ,
,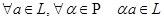 .
.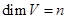 , а
, а 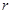 условий специального вида, то есть основания ожидать, что
условий специального вида, то есть основания ожидать, что 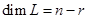 .
.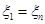 , поэтому
, поэтому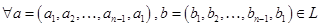
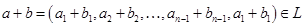 ,
,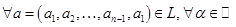
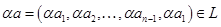 .
.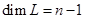 . Для этого рассмотрим векторы стандартного базиса
. Для этого рассмотрим векторы стандартного базиса 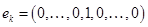
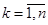 . Векторы
. Векторы 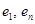 не принадлежат
не принадлежат 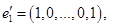
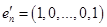 . Рассмотрим систему векторов
. Рассмотрим систему векторов 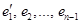 . Она образует базис
. Она образует базис 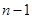 , то и
, то и 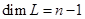 . Итак, наше предположение оказалось верным.
. Итак, наше предположение оказалось верным.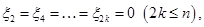 поэтому следует ожидать, что
поэтому следует ожидать, что 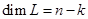 , где
, где 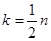 , если
, если 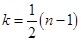 , если
, если 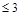 (
(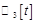 ).
).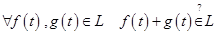 .
.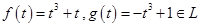 , тогда
, тогда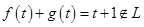 ,
,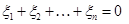 .
.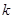 . Однако, замена на векторах
. Однако, замена на векторах 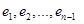 последнего нуля числом (-1) дает нам векторы из
последнего нуля числом (-1) дает нам векторы из 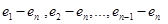
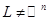 и, следовательно,
и, следовательно, 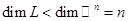 .
.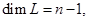
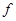 — неотрицательная квадратичная форма от
— неотрицательная квадратичная форма от 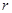 . Доказать, что все решения уравнения
. Доказать, что все решения уравнения 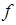 =0 образуют
=0 образуют 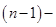 мерное линейное подпространство пространства
мерное линейное подпространство пространства 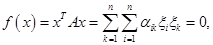
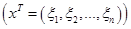 , никак не указывают на способ решения задачи.
, никак не указывают на способ решения задачи.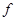 . Нормальный вид такой формы
. Нормальный вид такой формы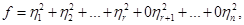 (1)
(1)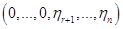 , (2)
, (2)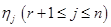 — произвольные числа из
— произвольные числа из 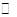 . Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть (
. Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть (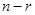 )-мерное подпространство пространства
)-мерное подпространство пространства 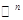 . Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга
. Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга 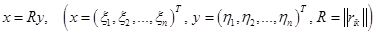 , приводящее форму
, приводящее форму 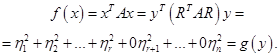
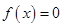 состоит из векторов
состоит из векторов 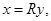 где
где 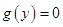 , то есть из векторов
, то есть из векторов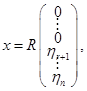
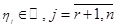 .
.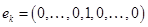 (1 на
(1 на 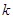 — ой позиции) и докажем, что множество
— ой позиции) и докажем, что множество 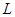 решений уравнения
решений уравнения 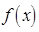 =0 есть линейная оболочка системы векторов
=0 есть линейная оболочка системы векторов 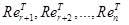
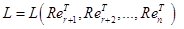 .
.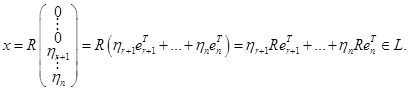
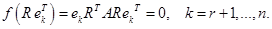
 линейно независима (проверяется непосредственно). Составляем линейную комбинацию
линейно независима (проверяется непосредственно). Составляем линейную комбинацию 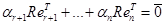 . Получаем
. Получаем 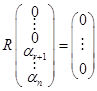 . Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица
. Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица 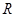 является невырожденной.
является невырожденной.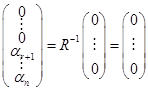 .
.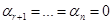 . Тем самым мы показали, что система
. Тем самым мы показали, что система 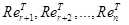 является линейно независимой. Следовательно,
является линейно независимой. Следовательно, 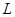 — линейное пространство (по построению) и его размерность
— линейное пространство (по построению) и его размерность 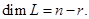
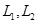 — данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление
— данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление 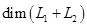 не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств
не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств 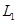 и
и 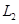 .
. 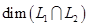 находится по формуле
находится по формуле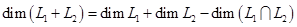 . (3)
. (3)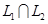 . В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй — с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).
. В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй — с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).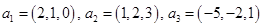 и
и 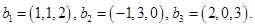
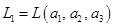 ,
, 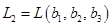 . Будем считать, что координаты векторов заданы в единичном базисе
. Будем считать, что координаты векторов заданы в единичном базисе 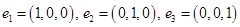 .
.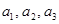 ,
, 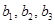 . Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.
. Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.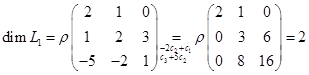 . Базис
. Базис 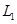 составляют
составляют 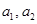 .
.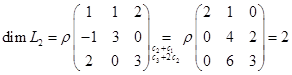 . Базис
. Базис 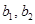 .
.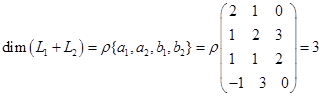 .
.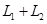 составляют
составляют 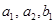 . По формуле (3) получаем
. По формуле (3) получаем 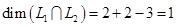 . Базис пересечения будем искать из условия
. Базис пересечения будем искать из условия 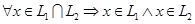 . Значит,
. Значит, 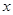 представим в виде
представим в виде 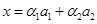 и
и 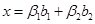 . Приравниваем правые части
. Приравниваем правые части 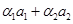
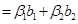 . Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда
. Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда 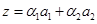
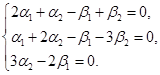
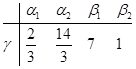
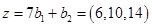 образует базис
образует базис 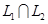 .
.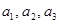 ,
, 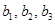 и перебрасываем наверх сначала векторы
и перебрасываем наверх сначала векторы 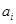 , пока это возможно (квадратиками выделены разрешающие элементы). Векторы
, пока это возможно (квадратиками выделены разрешающие элементы). Векторы 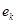 , переходящие налево, не пишем и их координаты не вычисляем.
, переходящие налево, не пишем и их координаты не вычисляем.