Найдите сумму векторов ab ad aa1 (3 видео) | Курс школьной геометрии

Смешанное, векторное и скалярное произведение векторов

Задача:

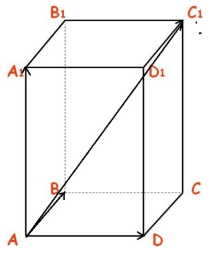
Дан параллелепипед ABCDA₁B₁C₁D₁, построен на векторах AB(4,3,0), AD(2,1,2) и AA₁(-3,-2,5).
Найти:

Решение:

а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA₁). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.

(AB AD AA₁)

4	3	0
2	1	2
-3	-2	5

20 — 18 + 0 — 0 — 30 + 16

-12

Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
V_{ABCDA₁B₁C₁D₁}=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. S_ABCD= |[AB AD]|.

[AB AD]

i	j	k
4	3	0
2	1	2

6i — 8j — 2k

Теперь найдём модуль этого вектора:

S_ABCD= \|[AB AD]\|=√	(36+64+4)	=2√(26).

[AD AA₁]

i	j	k
2	1	2
-3	-2	5

9i — 16j — k

S_ADD₁A₁= |[AD AA₁]|=√(81+256+1)=13√2.

в) Что бы найти длину высоты, проведенной из вершины A₁ на грань ABCD, используем формулу для нахождения объема параллелепипеда V=h S_ABCD. С этой формулы видим:

V
S_ABCD

12
2√(26)

6
√(26)

3√(26)
13

г) Косинус угла λ₁, между ребром AB и диагональю B₁D будем высчитывать с помощью скалярного произведения векторов

cos(λ₁)

(AB B₁D)
\|AB\| * \|B₁D\|

Координаты вектора AB мы имеем, от вектор B₁D надо найти. Для этого используем следующую формулу:
B₁D = B₁A₁ + A₁A + AD = — AB — AA₁ + AD₁ = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B₁D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B₁D:
|AB|=√(16+9+0)=5, |B₁D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B₁D, (AB B₁D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:

cos(λ₁)

4
5√(10)

2√(10)
25

д) Что бы найти cos(λ₂), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD₁A₁ мы можем взять вектор [AD AA₁], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.

cos(λ₂)

69 + (-8)(-16) + (-2)*(-1)
2√(26) * 13√(2)

46√(13)
169

Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD₁A₁.

Содержание

Правило параллелепипеда. Разложение вектора
Правило параллелепипеда
Разложение вектора по двум неколлинеарным векторам
Дан параллелепипед abcda1b1c1d1 найдите вектор ca1 + ad + d1c1 найдите вектор ab — aa1 — c1b1 найдите вектор bc1 в виде разности двух векторов, один из которых вектор d1b?
Вектор m противоположно направлен вектору b и имеет длину вектора a ?
Даны векторы x и y Найдите координаты векторов?
Найдите координаты вектора a + b если 1)вектор a , вектор b 2)вектор a, вектор b ?
Найдите скалярное произведение векторов а и b, если векторы a и b противоположно направлены и |вектора a| = 3, |вектор b| = 1?
Даны векторы а(0, 4) и b( — 3, — 2)?
Даны векторы а(3 ; 4) и b(6 ; 8)Найдите угол между этими векторами?
Даны некомпланарные векторы a, b, c?
Даны векторы ?
PABCD — пирамида, ABCD — параллелограмм, вектор PA = вектору a, вектор PB = вектору b, вектор PC = вектору с?
Дан вектор А(1 ; 4 3) Найдите абсолютную величину вектора 3а?
📹 Видео

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Правило параллелепипеда. Разложение вектора

Вы будете перенаправлены на Автор24

Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Правило параллелепипеда

Для правила сложения трех векторов рассмотрим следующую задачу.

Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$

Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.

Видео:Правило параллелепипеда для векторовСкачать

Разложение вектора по двум неколлинеарным векторам

Вспомним сначала, какие векторы называются компланарными.

Два вектора, которые параллельны одной плоскости называются компланарными.

Произвольный вектор $overrightarrow

$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow $ и $overrightarrow $ с единственными коэффициентами разложения.

Математически это можно записать следующим образом

Доказательство.

Существование: Пусть нам даны три некомпланарных вектора $overrightarrow , overrightarrow $ и $overrightarrow $. Выберем произвольную точку $O$ и построим следующие векторы:

[overrightarrow =overrightarrow, overrightarrow =overrightarrow, overrightarrow =overrightarrow и overrightarrow

=overrightarrow]

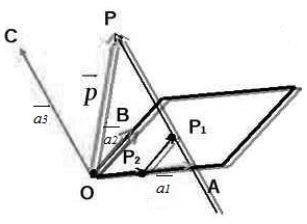
Рассмотрим следующий рисунок:

Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Тогда, получаем, что

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow

$ по векторам $overrightarrow , overrightarrow $ и $overrightarrow $:

Вычтем эти разложения друг из друга

Из этого получаем

Теорема доказана.

Видео:СУММА ВЕКТОРОВ правило треугольника Скачать

Дан параллелепипед abcda1b1c1d1 найдите вектор ca1 + ad + d1c1 найдите вектор ab — aa1 — c1b1 найдите вектор bc1 в виде разности двух векторов, один из которых вектор d1b?

Геометрия | 5 — 9 классы

Дан параллелепипед abcda1b1c1d1 найдите вектор ca1 + ad + d1c1 найдите вектор ab — aa1 — c1b1 найдите вектор bc1 в виде разности двух векторов, один из которых вектор d1b.

Ответ : а) сс1 ; б) а1с ; в) bc1 = d1c1 — d1b.

Объяснение : Правила : СУММА.

Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n — го (то есть изображается направленным отрезком, замыкающим ломаную).

Для получения вектора разности (c) = (a — b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).

Тогда : Вектор ca1 + ad + d1c1 = ca1 + a1d1 + d1c1 = сс1 (вектор ad = вектору а1d1)Вектор ab — aa1 — c1b1 = a1b — c1b1 = d1c — d1a1 = a1c (вектор a1b = вектору d1c).

Вектор bc1 = d1с1 — d1b.

Видео:Вычитание векторов. 9 класс.Скачать

Вектор m противоположно направлен вектору b и имеет длину вектора a ?

Вектор m противоположно направлен вектору b и имеет длину вектора a .

Найдите координаты вектора m.

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

Даны векторы x и y Найдите координаты векторов?

Даны векторы x и y Найдите координаты векторов.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Найдите координаты вектора a + b если 1)вектор a , вектор b 2)вектор a, вектор b ?

Найдите координаты вектора a + b если 1)вектор a , вектор b

Видео:Сложение векторов. 9 класс.Скачать

Найдите скалярное произведение векторов а и b, если векторы a и b противоположно направлены и |вектора a| = 3, |вектор b| = 1?

Найдите скалярное произведение векторов а и b, если векторы a и b противоположно направлены и |вектора a| = 3, |вектор b| = 1.

Видео:10 класс, 41 урок, Сумма нескольких векторовСкачать

Даны векторы а(0, 4) и b( — 3, — 2)?

Даны векторы а(0, 4) и b( — 3, — 2).

Найдите векторы с = 2а — b.

Видео:10 класс, 44 урок, Правило параллелепипедаСкачать

Даны векторы а(3 ; 4) и b(6 ; 8)Найдите угол между этими векторами?

Даны векторы а(3 ; 4) и b(6 ; 8)

Найдите угол между этими векторами.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Даны некомпланарные векторы a, b, c?

Даны некомпланарные векторы a, b, c.

Известно, что d = a — 2b + 3c.

Найдите разложение по векторам a, b, c вектора d1, если векторы d и d1 сонаправлены, а длина вектора d1 в три раза больше длины вектора d.

Видео:Пример 60. Найти сумму векторовСкачать

Даны векторы ?

Найдите координаты вектора p = — 1 2a + 2b — c.

Видео:№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

PABCD — пирамида, ABCD — параллелограмм, вектор PA = вектору a, вектор PB = вектору b, вектор PC = вектору с?

PABCD — пирамида, ABCD — параллелограмм, вектор PA = вектору a, вектор PB = вектору b, вектор PC = вектору с.

Выразите вектор PD = вектору х через векторы а, в, с.

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Дан вектор А(1 ; 4 3) Найдите абсолютную величину вектора 3а?

Дан вектор А(1 ; 4 3) Найдите абсолютную величину вектора 3а.

Вы зашли на страницу вопроса Дан параллелепипед abcda1b1c1d1 найдите вектор ca1 + ad + d1c1 найдите вектор ab — aa1 — c1b1 найдите вектор bc1 в виде разности двух векторов, один из которых вектор d1b?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

40 + 90 = 130 градусов Ответ : D.

1. 1)2, 4, 12, — 34, 48, 40. 2) — 3, 15, — 1, 17, — 63. 3) — 3, 12, 48, 15, — 63. 4)40, 15. 3. Р = (а + b) * 2 S = a * b 4. M = 700n.

1. По свойству острых углов треугольника угол А = 90 — 60 = 30 градусов 2. По свойству углов прямоугольного треугольника катет, лежащий против угла в 30 градусов равен половине гипотенузы = > ВС = 4 кореньиз3 3. По теореме Пифагора : AB² = AC² + BC..

Пусть х — 1 сторона, тогда х + 6 — 2 сторона. Х + х + х + х + 6 + 6 = 60 4х + 12 = 60 4х = 60 — 12 4х = 48 х = 48 / 4 х = 12 — 1 сторона, следовательно вторая сторона — 12 + 6 = 18 Ответ : 12см, 18см.

Х + х + (х + 6) + (х + 6) = 60 4х = 48 х = 12 12 + 6 = 18 ответ : 12 и 18.

Решение задачи во вложении.

Второй угол = 40° * 2 = 80° третий угол = 180 — 40 — 80 = 60°.

Сравнить углы можно двумя способами : наложением или измерением их величин. Рассмотрим, как сравнивать углы путём наложения. Дано два угла, ∠BOAи ∠COA : Чтобы выяснить, равны они или нет, наложим один угол на другой так, чтобы вершина одного угла с..

2х + 3х + 5х = 180 10х = 180 х = 18 2х = 36 3х = 54 5х = 90 Ответ : прямоугольным.

Сумма отношений равна : 2 + 3 + 5 = 10 Одна часть равна : 180 : 10 = 18° Первый угол : 2 * 18 = 36° Второй : 3 * 18 = 54° Третий : 5 * 18 = 90° Ответ : прямоугольный треугольник.