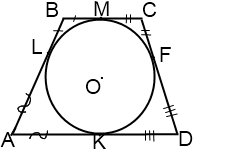
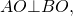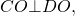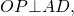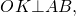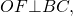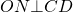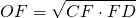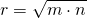Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?
1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.

2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.
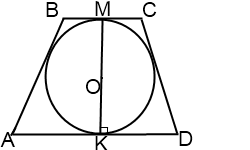
2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.
O — точка пересечения
биссектрис трапеции ABCD.
и точка O лежит на средней линии трапеции.



Видео:№710. Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.Скачать

Узнать ещё
Знание — сила. Познавательная информация
Видео:Геометрия Докажите, что диаметр окружности вписанной в равнобедренную трапецию есть среднееСкачать

В трапецию вписана окружность
Если в трапецию вписана окружность, в задаче появляется несколько путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
AB+CD=AD+BC
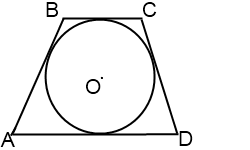
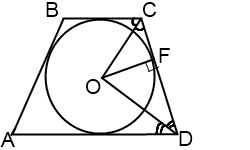
2. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что
AL=AK
BL=BM
CM=CF
DF=DK
3. Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
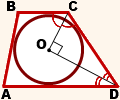
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
Рассмотрим базовую задачу.
Найти радиус вписанной в трапецию окружности, если точка касания делит боковую сторону на отрезки длиной m и n (CF=m, FD=n).
1) ∠ADC+∠BCD=180º (как сумма внутренних односторонних углов при параллельных прямых AD и BC и секущей CD);
2) так как точка O — точка пересечения биссектрис углов трапеции, то ∠ODF+∠OCF=1/2∙(∠ADC+∠BCD)=90º;
3) так как сумма углов треугольника равна 180º, то в треугольнике COD ∠COD=90º;
4) таким образом, треугольник COD прямоугольный, а OF — высота, проведенная к гипотенузе, CF и FD — проекции катета OC и OD на гипотенузу. Поскольку высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу,
Отсюда радиус вписанной в трапецию окружности выражается через длины отрезков, как которые боковая сторона делится точкой касания, как
А так как высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через длины этих отрезков:
Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать

Задача 45628 Трапеция вписана в окружность. а).
Условие
Трапеция вписана в окружность.
а) Докажите, что трапеция равнобедренная.
б) Найдите высоту трапеции, если её основания равны 14 и 40, а радиус окружности равен 25. [16п9]
Решение
а)
АВСD – трапеция, вписанная в окружность.
Если четырехугольник вписан в олружность, то суммы противолежащих углов четырехугольника равна 180
Сумма углов, прилежащих к боковой стороне трапеции равна 180 ° .
Вычитаем из первого равенства третье: ∠ С- ∠ B=0 ° ⇒
Тогда
∠ А+ ∠ В= ∠ A+ ∠ C
∠ A+ ∠ C=180 °
∠ С+ ∠ D=180 ° .
Углы при основаниях равны, трапеция [i]равнобедренная.[/i]
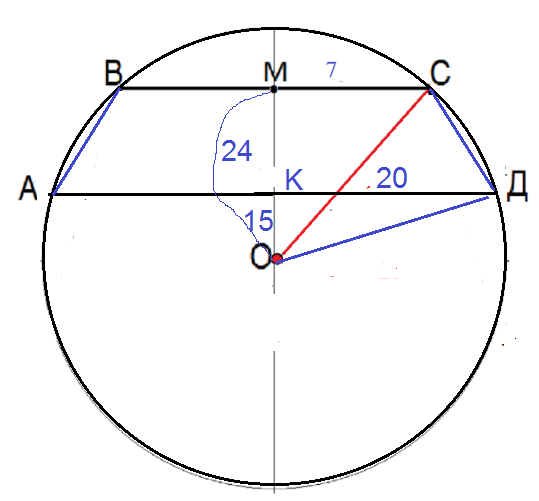
б)
Из треугольника МОС:
MO^2=25^2-7^2=(25-7)*(25+7)=18*32=36*16=6^2*4^2=(24)^2
MO=24
Из треугольника KОD:
DO^2=25^2-20^2=(25-20)*(25+20)=5*45=(15)^2
MO=15
МК=24-15=[b]9[/b] ( cм. рис.2)
О т в е т. 39 или 9 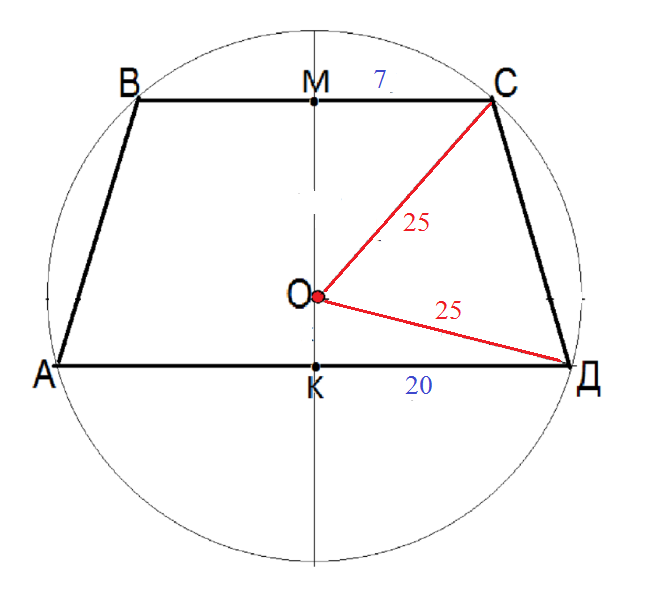
🌟 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

Где центр окружности? ТрапецияСкачать

Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

4.43.1. Планиметрия. Гордин Р.К.Скачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

№708. Докажите, что можно описать окружность: а) около любого прямоугольника; б) около любойСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Задание 25 Описанная трапецияСкачать

Окружность, вписанная в трапециюСкачать

Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

Как доказать У равнобедренной трапеции углы при основаниях равны и диагонали равныСкачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

4.39.1. Планиметрия. Гордин Р.К.Скачать

Трапеция и вписанная окружностьСкачать

Задача про трапецию, описанную около окружностиСкачать

Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делитсяСкачать